Корреляционно-регрессионный анализ

Комплекс методов статистического измерения взаимосвязей, основанный на регрессионной модели, называется корреляционно-регрессионным анализом. Первая задача состоит в определении степени влияния искажающих факторов. Второй задачей анализа является выявление на основе значительного числа наблюдений того, как меняется в среднем результативный признак в связи с изменением одного или нескольких факторов. В данной работе рассматривается влияние уровень безработицы 2-х факторных признаков:

х₁ –темпы роста (снижения) ВВП России;

х₂ –средняя заработная плата населения России.

Первая задача решается определением различных показателей тесноты связей и называется собственно корреляционным анализом. Вторая задача решается определением уравнением регрессии и носит название регрессионного анализа.

Корреляционный анализ

Первый этап – построение диаграмм распределения на основе исходных данных.

Таблица14– Динамика темпов прироста ВВП и уровня безработицы

Год	Темпы прироста ВВП, %.	Уровень безработицы, %
	-2,3	9,21
	-0,9	9,45
	-5,8	9,61
	-4,8	11,89
	-8,3	13,34
	0,8	12,81
	3,1	10,57
	4,9	9,00
	5,1	7,99
	6,2	8,68
	7,2	7,45
	6,5	7,55

На основе таблицы 14 построим диаграмму распределения и определяем существенность связи между уровнем безработицы и первым фактором–темпами прироста ВВП РФ (рис.9).

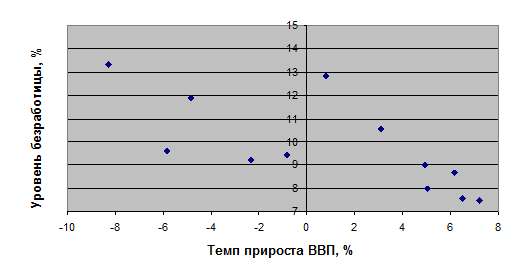
Рисунок 9 – Диаграмма распределения уровня безработицы в зависимости от темпа прироста ВВП.

Из диаграммы направленности можно сделать вывод, что связь между величинами присутствует, направление связи – обратное.

Таблица15 – Динамика средней заработной платы в РФ и уровня безработицы

Год	Средняя заработная плата РФ, тыс. руб. (в сопоставимых ценах 2014 г)	Уровень безработицы, %
	4,88	9,21
	4,44	9,45
	3,29	9,61
	3,71	11,89
	3,88	13,34
	4,20	12,81
	4,48	10,57
	4,92	9,00
	5,27	7,99
	5,90	8,68
	6,88	7,45
	7,76	7,55

На основе таблицы 15 построим диаграмму распределения и определяем существенность связи между уровнем безработицы и вторым фактором – средней заработной платой в РФ (рис.10).

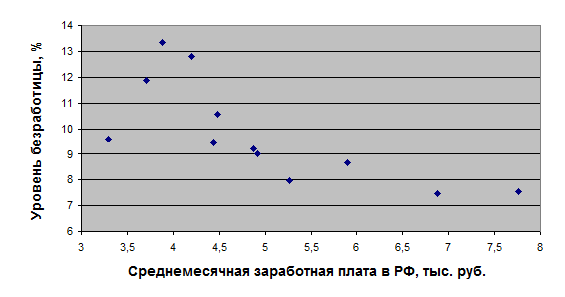
Рисунок 10 – Диаграмма распределения уровня безработицы в зависимости от среднемесячной заработной платы

Из диаграммы направленности можно сделать вывод, что связь между величинами присутствует, направление связи – обратное.

Произведем оценку существенности связи между объемом капитальных вложений и каждым из факторов на основании коэффициента корреляции. Оценка существенности связи на основе коэффициента корреляции подтверждает оценку существенности связи на основе диаграммы распределения. Коэффициент корреляции можно найти по формуле

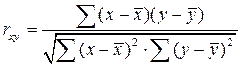(13)

где r – коэффициент корреляции;

n – число наблюдений;

На основе данных, рассчитанных в приложении Б, вычислим коэффициент корреляции между первым факторным признаком – х₁ и результативным признаком -y

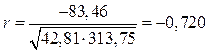
Коэффициент корреляции находиться в интервале между -0,6 и -0,8. Это говорит о том, что между уровнем безработицы и темпами прироста ВВП наблюдается сильная обратная связь.

На основе данных, рассчитанных в приложении Б, вычислим коэффициент корреляции между вторым факторным признаком – х₂ и результативным признаком -y

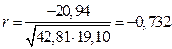
Коэффициент корреляции находиться в интервале между -0,6 и -0,8. Это говорит о том, что между уровнем безработицы и средней заработной платой наблюдается сильная обратная связь.

1. Проверка адекватности регрессионной модели (проверка значимости, существенности связи). Проверка осуществляется на основе t-критерия Стьюдента. Существенность связи на основе t-критерия Стьюдента оценивают, если выборка малая (n до 30). t-критерий Стьюдента определяют по формуле

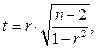(14)

где r – коэффициент корреляции;

n – число наблюдений.

Рассчитаем критерии и сравним их с теоретическими значениями для t-критерия Стьюдента.

Произведем оценку существенности связи на основеt-критерия Стьюдента между первым факторным признаком х₁ и результативным признаком

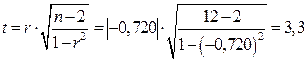
Сравним t_р с t_табл: по таблице tСтьюдента для доверительной степени вероятности Р = 0,05 и числе степеней свободы τ = n – 2 = 10, t_габл = 2,228

Так как t_р>t_табл (3,3> 2,228), значит влияние данного фактора (прирост ВВП)признается существенным.

Оценка существенности связи на основе t-критерия Стьюдента между вторым факторным признаком х₂ и результативным признаком

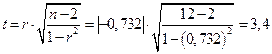
Сравним t_р с t_табл: по таблице tСтьюдента для доверительной степени вероятности Р = 0,05 и числе степеней свободы τ = n – 2 = 10, t_габл = 2,228.

Так как t_р>t_табл (3,4 > 2,262) значит влияние данного фактора (производство промышленной продукции)признается.

Регрессионный анализ

Определим зависимость между факторными признаками и результативными. При этом рассмотрим как линейные, так и криволинейные зависимости.

линейная ŷ = a + bx;

парабола ŷ = a + bx + cx²;

гипербола ŷ = a + b / x

1. Определение зависимости между результативным признаком и первым факторным признаком (прирост ВВП РФ)

По линейной форме связи:

Для нахождения аппроксимирующего уравнения по линейной форме связи решим систему уравнений, используя расчетные данные приложения В

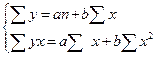(15)

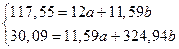
Решая систему, получаем

a = 10,05

b = – 0,266

Следовательно

y = 10,05- 0,266х₁

На основании полученного параметризованного уравнения находим ошибку аппроксимации по формуле

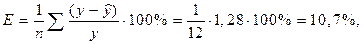
где ∑(у – ŷ) / у = 1,28 (см. приложение В)

По криволинейной форме связи (парабола):

Для нахождения аппроксимирующего уравнения по криволинейной форме связи решаем систему уравнений для параболы

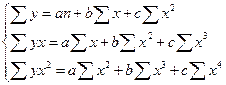(16)

Решим систему уравнений, подставив расчетные данные из приложения Г

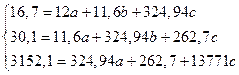
Получаем

а = 10,30

b = - 0,267

с =- 0,0089

Следовательно

y =10,30 –0,267х –0,0089х²

На основании полученного параметризованного уравнения находим ошибку аппроксимации по формуле

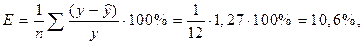
где ∑(у – y) / у = 1,27 (см. приложение Г).

По криволинейной форме связи (гиперболе):

Для нахождения аппроксимирующего уравнения по криволинейной форме связи решаем систему уравнений для гиперболы

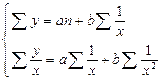(17)

Подставим расчетные данные из приложения Д в систему уравнений

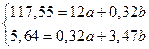
Следовательно

a = 9,78

b = 0,715

ŷ = 9,78 – 0,715 / х₁

На основании полученного параметризованного уравнения находим ошибку аппроксимации по формуле

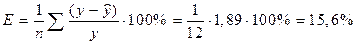
где ∑(у – y) / у = 1,89 .

По наименьшей ошибки аппроксимации отбирается та или иная модель. Наименьшая ошибка аппроксимации получается по уравнению параболы (Е_а = 10,6%), значит аппроксимирующим уравнением для оценки зависимости между результативным признаком и первым факторным признаком будет являться уравнение:

y = 10,30 – 0,267х – 0,0089х²

Так как зависимость криволинейная, определим корреляционное отношение по следующей формуле

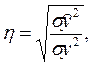(18)

где 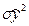– факторная дисперсия

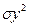– общая дисперсия

Пользуясь приложением Г вычисляем

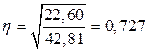
η = 0,727, следовательно, связь сильная.

Оценкапараметровнатипичностьдляаппроксимирующегопараметризованного уравнения первого факторного признака.

Для того чтобы оценить параметры уравнения на типичность нужно вычислить расчетные значения t-критерия Стьюдента.

t_a = a / m_a

t_b = b / m_b

t_с = с / m_с

где а,bиc – параметры уравнения

m_a, m_b, m_c – ошибки по параметрам

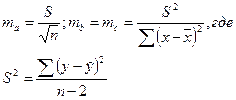(19)

Используя расчетные данные приложения Г, вычислим

S² = 20,21 : (12-2) = 2,021 => S =1,42

m_a =1,42 : 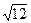= 0,41

t_a= 10,30 : 0,41 = 25,1

m_b = m_с =2,021 : 313,75 = 0,0064

t_b = 0,267 : 0,0064 = 41,7

t_с = 0,0089: 0,0064 = 1,39

Сравним расчетные значения с табличными значениями t - критерия Стьюдента, Табличное значение t - критерия Стьюдента для десяти степеней свободы и 5% уровня значимости составило

t_табл = 2,228

t_a = 25,1>2,228 => параметр а типичен

t_b = 41,7> 2,228=> параметр bтипичен

t_с = 1,39< 2,228 => параметр cнетипичен

Лишь один из параметров является не типичным, следовательно, это уравнение с небольшими допущениями можно использовать при прогнозировании уровня безработицы.

2. Определение зависимости между результативным признаком и вторым факторным признаком (среднемесячная заработная плата в РФ)

По линейной форме связи:

Для нахождения аппроксимирующего уравнения по линейной форме связи решим систему уравнений, используя расчетные данные приложения Е

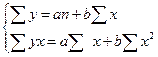(20)

Получаем

a = 15,24

b = – 1,096

Следовательно

y= 15,24 –1,096х₂

На основании полученного параметризованного уравнения находим ошибку аппроксимации по формуле

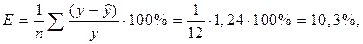
где ∑(у – ŷ) / у = 1,24

По криволинейной форме связи (парабола):

Для нахождения аппроксимирующего уравнения по криволинейной форме связи решаем систему уравнений для параболы

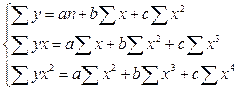(21)

Решим систему уравнений, подставив расчетные данные из приложения Ж

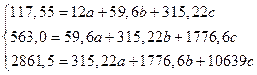
Следовательно

а = 19,05

b = -2,57

с = 0,133

y =19,05–2,57х + 0,133х²

На основании полученного параметризованного уравнения находим ошибку аппроксимации по формуле

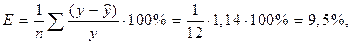
где ∑(у – y) / у = 1,14 (см. приложение Ж).

По криволинейной форме связи (гиперболе):

Для нахождения аппроксимирующего уравнения по криволинейной форме связи решаем систему уравнений для гиперболы

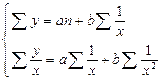(22)

Подставим расчетные данные из приложения З в систему уравнений

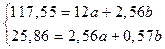
Следовательно

a = 3,9

b = 27,64

ŷ = 3,9+27,64 / х

На основании полученного параметризованного уравнения находим ошибку аппроксимации по формуле

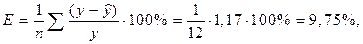
где ∑(у – y) / у = 1,17.

По наименьшей ошибки аппроксимации отбирается та или иная модель. Наименьшая ошибка аппроксимации получается по уравнению параболы (Е_а = 9,5%), значит аппроксимирующим уравнением для оценки зависимости между результативным признаком и вторым факторным признаком будет являться уравнение:

y = 19,05 – 2,57х + 0,133х²

Так как зависимость криволинейная, определим корреляционное отношение по следующей формуле

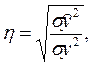(23)

где 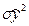– факторная дисперсия

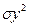– общая дисперсия

Пользуясь приложением Ж вычисляем

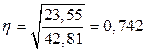
η = 0,742, следовательно, связь сильная.

Оценкапараметровнатипичностьдляаппроксимирующегопараметризованного уравнения третьего факторного признака.

Для того чтобы оценить параметры уравнения на типичность нужно вычислить расчетные значения t-критерия Стьюдента.

Используя расчетные данные приложения Ж, вычислим

S² = 19,26 : (12-2) = 1,926 => S =1,39

m_a =1,39 : 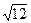= 0,401

t_a= 19,05 : 0,401 = 47,50

m_b = m_с =1,926 : 19,10 = 0,100

t_b = 2,57 : 0,100 = 25,7

t_с = 0,133 : 0,100 = 1,33

Сравним расчетные значения с табличными значениями t-критерия Стьюдента, Табличное значение t-критерия Стьюдента для десяти степеней свободы и 5% уровня значимости составило

t_табл = 2,228

t_a = 47,50>2,228 => параметр а типичен

t_b = 25,7> 2,228=> параметр bтипичен

t_с = 1,33< 2,228 => параметр cнетипичен

Лишь один из параметров является не типичным, следовательно, это уравнение с небольшими допущениями можно использовать при прогнозировании уровня безработицы.