Анализ динамики уровня безработицы

Анализ динамики явления производится на основе рядов динамики. Ряд динамики, или временной ряд – это последовательность упорядоченных во времени числовых показателей, характеризующих развитие изучаемого явления. Основная цель анализа рядов динамики состоит в изучении явления во времени.

По данным различных статистических изданий у нас имеются данные о занятости населения за период 2003 – 2014 гг. К ним относится численность экономически активного населения страны, число безработных, а также число официально зарегистрированных безработных. Ключевым показателем уровня занятости в стране является общий уровень безработицы. Именно его динамику мы и будем анализировать в данной главе. Пользуясь исходными данными, рассчитаем уровни безработицы для всего исследуемого периода.

Таблица 1 - Динамика занятости населения в РФ в 2003 – 2014 гг.

Год	Численность ЭАН, млн. чел.	Численность безработных, млн. чел.	Численность официально зарегистрированных безработных, млн. чел.	Уровень безработицы, %
	71,7	6,6	2,21	9,21
	70,9	6,7	2,31	9,45
	69,7	6,7	2,46	9,61
	68,1	8,1	2,01	11,89
	66,7	8,9	1,89	13,34
	67,9	8,7	1,48	12,81
	71,9	7,6	0,99	10,57
	71,1	6,4	1,19	9,00
	71,3	5,7	1,14	7,99
	71,4	6,2	1,57	8,68
	73,8	5,5	1,92	7,45
	74,2	5,6	1,84	7,55

Произведем анализ динамики уровня безработицы за 12 лет в период с 2003 по 2014 гг.

Каждый ряд динамики, состоит их двух элементов: показателя времени (указывает моменты или периоды времени к которому относятся приводимые статистические показатели) и уровня ряда (отображает количественную оценку развития явления во времени). Уровнем динамического ряда –y является общий уровень безработицы (коэффициент безработицы). Период времени, к которому относятся рассматриваемые уровни, равен 12 лет.

Анализ динамики начнем с проверки ряда на однородность, а также на аномальные наблюдения.

Проверка динамического ряд на однородность можно осуществить по F-критерию Фишера. Для этого необходимо разбить его на 2 совокупности:

n₁ = 8 – число наблюдений первой совокупности;

n₂ = 4 – число наблюдений второй совокупности.

9,21
9,45
9,61
11,89
13,34
12,81
10,57
9,00
7,99
8,68
7,45
7,55

Критерий Фишера находим по формуле

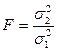(2)

где σ₁² и σ₂² – дисперсия по 1-ой и 2-ой выборкам соответственно.

Для расчет дисперсий заполним таблицу:

Таблица 2 – Расчет дисперсий выборок

Год	y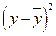
	9,21	2,33
	9,45	1,65
	9,61	1,27
	11,89	1,33
	13,34	6,79
	12,81	4,31
	10,57	0,03
	9,00	3,01
Сумма	85,88	20,71
ср. зн.	10,74
	7,99	0,01
	8,68	0,58
	7,45	0,22
	7,55	0,14
Сумма	31,67	0,94
ср. зн.	7,92

σ₁² = ∑ 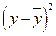/ 8 = 20,71/ 8 = 2,59

σ₂²= ∑ 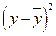/ 4 = 0,92/ 4 = 0,23

F_расч = 2,59 / 0,23 = 11,26

Данное расчетное значение сравнивают с F-критерием по таблице Фишера для уровня значимости α = 0,05 и числа степеней свободы

V₁= n₁ – k – 1 = 8 – 2 – 1 = 5

V₂= n₂ – k – 1 = 4 – 2 – 1 = 1

(где k - число выборок).

По таблице Фишера F_критич = 230,16

F_расч= 11,26 меньше F_критич = 230,16, значит данный ряд признается однородным и исследования в дальнейшем проводятся по одной выборке.

Проверим динамический ряд на аномальные наблюдения. Для этого воспользуемся критерием Граббса:

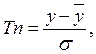(3)

где Тn – критерий Граббса

y – подозреваемое наблюдение.

σ – среднеквадратичное отклонение.

Рассчитаем критерий Граббса для всех наблюдений и представим данные в виде таблицы 3:

Таблица 3 – Расчет критерия Граббса

№ года	у	у-у	(y-y)2	Тn
	9,21	-0,59	0,34	0,310
	9,45	-0,35	0,12	0,183
	9,61	-0,19	0,03	0,098
	11,89	2,09	4,39	1,109
	13,34	3,54	12,56	1,876
	12,81	3,01	9,09	1,596
	10,57	0,77	0,60	0,410
	9,00	-0,80	0,63	0,421
	7,99	-1,81	3,26	0,956
	8,68	-1,12	1,25	0,591
	7,45	-2,35	5,50	1,242
	7,55	-2,25	5,04	1,189
Сумма	117,55		42,81
Ср. зн.	9,80

Tn_табл = 2,387 для n = 12

Сравниваем расчетные Tn с табличными; если Tn_расч>Tn_табл, то данное явление признается аномальным и исключается из рассматриваемого ряда.

В данном случае все расчетные значения меньше Tn_табл, следовательно, не являются аномальными и не исключаются из рассматриваемого ряда при дальнейшем исследовании.

В зависимости от характера отображаемого явления ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.

Абсолютный прирост (Δy) является наиболее простым показателем анализа динамики. Абсолютный прирост характеризует абсолютный размер увеличения (или уменьшения) уровня явления за определенный промежуток времени.

Если сравниваем последующий уровень с каждым предыдущим, то получаем цепные абсолютные приросты:

Δy = y_i – y_i-1, (4)

где Δy – абсолютный прирост;

y_i – текущий уровень ряда;

y_i-1 – предшествующий уровень;

i – номер уровня;

Если сравниваем каждый последующий уровень с одним уровнем, то получаем абсолютные базисные приросты:

Δy = y_i – y₀, (5)

где y₀ – базисный уровень.

Абсолютный прирост выражает абсолютную скорость роста. Используя данные таблицы 1, рассчитаем абсолютный прирост по цепной и базисной системе. Результаты представим в таблице 4:

Таблица 4 – Абсолютный прирост по цепной и базисной системе

№	год	y	ΔyЦ	ΔyБ
		9,21	–	–
		9,45	0,24	0,24
		9,61	0,16	0,40
		11,89	2,28	2,68
		13,34	1,45	4,13
		12,81	-0,53	3,60
		10,57	-2,24	1,36
		9,00	-1,57	-0,21
		7,99	-1,01	-1,22
		8,68	0,69	-0,53
		7,45	-1,23	-1,76
		7,55	0,10	-1,66
Сумма		117,55	-1,66
Ср. зн.		9,80

Для более наглядного представления данных построим график (рисунок 1).

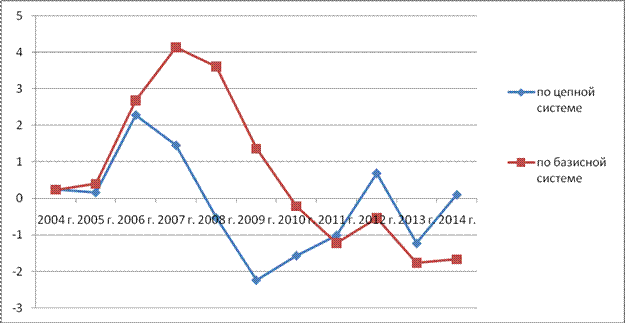
Рисунок 1 – Динамика абсолютного прироста

Анализ цепных показателей: Абсолютный прирост по цепной системе показывает на сколько единиц изменился уровень безработицы в текущем году по сравнению с предыдущим годом. Его значения были положительными в период 2004 – 2007 гг., а также в 2012 и 2014 гг. Это говорит о том, что в данные периоды уровень безработицы увеличивался. В остальные периоды уровень абсолютной прирост по цепной системе меньше нуля, это говорит о том что безработица в эти периоды времени снижалась.

Анализ базисных показателей: абсолютный прирост по базисной системе показывает, на сколько единиц изменился уровень безработицы в текущем году по сравнению с базовым 2003 годом. В 2004 – 2009 годы эта величина была больше нуля, что говорит о том, что в данном периоде безработица выросла и опустилась ниже базового уровня 2003 года лишь в 2010 году. Однако затем ее снижение продолжалось и выше базисного уровня она больше не поднималась, а чем также говорят базисные значении абсолютного прироста в период 2010 – 2014 гг.

Относительная скорость изменения уровня явления, то есть интенсивность роста, выражается коэффициентами роста и прироста, а также темпами роста и прироста.

1. Коэффициент роста – это отношение двух уровней ряда динамики. Он показывает во сколько раз сравниваемый уровень больше базисного. Коэффициент роста может быть исчислен с переменной и постоянной базой сравнения.

Если база меняется, то цепные коэффициенты роста исчисляются по формуле

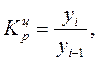(6)

где K_p – коэффициент роста.

Если база постоянная, то базисные коэффициенты роста исчисляются по формуле

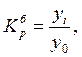(7)

Если эти величины выразить в процентах, то получим темп роста (Т_р) по цепной и базисной системам. Темп роста показывает, на сколько процентов уровень данного периода больше (или меньше) базисного уровня.

2. Коэффициенты прироста показывают относительное увеличение (уменьшение) прироста. Коэффициенты прироста рассчитываются делением абсолютного прироста на базисный абсолютный уровень или цепной

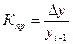( по цепной системе) (8)

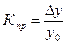(по базисной системе) (9)

Если полученные величины выразить в процентах, то получим темпы прироста (Т_пр) по цепной и базисной системам.

Используя исходные данные, рассчитаем коэффициента и темпы роста и прироста, а абсолютное значение одного процента прироста. Результаты приведем в таблице 5:

Таблица 5 – Расчет коэффициентов роста и прироста, а также темпов роста и прироста

№	Год	уi	по цепной системе	по базисной системе к 2003г
Кр(в разах)	Тр%	Кпр(в разах)	Тпр%	Кр(в разах)	Тр%	Кпр(в разах)	Тпр%
		9,21	-	-	-	-	-	-	-	-
		9,45	1,026	102,6	0,026	2,6	1,026	102,6	0,026	2,6
		9,61	1,017	101,7	0,017	1,7	1,043	104,3	0,043	4,3
		11,89	1,237	123,7	0,237	23,7	1,291	129,1	0,291	29,1
		13,34	1,122	112,2	0,122	12,2	1,448	144,8	0,448	44,8
		12,81	0,960	96,0	-0,040	-4,0	1,391	139,1	0,391	39,1
		10,57	0,825	82,5	-0,175	-17,5	1,148	114,8	0,148	14,8
		9,00	0,851	85,1	-0,149	-14,9	0,977	97,7	-0,023	-2,3
		7,99	0,888	88,8	-0,112	-11,2	0,868	86,8	-0,132	-13,2
		8,68	1,086	108,6	0,086	8,6	0,942	94,2	-0,058	-5,8
		7,45	0,858	85,8	-0,142	-14,2	0,809	80,9	-0,191	-19,1
		7,55	1,013	101,3	0,013	1,3	0,820	82,0	-0,180	-18,0
Сумма		117,55

Анализ цепных показателей: Рассматривая цепные показатели роста мы видим, что они были больше нуля в период 2004 – 2007, а также в 2012 и 2014 гг. Это говорит о том, что в эти года уровень безработицы возрастал. Наибольший прирост наблюдался в 2006 году и составил 23,7% к 2007 году. Значения остальных коэффициентов роста, меньшие единицы говорят о снижения уровня безработицы. Наибольшие снижение наблюдалось в 2009 году, в котором уровень безработицы составил 82,5% от уровня 2008года.

Анализ базисных показателей: Рассматривая базисные показатели роста мы видим, что в период 2004 – 2009 гг. значение коэффициента роста было больше единицы, что говорит о том, что уровень безработицы был больше базового уровня, причем максимальный прирост составил 44,8% от уровня 2003 года. Во второй период 2010 – 2014 гг. коэффициент роста стал меньше единицы, что свидетельствовало о снижении уровня безработицы ниже базового уровня, причем наибольшее снижение было в 2013 году, когда уровень безработицы составил 80,9% от уровня 2003 года.

Средний коэффициент роста определяют на основе средней геометрической:

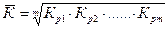(10)

гдеК – средний коэффициент роста;

К_1, К₂, К_m – коэффициенты роста (по цепной системе);

m – число коэффициентов роста.

Рассчитаем средние коэффициенты роста и прироста, для исходных данных

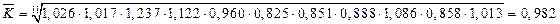
Так как произведение К₁ּК₂ּ…ּК₁₁ = y₁₂/y₁то средний коэффициент роста также можно определить по формуле:

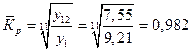
Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:

Т_р = К_р ּ100% = 0,982ּ100% = 98,2%

Средний темп роста показывает, что уменьшение уровня безработицы в среднем за 12 лет составило98,2% от предыдущего года.

Средний коэффициент прироста будет равен:

К_пр = К_р – 1 = 0,982 – 1 =– 0,018

Средний темп прироста представляет собой средний коэффициент прироста, выраженный в процентах:

Т_р = К_рּ100% = – 0,018ּ100%=– 1,8%

То есть в среднем за12 лет безработица в России уменьшалась на 1,8% в год.

При анализе рядов динамики необходимо определить общую тенденцию развития. На развитие явления во времени могут оказывать влияние различные факторы, одни из них могут формировать в рядах динамики определенную тенденцию в развитии, другие– оказывать кратковременное воздействие. Поэтому необходимо определить общую тенденцию развития.

При выявлении общей тенденции развития явления применяют различные приемы и методы выравнивания:

- укрупнение интервалов;

- сглаживание рядов динамики на основе скользящих средних;

- аналитическое выравнивание и др.

Сглаживание рядов динамики на основе скользящих средних основана на вычислении звеньев подвижной средней из такого числа уровней ряда, которая соответствует длительности наблюдаемых в ряду динамики циклов. Для этого выбираем период скольжения, равный четырем периодам. Расчет скользящих средних состоит в определении средних величин из трех уровней ряда с отбрасыванием при вычислении каждой новой средней одного уровня ряда слева и присоединением одного уровня справа.

Скользящие средние, будут вычисляется по формуле:

y_i = (y_i-1 + y_i + y_i+1 + y_i+2)/4 (11)

Чтобы получить сглаженные уровни ряда ,необходимо провести центрирование расчетных средних, определяемых как простая средняя арифметическая из 2-х рядом лежащих скользящих средних:

Сглаженные уровни будут вычисляться по формуле:

y_i= (y_i-1 + y_i)/2 (12)

Сглаживание рядов динамики отображено в таблице 6.

Таблица 6 – Расчет скользящих средних и сглаженных уровней

№	Год	y	Скользящие средние	Сглаженные уровни
		9,21	-	-
		9,45	10,04	-
		9,61	11,07	10,56
		11,89	11,91	11,49
		13,34	12,15	12,03
		12,81	11,43	11,79
		10,57	10,09	10,76
		9,00	9,06	9,58
		7,99	8,28	8,67
		8,68	7,92	8,10
		7,45	-	-
		7,55	-	-

В общем случае кривая центрированных средних выглядит более гладкой по сравнению с кривой исходных данных. Недостатком выравнивания рядов динамики на основе центрированных средних является то, что на концах динамического ряда отсутствуют данные и в результате не ясна закономерность вначале ряда и в конце.

Более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. Оно основано на допущении, что изменения в рядах динамики выражены определенным математическим законом. На основе теоретического анализа выявляется характер явления во времени и на этой основе выбирается то или иное математическое выражение типа закономерности изменения явления: линейной, степенной, показательной функции и др.

Рассматривая сглаженную линию, прлученную методом скользящих средних, мы видим, что графиик вначале идет вверх, а потом вниз, поэтому аналичическое вырвнивание будем осуществлять на основе параболы. Регрессионные функции других видов (линейная, гипербола, логарифмическая) будут заведомо иметь высокую ошибку, так как эти функцию не могут иметь одновременно и повышающийся и понижающийся участки.

Уравнение параболы имеет вид

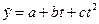
где 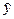- аналитически полученный уровень ряда, t – год.

Для облегчения расчетов, каждому году присвоим номера, такие чтобы сумма всех лет была равной нулю: t = -11, -9, …, 7, 9, 11.

Для нахождения аппроксимирующего уравнения решаем систему уравнений для параболы

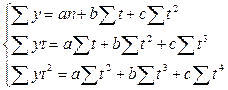
Решим систему уравнений, подставив расчетные данные из приложения А

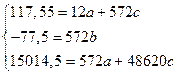
Решая систему получаем

а = 11,11; b = -0,136; с =-0,0276.

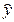=11,11 – 0,136t – 0,0276t²

На основании полученного параметризованного уравнения находим ошибку аппроксимации по формуле

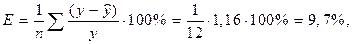
где ∑(у – y) / у = 1,16 (см. приложение А).

Ошибка аппроксимации хоть и превышает ошибку аппроксимации, однако уравнение регрессии является единственно возможным, следовательно мы будем использовать его в дальнейшем анализе с соответствующе степенью точности. В таблице 7 отражены исходные и данные, полученные аналитическим путем.

Таблица 7 – Значения регрессионной функции

Год	y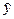
	9,21	9,27
	9,45	10,10
	9,61	10,71
	11,89	11,10
	13,34	11,27
	12,81	11,22
	10,57	10,95
	9,00	10,46
	7,99	9,74
	8,68	8,81
	7,45	7,66
	7,55	6,28

Оценим параметры уравнения на типичность/Для того чтобы оценить параметры уравнения на типичность нужно вычислить расчетные значения t - критерия Стьюдента.

t_a = a / m_a

t_b = b / m_b

t_с = с / m_с

где а,bиc – параметры уравнения

m_a, m_b, m_c – ошибки по параметрам

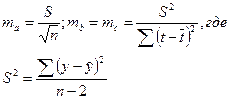
Используя расчетные данные приложения А, вычислим

S² = 16,08 : (12-2) = 1,604 => S = 1,27

m_a =1,27 : 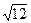= 0,367

t_a= 11,11 : 0,367 = 30,3

m_b = m_с =1,604 : 572 = 0,0028

t_b = 0,136 : 0,0028 = 48,6

t_с = 0,00278: 0,0028 = 0,99

Сравним расчетные значения с табличными значениями t-критерия Стьюдента, Табличное значение t-критерия Стьюдента для десяти степеней свободы и 5% уровня значимости составило

t_табл = 2,228

t_a =30,3 >2,228 => параметр а типичен

t_b = 48,6 >2,228=> параметр bтипичен

t_с = 0,99 <2,228 => параметр cнетипичен

На основе полученных данных строим график динамики уровня безработицы в России, а также тренд найденный методом аналитического выравнивания. (Рисунок 2).

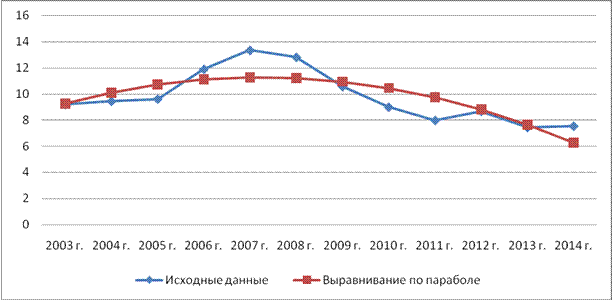
Рисунок 2 – Аналитическое выравнивание