Вычисление определенного интеграла способом подстановки

При вычислении определённого интеграла так же приходится применять различные приёмы, в том числе и способ подстановки. Подстановка в определённом интеграле делается аналогично подстановке в неопределённом интеграле, но, кроме того, для получающегося интеграла нужно находить новые пределы интегрирования.

Правило:

1) Определить, к какому табличному интегралу приводится данный интеграл;

2) Определить, какую часть подынтегральной функции необходимо заменить новой переменной, записать эту замену;

3) Вычислить дифференциал новой переменной и выразить через него оставшуюся без замены часть подынтегрального выражения;

4) Найти пределы интегрирования для новой переменной;

5) Выполнить замены под знаком интеграла;

6) Вынести за знак интеграла постоянный множитель;

7) Вычислить полученный табличный интеграл;

8) В полученное его выражение подставить вместо новой переменной сначала верхний предел интегрирования, а затем нижний, из первого результата вычесть второй.

Замечание: В отличие от неопределенного интеграла после подстановки новой переменной и замены пределов интегрировании в определённом интеграле все вычисления проводят с новой переменной и к старой переменной не возвращаются.

Пример: Вычислить:

1. ;

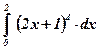Решение:

1) ;

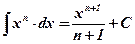2) ;

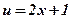3) ; ;

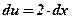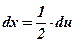4)

х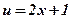

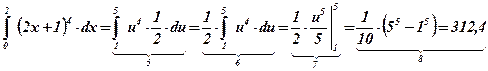
Ответ: .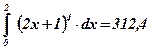

2. ;

;

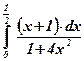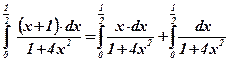1) ;

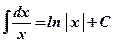2) ;

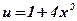3) ; ;

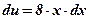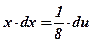4)

х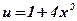

;

;

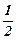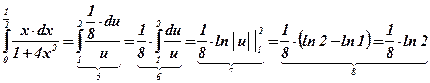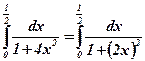1) ;

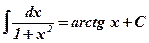2) ;

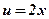3) ; ;

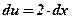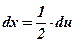4)

х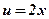

;

;

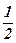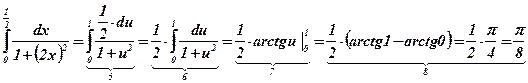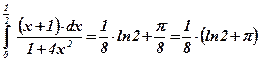Ответ: .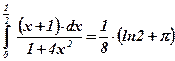

3. ;

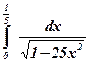1) ;

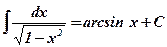2) ;

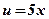3) ; ;

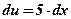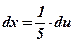х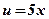

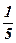4)

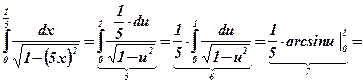
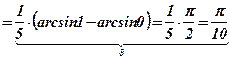
Ответ: .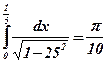

Упражнения: Вычислить определённые интегралы:

1) 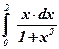;	2) 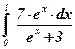;	3) ;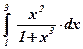
4) 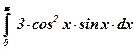;	5) 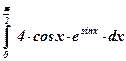;	6) ;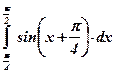
7) 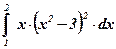;	8) 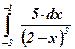;	9) ;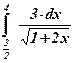
10) 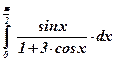;	11) 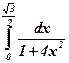;	12) ;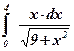
13) 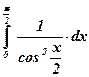;	14) 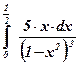;	15) ;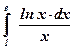
16) 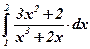;	17) 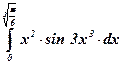;	18) ;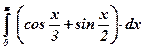
19) 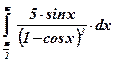;	20) 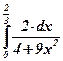;	21) ;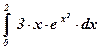
22) 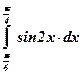;	23) 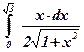;	24) ;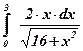
25) 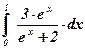;	26) 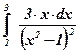;	27) .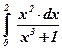

Ответы:

1) 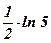;	2) 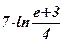;	3) 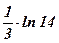;	4) 2;	5) 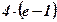;	6) ;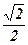
7) 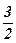;	8) 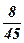;	9) 3;	10) 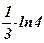;	11) 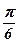;	12) 2;
13) 2;	14) 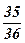;	15) 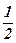;	16) 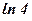;	17) 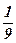;	18) ;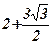
19) 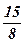;	20) 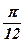;	21) 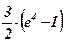;	22) 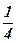;	23) 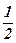;	24) 2;
25) 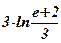;	26) 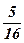;	27) ;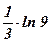

Площадь криволинейной трапеции. Геометрический смысл определенного интеграла

Определение: Криволинейной трапецией называется фигура, ограниченная осью абсцисс ( 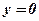), двумя прямыми, параллельными оси ординат ( 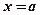, 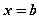), непрерывной и неотрицательной функцией 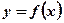при рассматриваемых значениях аргумента.

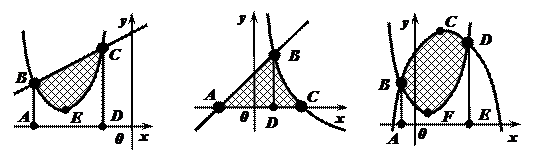
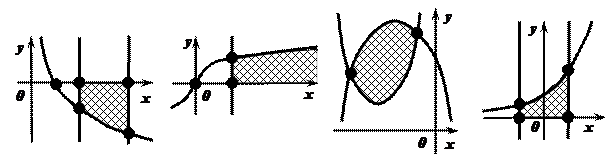Задача №1. Является ли фигура криволинейной трапецией?

Рис. 1. Рис. 2. Рис. 3. Рис. 4.

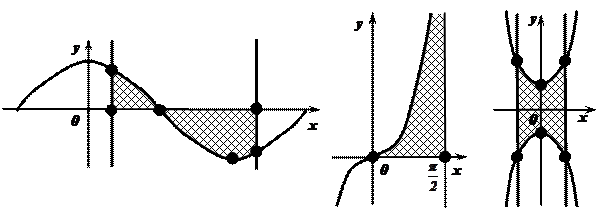
Рис. 5. Рис. 6. Рис. 7.

Решение:

1. Фигура (Рис.1.) не является криволинейной трапецией, так как функция, её ограничивающая принимает отрицательные значения при рассматриваемых значениях аргумента.
2. Фигура (Рис.2.) не является криволинейной трапецией, так как она не ограничена справа прямой, параллельной оси ординат.
3. Фигура (Рис.3.) не является криволинейной трапецией, так как она не ограничена осью абсцисс.
4. Фигура (Рис.4.) является криволинейной трапецией, так как она ограничена осью абсцисс, двумя прямыми, параллельными оси ординат, непрерывной и неотрицательной функцией 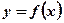при рассматриваемых значениях аргумента.
5. Фигура (Рис.5.) не является криволинейной трапецией, так как функция, её ограничивающая принимает неотрицательные и отрицательные значения при рассматриваемых значениях аргумента.
6. Фигура (Рис.6.) не является криволинейной трапецией, так как функция, её ограничивающая не является непрерывной при рассматриваемых значениях аргумента.
7. Фигура (Рис.7.) не является криволинейной трапецией, так как она не ограничена осью абсцисс.

Задача №2. Выразить площади фигур через площади криволинейных трапеций.

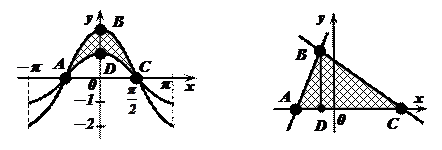Рис. 1. Рис. 2. Рис. 3.

Рис. 4. Рис. 5.

Решение:

1. Площадь фигуры BCE (Рис.1.) равна разности площадей криволинейных трапеций ABCD u ABECD: .
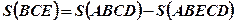2. Площадь фигуры ABC (Рис.2.) равна сумме площадей криволинейных трапеций ABD u BCD: .
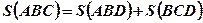3. Площадь фигуры BCDF (Рис.3.) равна разности площадей криволинейных трапеций ABCDЕ u ABFDE: .
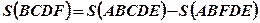4. Площадь фигуры ABCD (Рис.4.) равна разности площадей криволинейных трапеций ABC u ADC: .
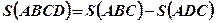5. Площадь фигуры ABC (Рис.5.) равна сумме площадей криволинейных трапеций ABD u BCD: .

Задача №3. Найти концы интервала, на котором построена фигура, ограниченная функциями:

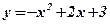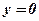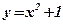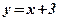1) ; ; 2) ; ; 3) ; .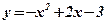

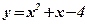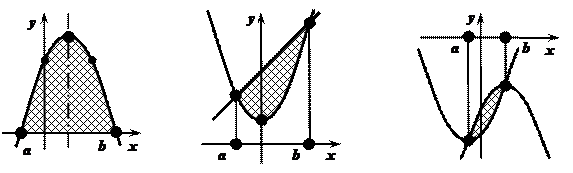Рис. 1. Рис. 2. Рис. 3.

Решение:

1) Концами интервала a u b, на котором построена данная криволинейная трапеция, являются абсциссы точек пересечения параболы 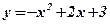и оси абсцисс 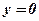. Решим способом подстановки систему уравнений:

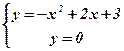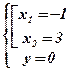Û Û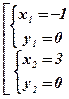

;

; ;

; ; ; ;

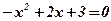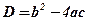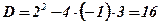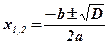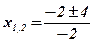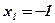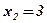Ответ: ; .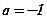

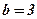2) Концами интервала a u b, на котором построена данная фигура, являются абсциссы точек пересечения параболы 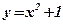и прямой 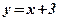. Решим способом подстановки систему уравнений:

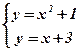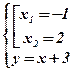Û Û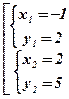

; ; ;

; ; ;

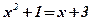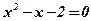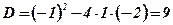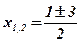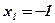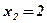Ответ: ; .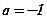

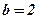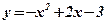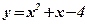3) Концами интервала a u b, на котором построена данная фигура, являются абсциссы точек пересечения парабол и . Решим способом подстановки систему уравнений:

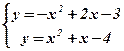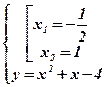Û Û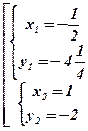

; ; ;

; ; ;

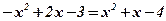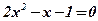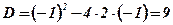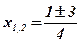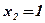Ответ: ; .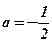

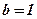Упражнения:

1. Построить фигуру, ограниченную функциями 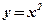, , 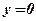, 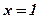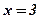. Является ли фигура криволинейной трапецией? Найти концы интервала, на котором построена фигура.
2. Построить фигуру, ограниченную функциями 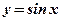, , 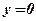, 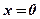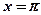. Является ли фигура криволинейной трапецией? Найти концы интервала, на котором построена фигура.

Построим криволинейную трапецию Р₀М₀МР, ограниченную функцией 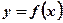, положительной и возрастающей при рассматриваемых значениях аргумента .

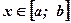От чего зависит площадь криволинейной трапеции Р₀М₀МР?

1. Площадь криволинейной трапеции Р₀М₀МР зависит от длины отрезка 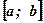, на котором она построена: чем больше длина отрезка 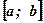, тем больше площадь криволинейной трапеции Р₀М₀МР .

2. Площадь криволинейной трапеции Р₀М₀МР зависит от вида ограничивающей её функции .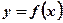

Вывод: Площадь криволинейной трапеции, ограниченной непрерывной и неотрицательной функцией 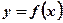на отрезке 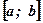оси абсцисс равна определённому интегралу в пределах от а до b от функции .

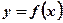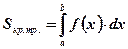
Вывод: Геометрический смысл определённого интеграла состоит в том, что определённый интеграл в пределах от а до b от непрерывной и неотрицательной функции 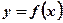равен площади криволинейной трапеции, ограниченной функцией 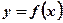на отрезке 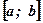оси абсцисс.

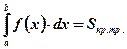
Пример:

1. Вычислить площадь криволинейной трапеции, построенной на отрезке 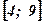оси абсцисс и ограниченной функцией 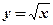. Сделать чертёж.

Решение:

Воспользуемся формулой площади криволинейной трапеции:

.

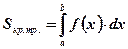
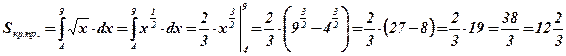Ответ: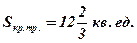

1. Вычислить площадь криволинейной трапеции, построенной на отрезке 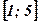оси абсцисс и ограниченной функцией 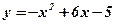. Сделать чертёж.

Решение:

;

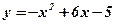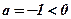- ветви направлены вниз;

; ;

; ;

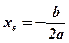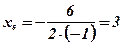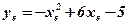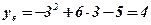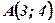- вершина параболы;

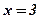- ось симметрии параболы;

х
у				- 5

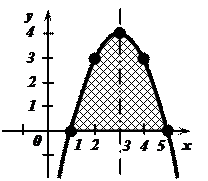
Концы интервала, на котором построена данная криволинейная трапеция, являются абсциссами точек пересечения параболы 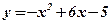и оси абсцисс 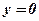. Решим способом подстановки систему уравнений:

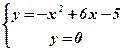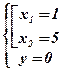Û Û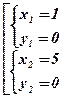

; ; ;

; ; ; ;

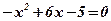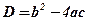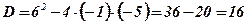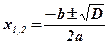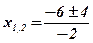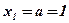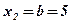Воспользуемся формулой площади криволинейной трапеции: .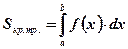

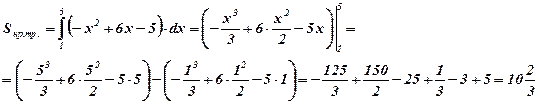
Ответ: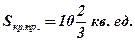

Упражнения: