Удовлетворяющее условиям

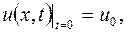(5.9)

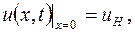
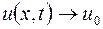при 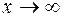. (5.10)

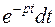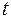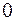Решение. Умножим каждый член уравнения (5.8) на и проинтегрируем по от до 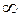. В результате получим операторное уравнение относительно аргумента :

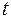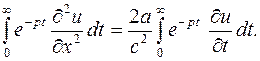(5.11)

При фиксированном 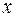интеграл 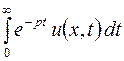есть лапласово изображение функций 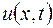, которое обозначим 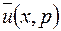. Итак, в наших обозначениях

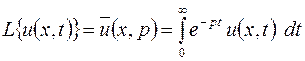(5.12)

С учетом (5.12) интеграл в левой части уравнения (5.11) можно представить в виде

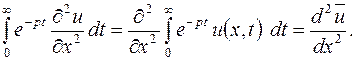(5.13)

К интегралу в правой части (5.11) применим формулу интегрирования по частям. Тогда

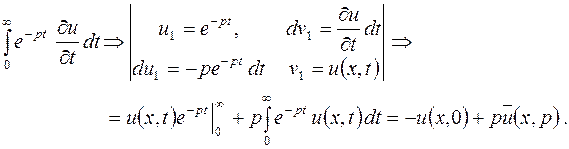
С учетом условия (5.9) окончательно получаем

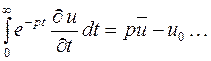(5.14)

Подставляя (5.13) и (5.14) в (5.8), будем иметь обыкновенное дифференциальное уравнение второго порядка по аргументу

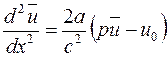, (5.15)

Которое следует решить при условиях

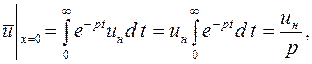(5.16)

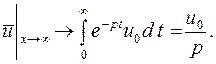(5.17)

Применяя теорию интегрирования линейных уравнений второго порядка, согласно которой общее решение неоднородного уравнения складывается из общего решения однородного уравнения и частного решения неоднородного уравнения, найдем, что общее решение уравнения (5.15) имеет вид

,

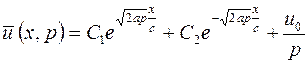где 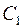и 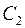– произвольные постоянные. Определим их из условий (5.16), (5.17). Из ограниченности функци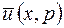и при 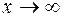в силу условия (5,17) следует, что 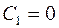. Из условия (5.16)

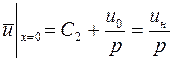
получаем .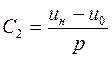

Итак, .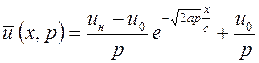

По данному изображению 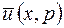определим оригинал –

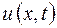Искомое решение задачи. По формуле (18) из таблицы соответствий

Устанавливаем, что

,

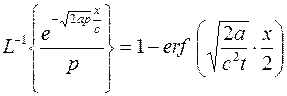где 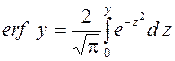табулированная функция, так называемый интеграл ошибок, а .

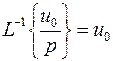Следовательно,

.

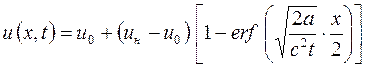6. УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

	Найти изображения функци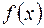и и	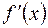Ответы
	;	;
	;	;
	;
	;	;
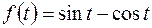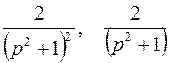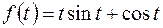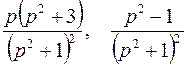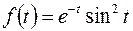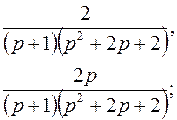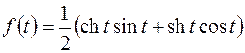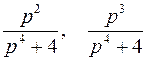Найти изображение функций	Ответы
	;	;
	;	;
	;	;
	;	;
	;	;
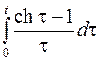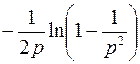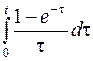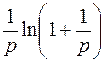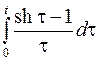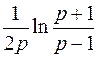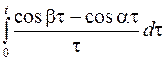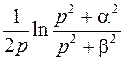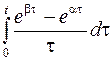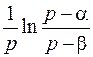Найти оригинал по заданному изображению и сделать график	Ответы
	;
	;
	;
	;
	;
	;	;
	;	;
	;	;
	;
	;	;
	;	;
	;	;
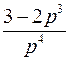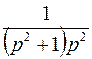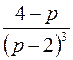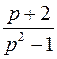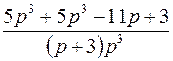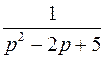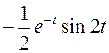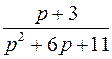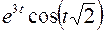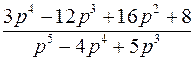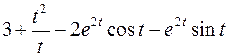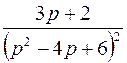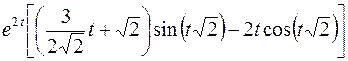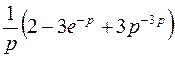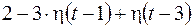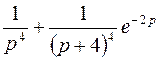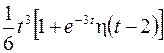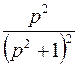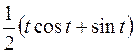Используя теорему умножения изображений и формулу Дюамеля, найти оригиналы для следующих изображений:	Ответы
	;	;
	;	;
	;	;
	;	;
	;	;
	;	;
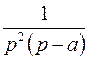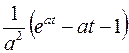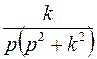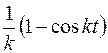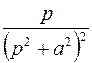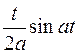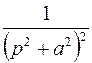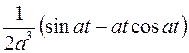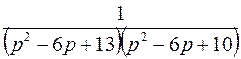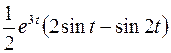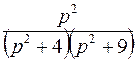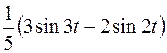Используя первую теорему разложения, найти оригинал по его изображению	Ответы
	;	;
	;	;
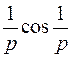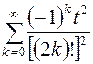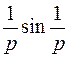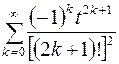Используя вторую теорему разложения, найти оригинал для следующих изображений	Ответы
	;	;
	;	;
	;	;
	;	;
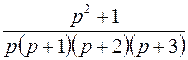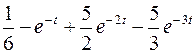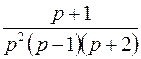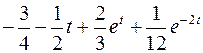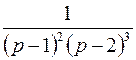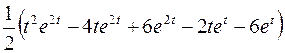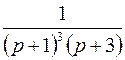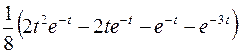Решить дифференциальные уравнения при указанных начальных условиях:	Ответ
		;
		;
	, ;	;
	, , ;	;
	, ;	;
	, ;	;
	, , ;
	, ;
	, ;	;
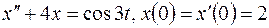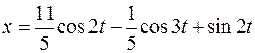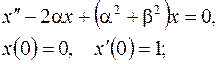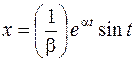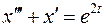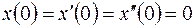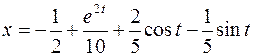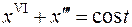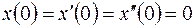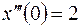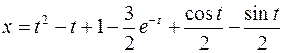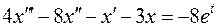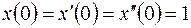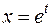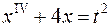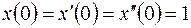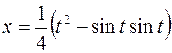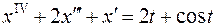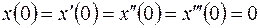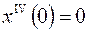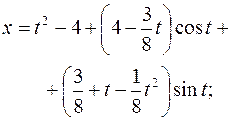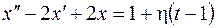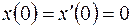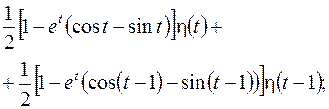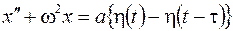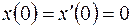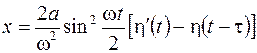Решить систему дифференциальных уравнений	Ответы
	;
	, , ;
	;
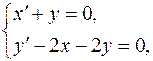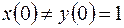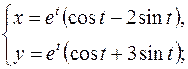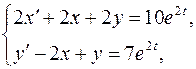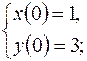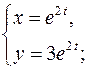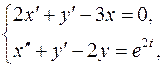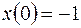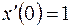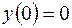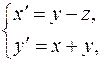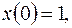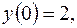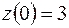Применив интеграл Дюамеля, решить дифференциальные уравнения
	, ;
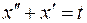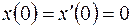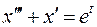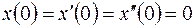Проинтегрировать ЛДУ при нулевых начальных условиях:	Ответ
	,

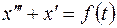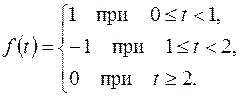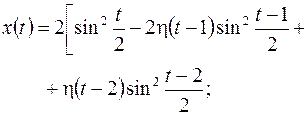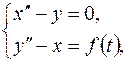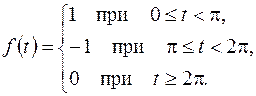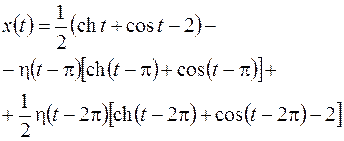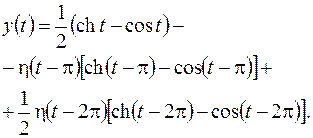Список литературы

1. Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. – М: Наука,1968.

2. Болгов В.А. и др. Сборник задач по математике. Специальные разделы математического анализа. / Под. ред. А.В. Ефимова, Б.П. Демидовича – М.: Наука, 1981.

3. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Наука, 1989. -464 с.

4. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. ч.II. – М.: Высшая школа, 1980.

5. Жевержеев В.Ф., Кальницкий Л.А. Сапогов Н.А. Специальный курс высшей математики для втузов. – М.: Высшая школа, 1970.

6. Краснов М.А., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. – М.: Наука, 1981.

7. Кожевников Н.И., Краснощекова Т.И., Шишкин Н.Е. Ряды и интегралы Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. – М.: Наука, 1964. -184 с.

8. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. – М.: Наука, 1970.

9. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. – М.: Наука, 1979. -320 с.

Приложение

Таблица оригиналов и изображений

	Оригинал	Изображение	Примечание

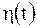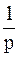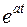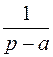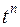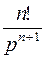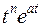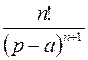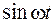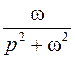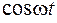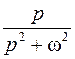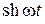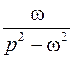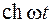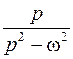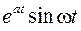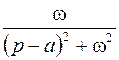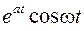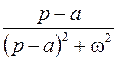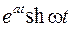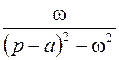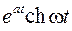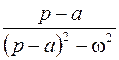Продолжение прил.

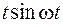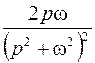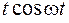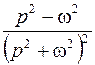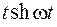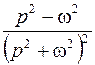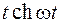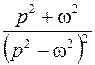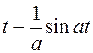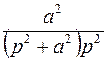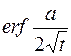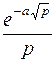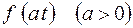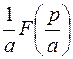			теорема подобия
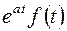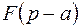			теорема смещения
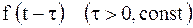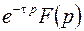			теорема запаздывания
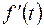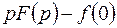			дифференцирование оригинала
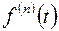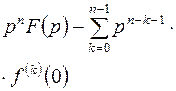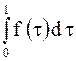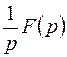			интегрирование оригинала

Окончание прил.

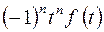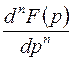			дифференцирование изображения
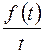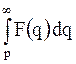			интегрирование изображения
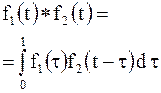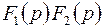			умножение изображений

* Условие дифференцируемости , можно заменить более удобным для пользования условием непрерывности частных производных этих функций по обеим переменным и .

*) Заметим, что если дробь неправильная то стремится к нулю при и, следовательно, не может быть изображением.

Заметимчто если дробь неправильная ( П стремится к нулю при р-*сч-> и, следовательно, не может быть изображением.