Непрерывность функций

Лекция №1. Пределы. Непрерывность функций.

Цели:ознакомить обучающихся с определением предела, с замечательными пределами, научить вычислять пределы.

Определение пределов.

Пусть функция 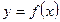определена в некоторой окрестности точки 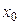, кроме, быть может, самой точки .

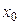Определение. Число А называется пределом функции в точке 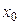(или при 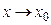), если для любого положительного 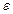найдется такое положительное число 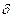, что для всех 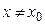, удовлетворяющих неравенству 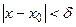, выполняется неравенство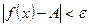

Записывают .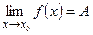

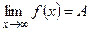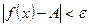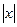Аналогично , если при >N.

Условно записывают 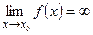, если 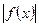>M при 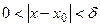, где М – произвольное положительное число. В этом случае функция называется бесконечно большой при .

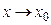Если 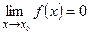, то функция 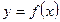называется бесконечно малой при .

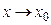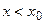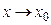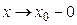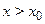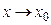Если и , то употребляют запись ; если и , то употребляют запись .

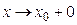Числа 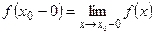и 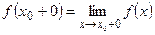называются соответственно левым и правым пределом функции 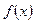в точке .

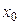Для существования предела функци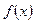и при 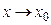необходимо и достаточно, чтобы .

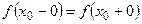2. Теоремы о пределах:

Теорема 1. 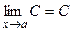, где .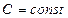

Следующие теоремы справедливы при предположении, что функци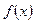и и 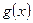имеют конечные пределы при .

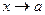Теорема 2.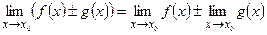

Теорема 3.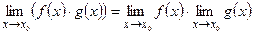

Следствие 1. Постоянный множитель можно выносить за знак предела:

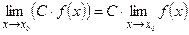
Следствие 2.Предел степени с натуральным показателем равен той же степени предела:

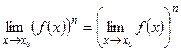
Теорема 4. .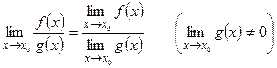

3. Замечательные пределы:

Первый замечательный предел:

.

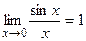Второй замечательный предел (число е = 2,718…):

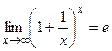или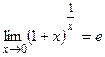

При решении примеров полезно иметь в виду следующие равенства:

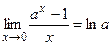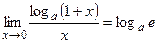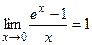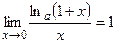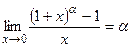Вычисление пределов

Предел элементарной функци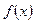и при 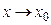, которое входит в область ее определения равен частному значению функции при 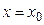, т. е.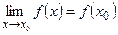

Пример №1.

Вычислить предел: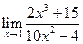

Решение: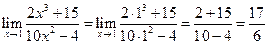

В курсе математического анализа рассматриваются неопределенности вида .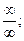

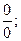
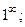
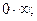
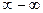Чтобы раскрыть неопределенность вида 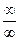, заданную отношением двух многочленов, надо числитель и знаменатель разделить на самую высокую, входящую в них степень х, а затем перейти к пределу.

Пример №2.

Вычислить предел: .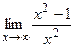

Решение: .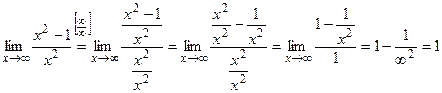

Чтобы раскрыть неопределенность вида 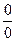, заданную отношением двух многочленов, надо в числителе и знаменателе выделить критический множитель (т.е. множитель, равный 0 при предельном значении х) и сократить на него

Пример №3.

Вычислить предел: .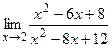

Решение: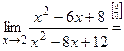

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби

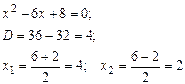
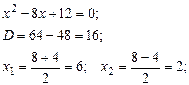
Тогда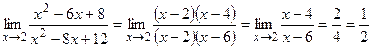

Пример №4.

Вычислить предел: .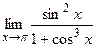

Решение:

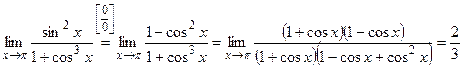
Чтобы раскрыть неопределенность вида 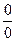, в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.

Пример №5.

Вычислить предел: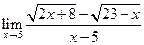

Решение:

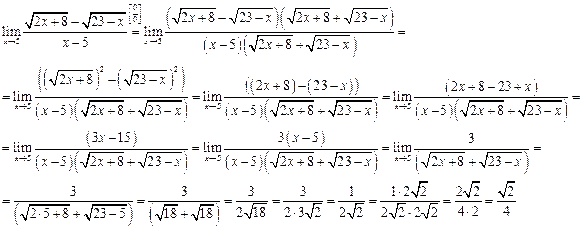
Неопределенность 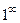раскрывается, используя второй замечательный предел.

Пример №6.

Вычислить предел: .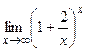

Решение: Обозначим 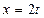, очевидно, 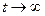при 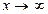. Имеем

.

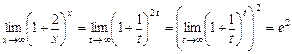Пример №7.

Вычислить предел: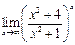

Решение:

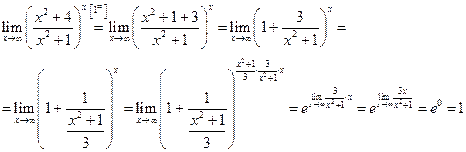
Пример №8.

Вычислить предел: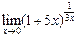

Решение: .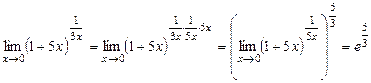

Пример №9.

Вычислить предел: .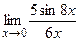

Решение: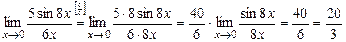

Непрерывность функций.

Функция 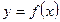называется непрерывной в точке 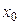, если:

1) функция определена в точке 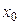и в ее окрестности;

2) существует предел 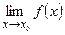(это подразумевает существование и равенство односторонних пределов 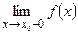и )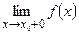

3) этот предел равен значению функции в точке 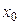, т.е. .

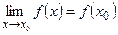Обозначая 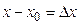(приращение аргумента) и 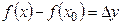(приращение функции), условие непрерывности можно записать так: 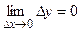, т.е. функция 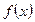непрерывна в точке 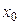тогда и только тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Если функция непрерывна в каждой точке некоторой области (интервала, сегмента и т.п.), то она называется непрерывной в этой области.

Точка 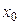, принадлежащая области определения или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается условие непрерывности функции.

Если существуют конечные пределы 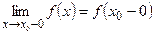и 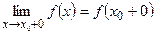, причем не все три числа 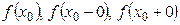равны между собой, то 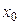называется точкой разрыва I рода.

Точки разрыва I рода подразделяются в свою очередь, на точки устранимого разрыва (когда 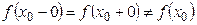, т.е. когда левый и правый пределы в точке 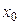равны между собой, но не равны значению функции в этой точке) и на точки скачка (когда 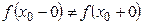,т.е когда левый и правый пределы функции в точке 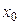различны); в последнем случае разность 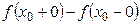называется скачком функции в точке .

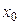Точки разрыва не являющиеся точками разрыва I рода, называются точками разрыва I I рода. В точках разрыва II рода не существует хотя бы один из односторонних пределов.

Сумма и произведение конечного числа непрерывных функций есть функция непрерывная. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, где делитель не равен нулю.

Пример №1.

Исследовать функцию 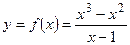на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.

Решение:

1) Под прицел попадает единственная точка 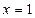, в которой функция не определена.

2) Вычислим односторонние пределы:

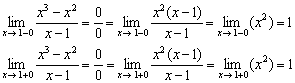
Односторонние пределы конечны и равны.

Таким образом, в точке 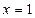функция терпит устранимый разрыв.

Как выглядит график данной функции?

Хочется провести упрощение 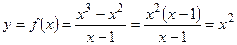, и вроде бы получается обычная парабола. НО исходная функция не определена в точке 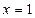, поэтому обязательна следующая оговорка: 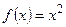, если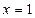
Выполним чертёж:

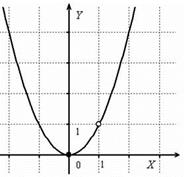
Ответ: функция непрерывна на всей числовой прямой кроме точки 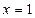, в которой она терпит устранимый разрыв.

Пример №2.

Показать, что при 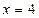функция 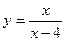имеет разрыв.

Решение:

Вычислим односторонние пределы

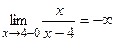
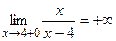
Таким образом, функция при 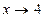не имеет ни левого , ни правого конечного предела. Следовательно, 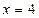является точкой разрыва II рода

Пример №3

Исследовать функцию на непрерывность и построить график функции

.

Решение: очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства 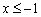значение 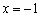принадлежит прямой 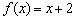(зелёная точка), и в силу неравенство 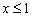значение 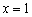принадлежит параболе 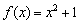(красная точка):

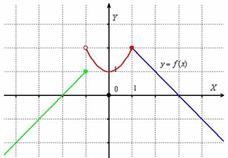
Оформим решение. Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:

I) Исследуем на непрерывность точку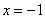

1) 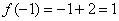– функция определена в данной точке.

2) Найдём односторонние пределы:

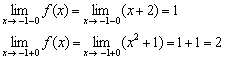
Односторонние пределы конечны и различны, значит, функция 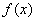терпит разрыв 1-го рода со скачком в точке .

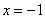Вычислим скачок разрыва как разность правого и левого пределов:
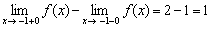, то есть, график рванул на одну единицу вверх.

II) Исследуем на непрерывность точку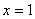

1) 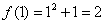– функция определена в данной точке.

2) Найдём односторонние пределы:

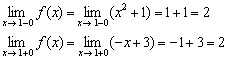
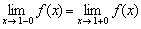– односторонние пределы конечны и равны, значит, существует общий предел.

3) 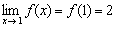– предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция 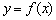непрерывна в точке 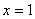по определению непрерывности функции в точке.

На завершающем этапе переносим чертёж на чистовик, после чего ставим финальный аккорд:

Ответ: функция непрерывна на всей числовой прямой, кроме точки 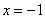, в которой она терпит разрыв первого рода со скачком.