С помощью функции Хевисайда она может быть записана одним выражением
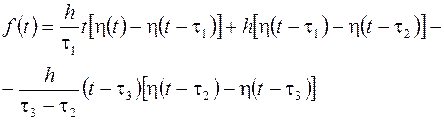 .
.
Для определения изображения  функции
функции  преобразуем ее к виду, допускающему применение теоремы запаздывания к соответствию
преобразуем ее к виду, допускающему применение теоремы запаздывания к соответствию 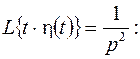
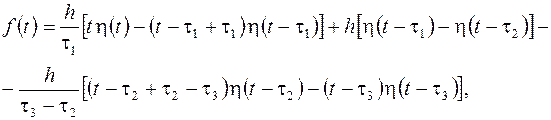
Откуда получаем


Тогда

Или
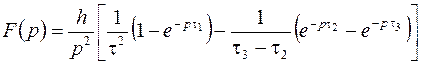 .
.
Так как 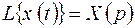 и
и 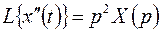 (в силу нулевых начальных условий), то операторное уравнение имеет вид
(в силу нулевых начальных условий), то операторное уравнение имеет вид
 ,
,
Откуда находим
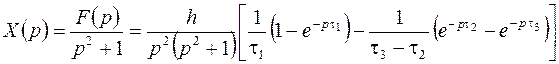 .
.
Воспользовавшись таблицей соответствий (формула (17)), найдем
 .
.
Оригиналы остальных слагаемых изображения 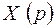 ,отличающихся от первого слагаемого множителем вида
,отличающихся от первого слагаемого множителем вида 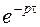 , определяются с помощью теоремы запаздывания, а именно
, определяются с помощью теоремы запаздывания, а именно
 .
.
Таким образом, окончательный вид решения задачи Коши следующий:
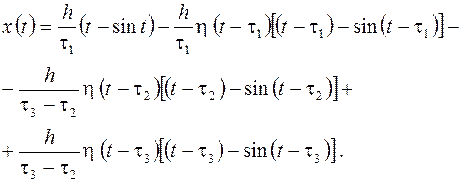
Хотя операционный метод был проиллюстрирован на примере уравнений второго порядка, ясно, что упрощение вычислительной работы благодаря его применению становится существенным при решении дифференциальных уравнений порядка более высокого, чем два.
5.2. Решение систем дифференциальных уравнений
В большей мере преимущества преобразования Лапласа проявляются при решении систем линейных дифференциальных уравнений, причем оно принципиально не отличается от решения одного дифференциального уравнения. Каждое уравнение данной системы заменяется соответствующим операторным уравнением, тогда вместо системы дифференциальных уравнений образуется система линейных алгебраических уравнений относительно изображений искомых функций. Такие системы изящно решаются по правилу Крамера. Затем от найденных изображений переходят к искомым функциям. Операционный метод интегрирования систем дифференциальных уравнений покажем на примере.
Пример 5.3. Решить систему уравнений

при начальных условиях  .
.
Решение. Положим 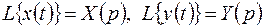 . С учетом начальных условий найдем
. С учетом начальных условий найдем 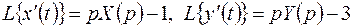 .
.
Внося в уравнения системы изображения вместо функций, приходим к следующей системе операторных уравнений:
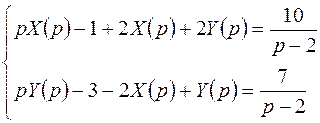 .
.
Приведем систему алгебраических уравнений к нормальной форме:
 .
.
Теперь по формулам Крамара найдем

Переходя от изображений 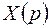 и
и 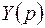 к их оригиналам, получаем искомые решения
к их оригиналам, получаем искомые решения
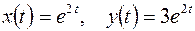
Решение линейных дифференциальных уравнений
В частных производных
Операционный метод используется и при решении линейных дифференциальных уравнений в частных производных при определенных краевых условиях. Применение этого метода к уравнению в частных производных, где искомая функция является функцией двух переменных, приводит к обыкновенному дифференциальному уравнению, что, естественно, упрощает решение задачи. Применение операционного метода для интегрирования линейных уравнений в частных производных покажем на примере уравнения второго порядка относительно функции двух переменных, не обсуждая здесь физический смысл уравнения и условий, наложенных на искомую функцию.
Пример 5.4. В области 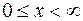 ,
,  найти решение
найти решение 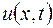 уравнения
уравнения
 (5.8)
(5.8)
