Взаимное пересечение плоскостей общего положения

Если плоскости общего положения заданы следами, то естественно искать точки, определяющие прямую пересечения плоскостей, в точках пересечения одноименных следов плоскостей: прямая, проходящая через эти точки, является общей для обеих плоскостей, т.е. их линией пересечения (рис. 16)

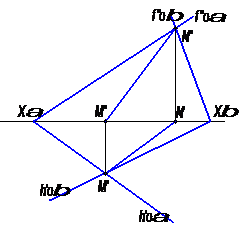
Рис. 16

Поэтому для построения проекций линии пересечения плоскостей α и β

(рис. 16) надо:

1) найти точку M′ в пересечении следов h_oα и h_oβ и точку N′′ в пересечении f_оα и f_оβ, а по ним – проекции M′′ и N′;

2) построить проекции искомой прямой M′′N′′ и M′N′.

Общий прием построения линии пересечения двух плоскостей заключается в том, что вводят вспомогательную плоскость и строят линии пересечения вспомогательной плоскости с двумя заданными, а в пересечении построенных линий находят общую точку двух плоскостей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной плоскости.

На рисунке 17 дан пример построения линии пересечения двух плоскостей общего положения. Одна из плоскостей α задана двумя пересекающимися прямыми, а другая β – двумя параллельными прямыми.

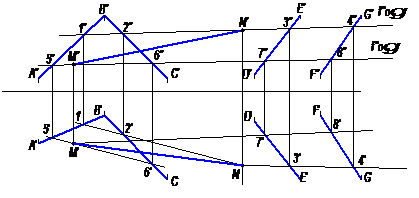
Рис. 17

Для нахождения общих точек взяты две вспомогательные фронтально-проецирующие плоскости γ₁ и γ ₂ пересекающие каждую из плоскостей α и β. При пересечении плоскостей α и β с плоскостью γ₁ образуются прямые (1-2) и (3-4), расположенные в плоскости γ₁. В своем пересечении они определяют первую точку линии пересечения плоскостей α и β – точку N. Далее, с введением плоскости γ₂, получены, в ее пересечении с плоскостями α и β, прямые (5-6) и (7-8). Эти прямые, расположенные в плоскости γ₂, в своем пересечении определяют вторую точку, общую для плоскостей α и β – точку М. Строят точки M и N, сначала получив проекции N′, M′, а затем находят на следах f_оγ1, f_оγ2 проекции M′′, N′′. Этим определяются проекции M′N′ и M′′N′′ искомой прямой пересечения плоскостей

α и β.

Построить линию пересечения двух плоскостей можно по точкам пересечения прямых линий одной плоскости с другой плоскостью.

Следовательно, надо уметь строить точку пересечения прямой линии с плоскостью общего положения.

На рисунке 18 дан пример построения линии пересечения двух треугольников АВС и DEF.

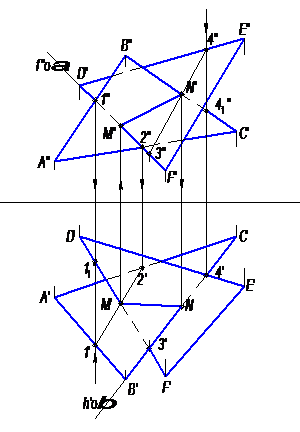
Рис.18

Прямая MN построена по точкам пересечения стороны DF с треугольником АВС и стороны ВС с треугольником DFE. Вспомогательная фронтально-проецирующая плоскость α, проведенная через DF, пересекает треугольник АВС по прямой (1-2), дающей в пересечении с D′F′ точку М, являющуюся точкой пересечения прямой DF и треугольника АВС.

Проведенная через сторону ВС вспомогательная горизонтально-проецирующая плоскость β пересекает треугольник DEF по прямой (3-4), дающей в пересечении с ВС точку N, являющуюся точкой пересечения прямой ВС и треугольника DEF. Соединив одноименные проекции точек M и N получают искомую линию пересечения – MN. Далее определяется видимость сторон треугольников в проекциях по конкурирующим точкам.

Например, с помощью фронтально-конкурирующих точек 1 и 1₁, которые соответственно расположены на сторонах АВ и DF. Точка 1 расположена к наблюдателю ближе, чем точка 1₁, поэтому она закрывает собой эту точку и на фронтальной проекции точка – 1₁′′ будет невидимой и, следовательно, фронтальная проекция стороны DF так же невидимая на отрезке (1′′M′′).

С помощью горизонтально-конкурирующих точек 4 и 4₁, расположенных соответственно на сторонах DE и ВС определяется видимость их горизонтальных проекций. Точка 4 расположена выше, чем точка 4₁, поэтому горизонтальная проекция точки 4 будет видимой, а точки 4₁ невидимой. Следовательно, горизонтальная проекция стороны DE, на которой лежит точка 4, будет видимой, а горизонтальная проекция стороны ВС на отрезке (N′4′) – невидимой и т.д.