Принятые обозначения и символы
Обозначения
1. Точки в пространстве – прописными буквами латинского алфавита А ,В, С,…, а также цифрами – 1, 2, 3…
2. Линии в пространстве – строчными буквами латинского алфавита a, b, c,…
3. Плоскости – строчными буквами греческого алфавита 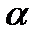 ,
, 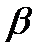 , …
, …
4. П1 ,П2 ,П3 – основные плоскости проекций.
5. П4 ,П5 – дополнительные плоскости проекций.
6. Ox, Oy, Oz – оси проекций.
7. 0 – начало координат.
8. Проекции точек: на горизонтальную плоскость П1 – А′, В′, С′,…;
на фронтальную плоскость П2 – А′′, В′′, С′′,…;
на профильную плоскость П3 – А′′′, В′′′, С′′′;
на дополнительную плоскость П4 – АIV, ВIV, СIV, …..
9. Обозначение плоскостей заданных следами:
горизонтальный след плоскости 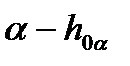 ;
;
фронтальный след плоскости 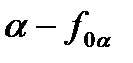 ;
;
профильный след плоскости 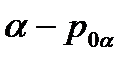 .
.
10. Для проецирующих плоскостей:
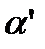 – горизонтально - проецирующая плоскость;
– горизонтально - проецирующая плоскость;
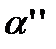 – фронтально - проецирующая плоскость;
– фронтально - проецирующая плоскость;
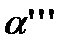 – профильно - проецирующая плоскость.
– профильно - проецирующая плоскость.
11. Точки схода следов плоскости – прописными буквами X, Y, Z с индексами соответствующей плоскости: X 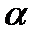 , Y
, Y 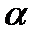 , Z
, Z 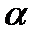 .
.
Символы
 = – равны, результат действия
= – равны, результат действия

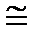 – конгруэнтны (совмещены)
– конгруэнтны (совмещены)

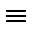 – конкурирование; тождественное совпадение
– конкурирование; тождественное совпадение

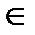 – инцидентность
– инцидентность

 – пересечение
– пересечение

 – объединение; соединение
– объединение; соединение

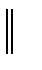 – параллельность
– параллельность

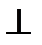 – перпендикулярность
– перпендикулярность
 . – скрещивание
. – скрещивание

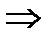 – импликация; логическое следствие (следовательно, поэтому)
– импликация; логическое следствие (следовательно, поэтому)
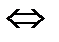 – эквивалентность (что тоже самое)
– эквивалентность (что тоже самое)
Латинский и греческий алфавит
Латинский алфавит
Буква Название Буква Название
Aa а Nn эн
Bb бэ Oo о
Cc цэ Pp пэ
Dd дэ Qq ку
Ee е Rr эр
Ff эф Ss эс
Gg же Tt тэ
Hh ха (аш) Uu у
Ii и Vv вэ
Jj йот Ww дубль-вэ
Kk ка Xx икс
Ll эль Yy игрек
Mm эм Zz зет
Греческий алфавит
Буква Название Буква Название
А 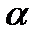 альфа N
альфа N 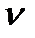 ню
ню
В 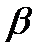 бэта
бэта 
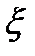 кси
кси
Г 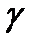 гамма O
гамма O 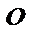 омирон
омирон
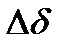 дельтаП
дельтаП 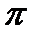 пи
пи
Е 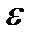 эпсилонP
эпсилонP 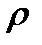 ро
ро
Z 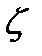 дзета
дзета 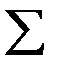
 сигма
сигма
Н 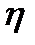 этаT
этаT 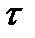 тау
тау

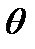 тэтаY
тэтаY 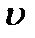 ипсилон
ипсилон
I 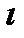 йотаФ
йотаФ 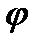 фи
фи
K 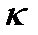 каппаФ
каппаФ 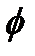 хи
хи
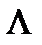
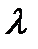 лямбда
лямбда 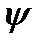
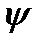 пси
пси
M 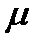 мю
мю 
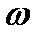 омега
омега
Блок 1
Начертательная геометрия
Лабораторная работа №1
Чертеж Монжа. Координатный метод задания точки на чертеже. Конкурирующие точки. Прямая линия. Положение прямой линии относительно плоскостей проекций. Взаимное положение двух прямых
Цель:изучение методики построения эпюра Монжа, построения конкурирующих точек и определения видимости посредством таких точек, методики решения задач на нахождение следов прямой, на взаимное положение прямых.
1.1. По пространственному изображению точек А, B, C, D, E (рис. 51), построить их эпюры. Определить положение данных точек в пространстве.
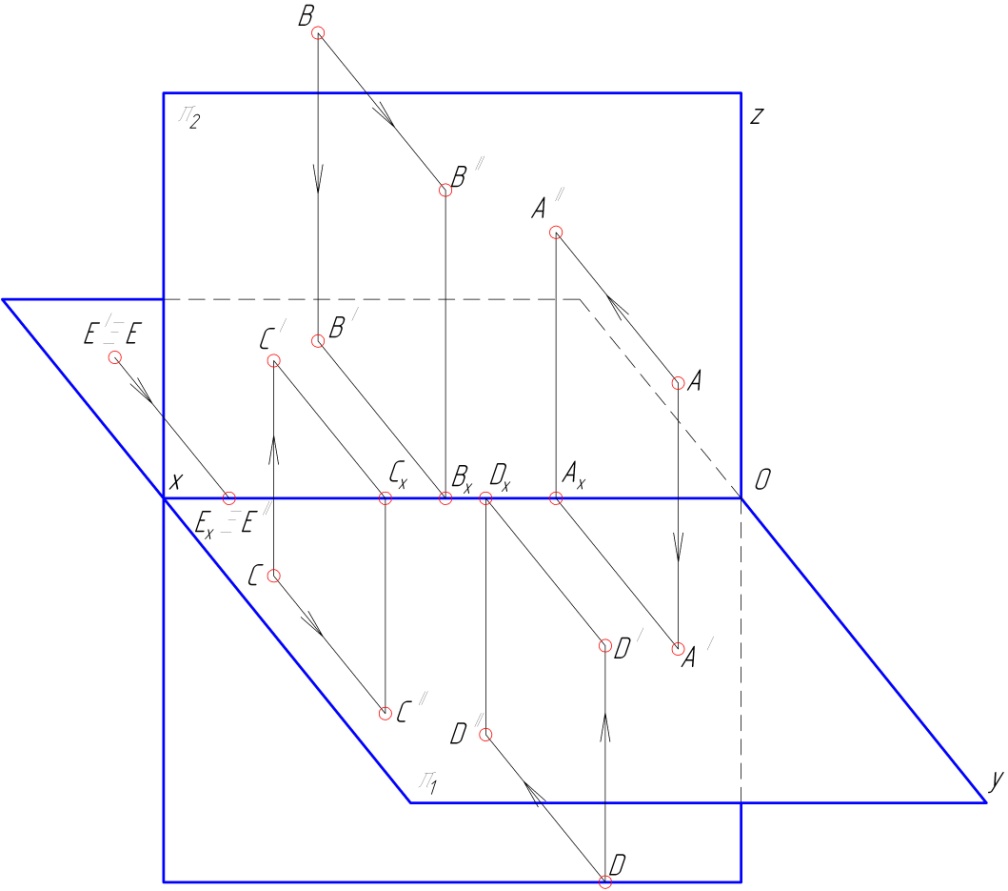
Рис. 51
1.2. Относительно точки А построить горизонтально-конкурирующую видимую точку С, относительно точки В горизонтально-конкурирующую невидимую точку D. Относительно точки М построить фронтально-конкурирующую видимую точку Е, относительно точки N построить фронтально-конкурирующую невидимую точку К (рис. 52). Построить пространственные изображения данных точек.
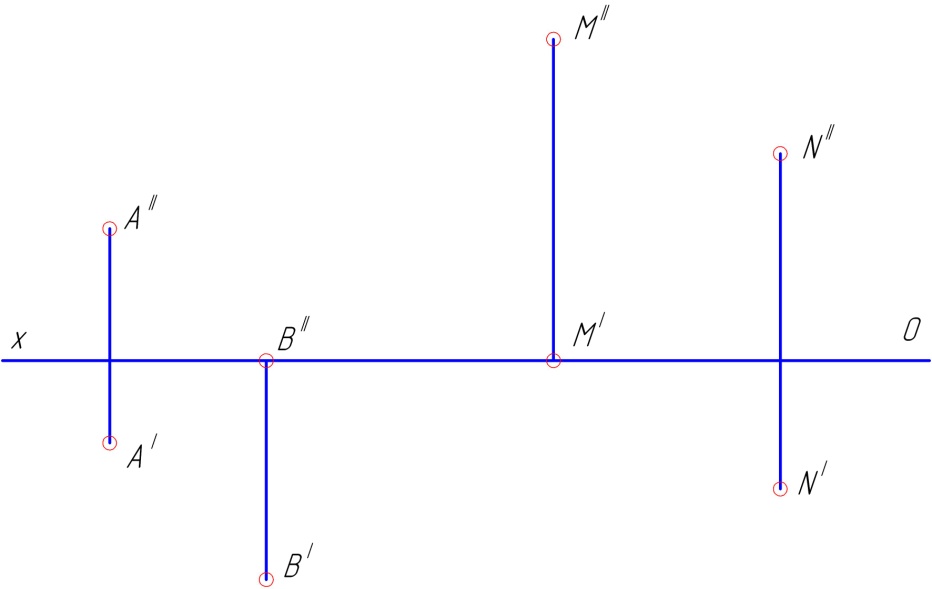
Рис. 52
1.3. Построить следы прямых (рис. 53). Определить положение данных прямых относительно плоскостей проекций, дать их наименование.
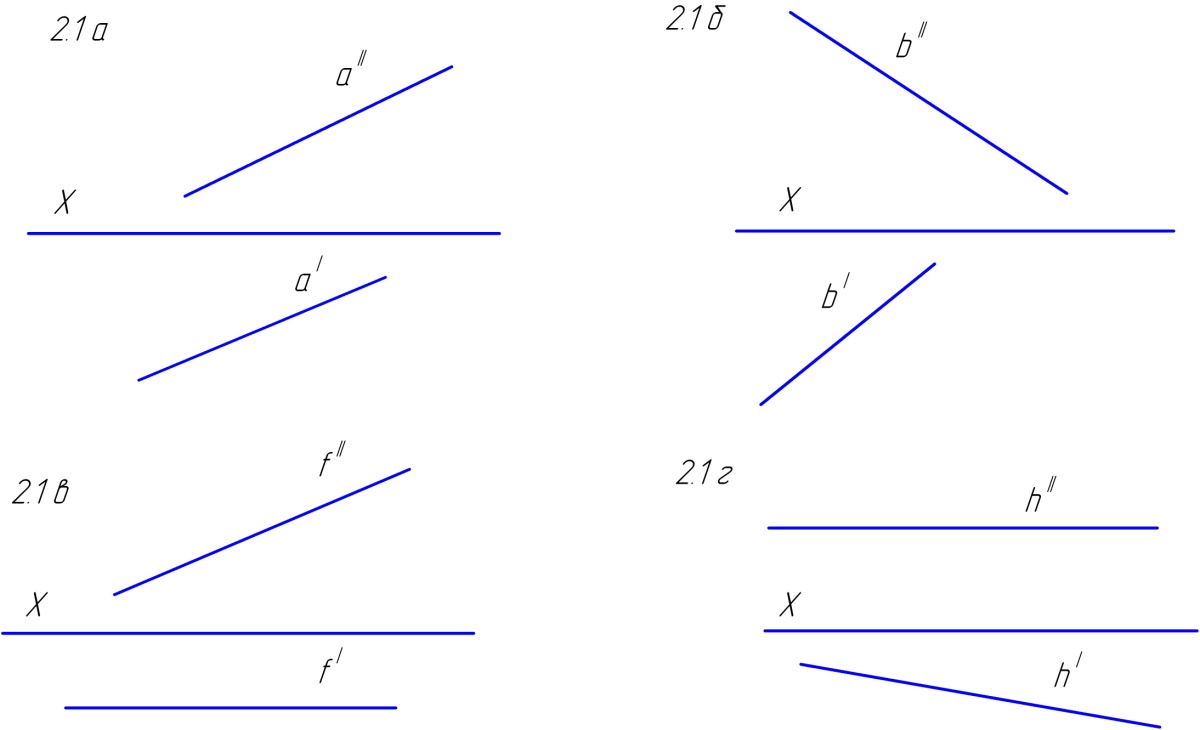
Рис. 53
1.4.а) Построить отрезок прямой [АВ] ║ П1; [AB]; П2=300; [AB]=50 мм;
б) Построить отрезок прямой [CE] ║ П2; [CE]; П1=300; [CE]=40 мм;
1.5. а) Построить прямую а ║ р, причем М  а (рис. 54);
а (рис. 54);
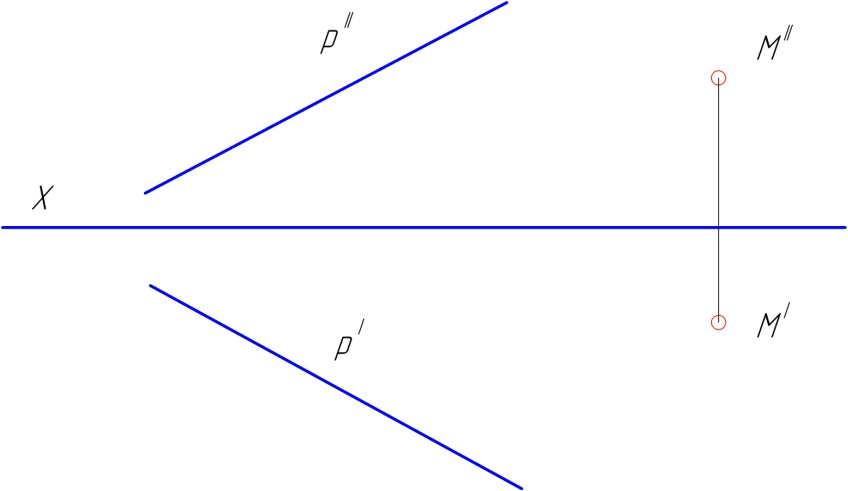
Рис. 54
1.5. б) Построить прямую α ║ с, причем р ∩ α (рис. 55).
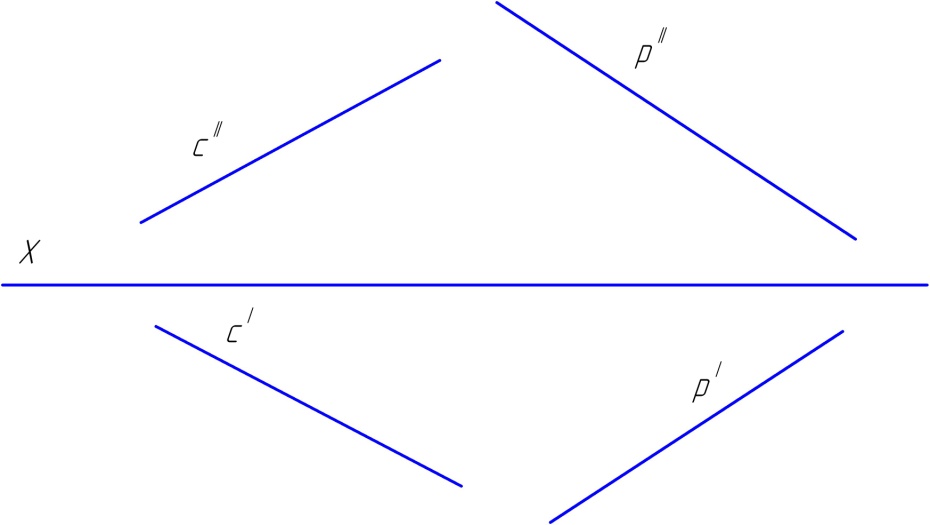
Рис. 55
Задачи для самостоятельного решения
Задача 1
Тема «Точка»
Построить эпюр и наглядное изображение точек по заданным координатам (таб. 3). Определить положение точек в пространстве.
Таблица 3
| A | B | C | D | |||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | |
| -50 | -10 | |||||||||||
| -10 | -20 | -10 | -20 | |||||||||
| -30 | -10 | -20 | -10 | -20 | ||||||||
| -10 | -20 | -10 | -20 | -60 | ||||||||
| -10 | -10 | -30 | -15 | |||||||||
| -10 | -10 | -30 | -10 | |||||||||
| -60 | -20 | -30 | -20 | |||||||||
| -10 | -20 | -10 | -50 | -40 | ||||||||
| -20 | -10 | -10 | -15 | |||||||||
| -15 | -20 | -10 | ||||||||||
| -10 | -15 | |||||||||||
| -50 | -40 | -20 | -30 | -10 | -10 | -30 | ||||||
| -20 | -10 | -15 | ||||||||||
| -40 | -15 | -15 | ||||||||||
| -15 | -10 | -20 | -10 | -15 | -20 | -40 | ||||||
| -10 | -10 | -10 | ||||||||||
| -30 | -40 | -30 | ||||||||||
| -60 | -30 | -20 | -40 | |||||||||
| -15 | -10 | -20 | -30 | -10 | ||||||||
| -70 | -20 | -10 | -20 | |||||||||
| -10 | -10 | -15 | -20 | |||||||||
| -10 | -15 | -30 | -10 | |||||||||
| -10 | -30 | -15 | -40 | -10 | ||||||||
| -10 | -10 | -20 | -30 | -10 | ||||||||
| -15 | -40 | -60 | ||||||||||
| -40 | -15 | -10 | ||||||||||
| -40 | -10 | -10 | ||||||||||
| -10 | -30 | -10 | ||||||||||
| -15 | -20 | -20 | ||||||||||
| -30 | -30 | -10 | -40 | -15 |
Задача 2
Тема «Прямая»
1-10. Определить характер каждой прямой, ее положение в пространстве.
Построить пространственное изображение прямых.
11-16. Через точку А провести отрезок прямой длинной 30 мм, соблюдая
условия:
11, 14. [AB] ║ П1, с П2 образует угол 450;
12, 15. [AD] ║ П2, с П1 образует угол 300;
13, 16, [AK] ║ П2, с П1 образует угол 600.
17-21. Методом прямоугольного треугольника найти истинную длину отрезка АВ и углы его наклона к П1 и к П2.
22-25. Отрезок прямой АВ разделить в отношении: 4:1, 1:3, 1:2, 2:3.
26-30. Построить следы прямой, указать через какие четверти пространства она проходит.
Используя данные на рис. 56.
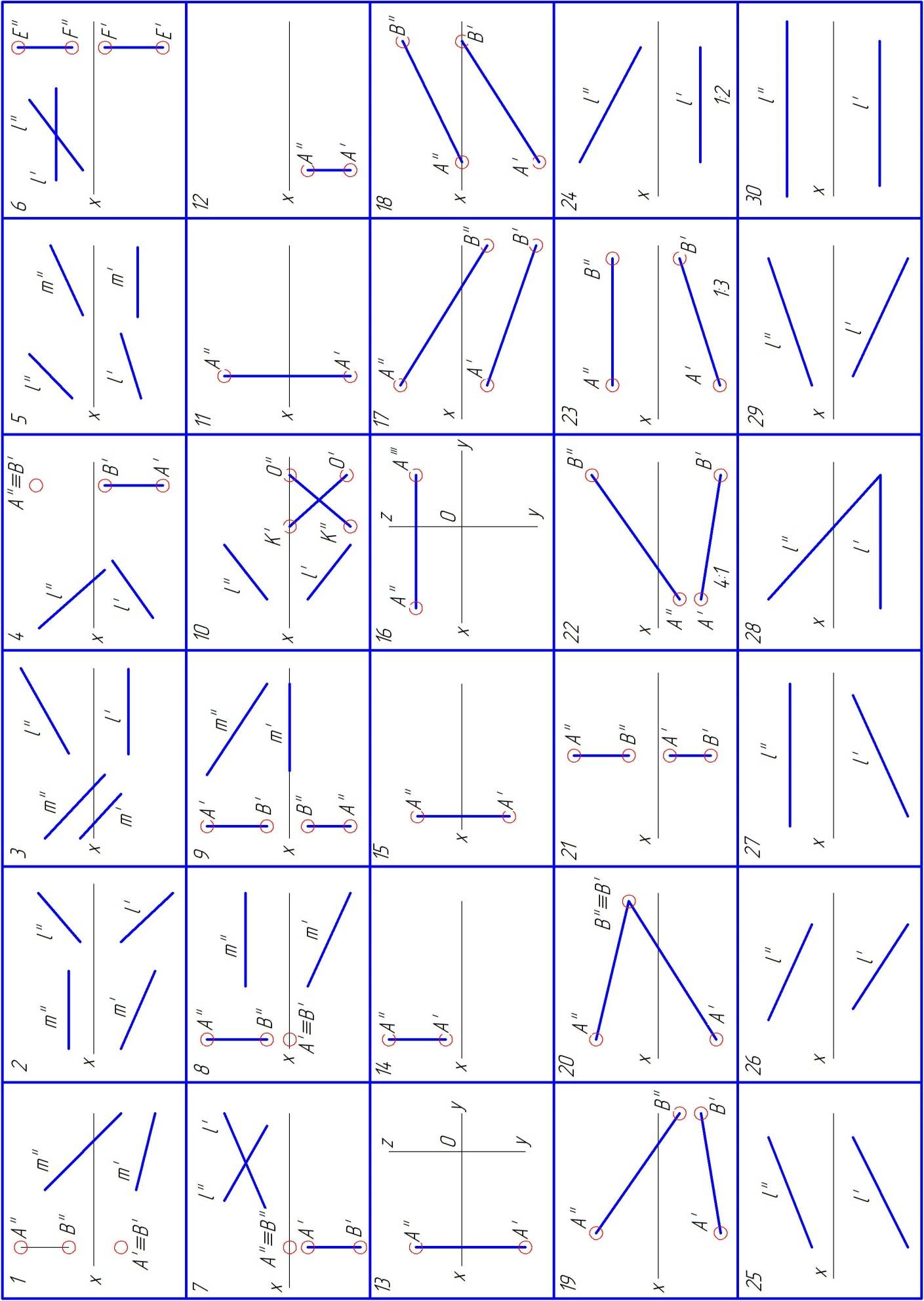 Рис. 56 Данные к задаче 2 на тему прямая
Рис. 56 Данные к задаче 2 на тему прямая
Контрольные вопросы
1. Что такое эпюр?
2. Какими координатами задаётся горизонтальная (фронтальная) проекция точк ?
3. Каким четвертям, какие знаки соответствуют?
4. Что такое конкурирующие точки? дать определение.
5. Какую прямую называют: а) прямой общего положения; б) прямой уровня; в) проецирующей прямой?
6. Что является характерным для прямых частного положения: а) прямых уровня (горизонтали, фронтали, профильной прямой); б) для проецирующих прямых?
7. Какие проекции прямой вполне определяют её положение в пространстве?
8. Какое положение относительно друг друга могут занимать две прямые?
Лабораторная работа №2
Плоскость. Способы задания плоскости на чертеже. Точка в плоскости. Взаимное положение прямой и плоскости. Поверхность. Гранные поверхности, поверхности вращения. Задание на чертеже. Принадлежность точки поверхности.
Цель:изучение классификации плоскостей и способов задания плоскости при решении типовых задач, методики решения задач на принадлежность точки и прямой плоскости, на взаимное пересечение прямой и плоскости, задание поверхностей на чертеже, принадлежность точки поверхности.
2.1.
а Построить горизонтально-проецирующую плоскость под углом 300 к фронтальной плоскости проекций.
б Построить фронтально-проецирующую плоскость под углом 600 к горизонтальной плоскости проекций.
2.2. Построить недостающие проекции прямых, принадлежащих плоскости (рис. 57).
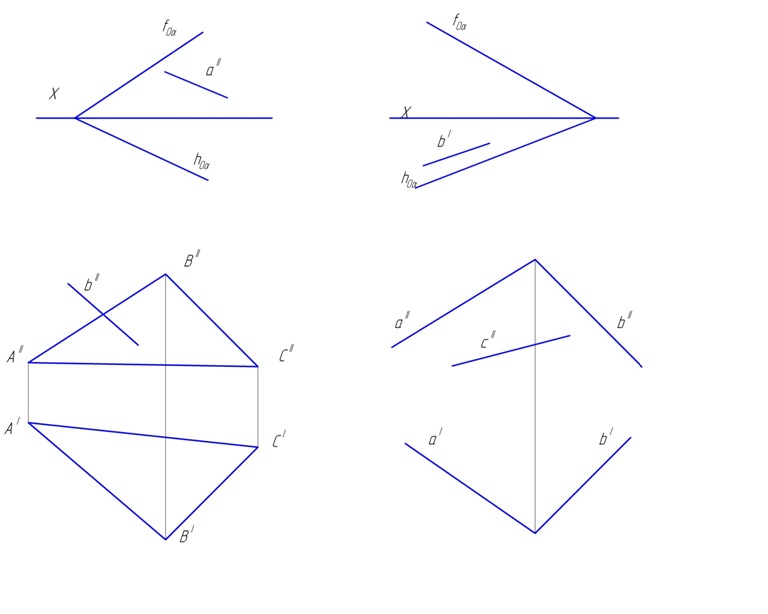
Рис. 57
2.3. Используя одну из главных линий плоскости построить недостающую проекцию точки, принадлежащей данной плоскости (рис. 58).
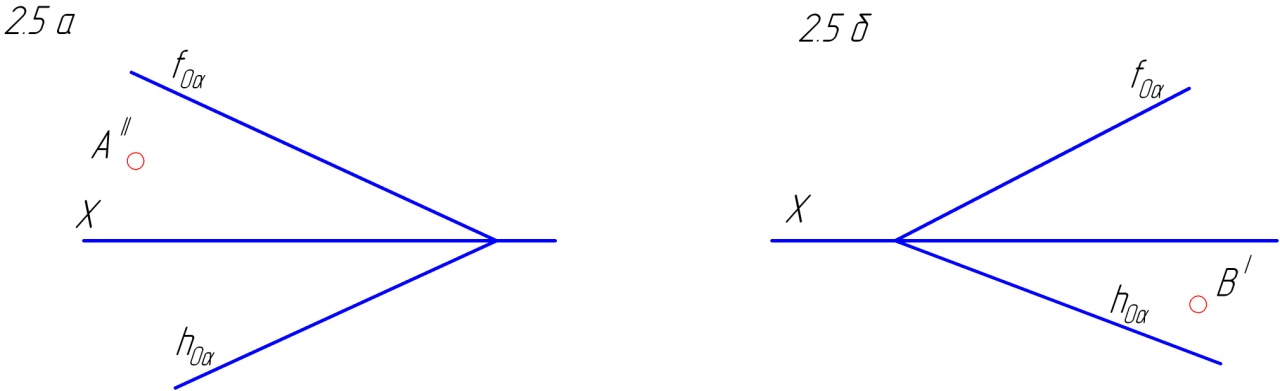
Рис. 58
2.4. Построить недостающие проекции точек, принадлежащих данным плоскостям (рис. 59).
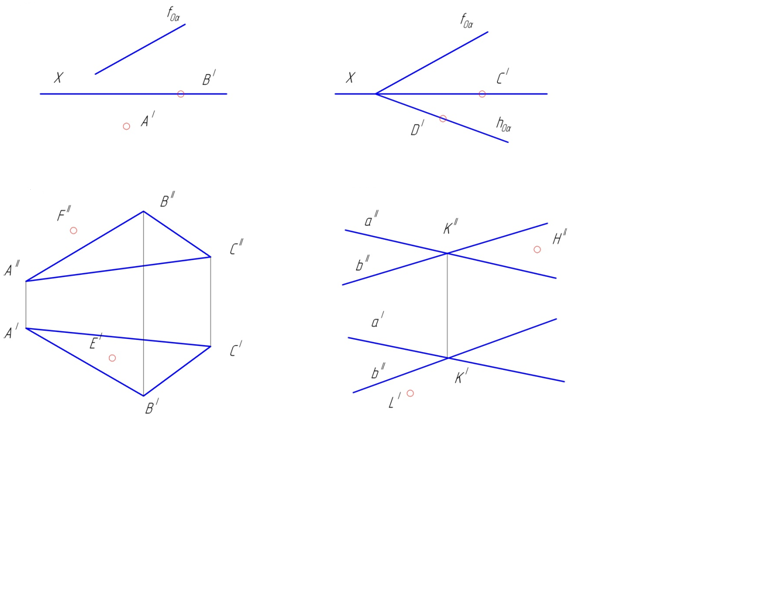
Рис. 59
2.5. Построить точку пересечения прямой с плоскостью, определить видимость прямой относительно заданной плоскости (рис. 60).
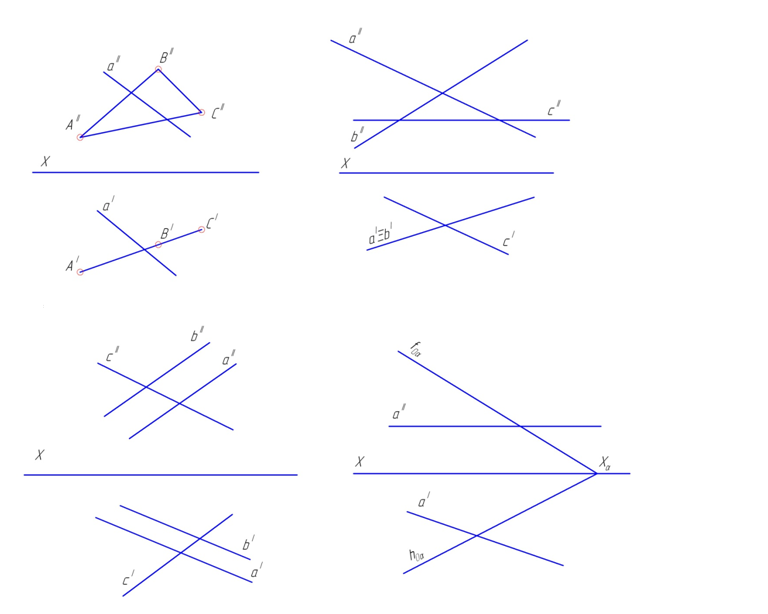
Рис. 60
2.6. Построить недостающие проекции точек (рис. 61), принадлежащих поверхностям, при условии что Е – видимая, N – невидимая на данной проекции.
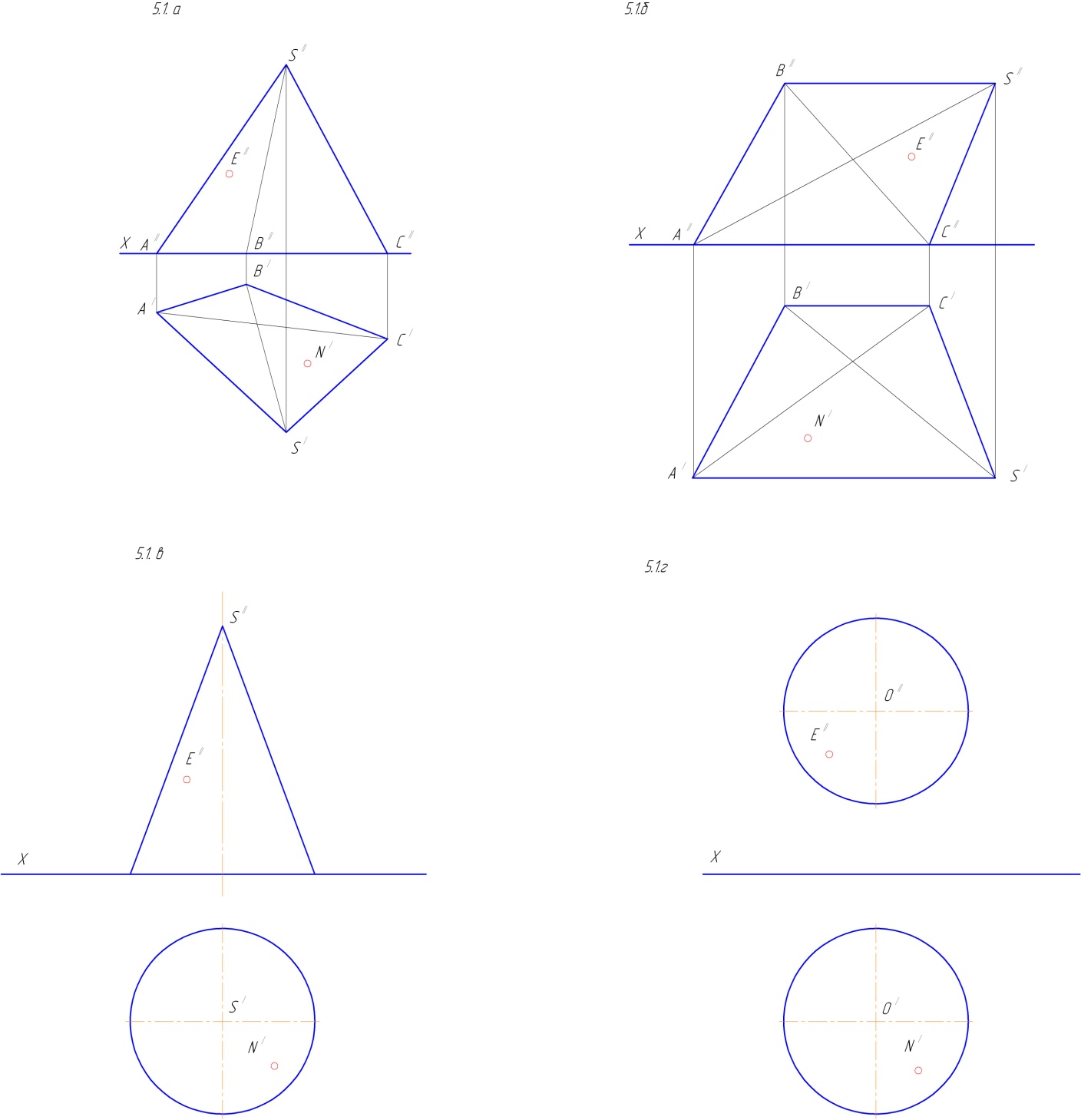

Рис. 61
Условия к задачам для самостоятельного решения по рисунку 62
1. По проекциям точки В, лежащей в плоскости α, заданной следами
hoα и ƒoα, построить профильный след Рoα..
2. Построить недостающие следы плоскостей α и β, заданных одним следом и точкой, лежащей в этой плоскости (А Э α; С Э β).
3. Через прямую m провести плоскость, заданную следами:
а) горизонтально-проецирующую;
б) фронтально-проецирующую.
4. Через точку А провести плоскость общего положения. Точка схода
следов βх задана.
5.Построить горизонтальную проекцию треугольника АВС, принадлежащего плоскости α.
6. Построить недостающие проекции точек E и F, лежащих в плоскости α.
7-13. Построить недостающие проекции фигуры, лежащей в плоскости.
14. Плоскость задана треугольником АВС. Построить следы этой плоскости.
15. Найти недостающие проекции трех точек (принадлежащих плоскости α) и построить проекции треугольника АВС, принадлежащего плоскости.
16. В плоскости α построить треугольник, одна сторона которого является горизонталью, вторая фронталью, третья профильной прямой.
17. По горизонтальному следу плоскости α и проекциям точки А, принадлежащей этой плоскости, построить её фронтальный след.
18. В плоскости β провести горизонталь на расстоянии 20 мм от π1.
19-21. Построить следы плоскости (hoα и ƒoα), заданной пересекающимися прямыми: прямой «l» и точкой схода следов αx.
22. Через точку В построить следы плоскости:
а) горизонтально-проецирующей,
б) фронтально-проецирующей.
23-24. Построить следы плоскости (hоα, ƒоα):
а) заданной параллельными прямыми;
б) проекциями трёх точек (А, В, С).
25-27. Построить недостающие проекции точек, принадлежащих заданным плоскостям.
28-30. В заданной плоскости построить горизонталь и фронталь.
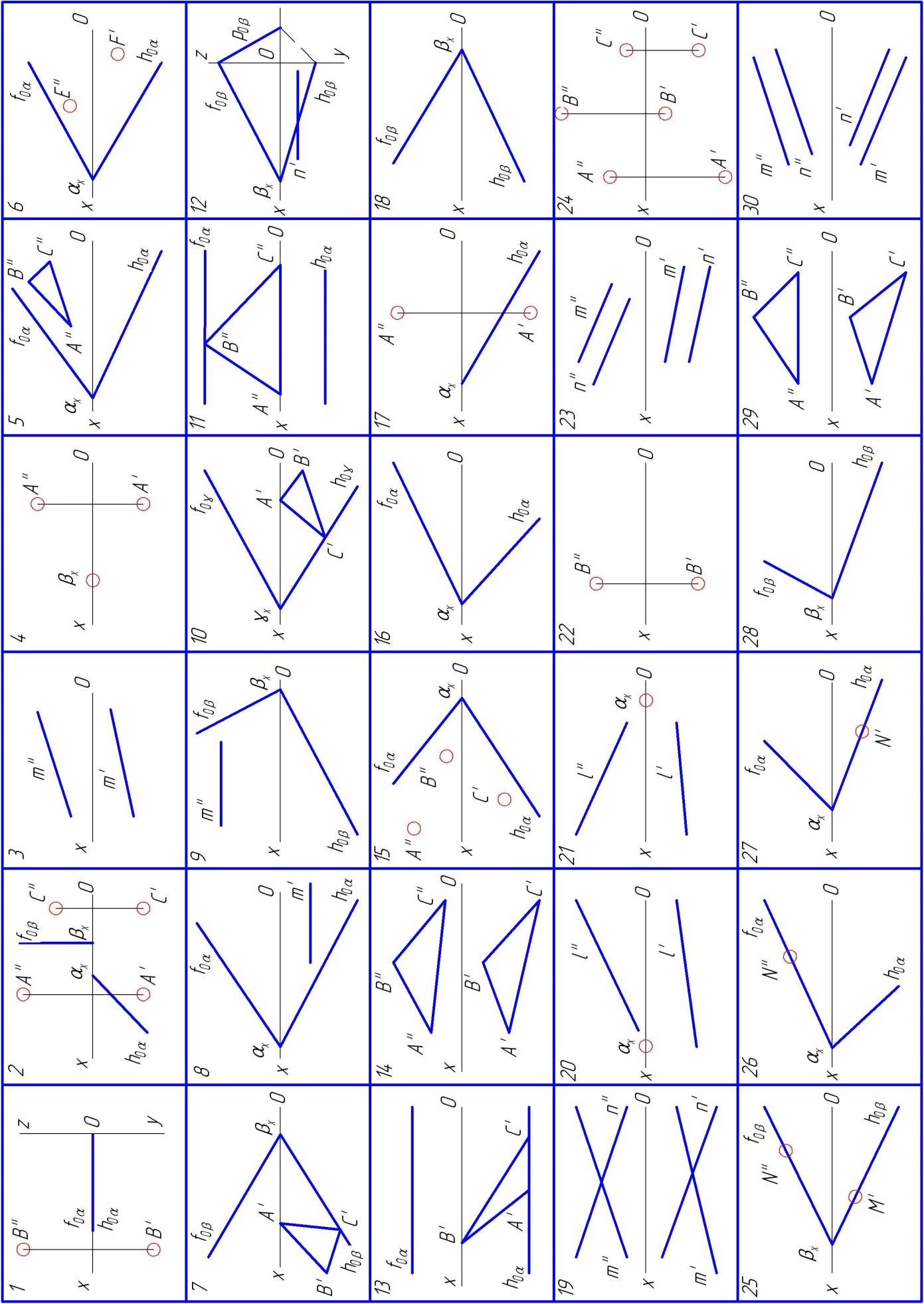 Рис. 62. Данные к задаче на тему плоскость
Рис. 62. Данные к задаче на тему плоскость
Контрольные вопросы
1. Как может быть задана плоскость на эпюре?
2. Что называется следом плоскости?
3. Какую плоскость называют плоскостью общего положения?
4. Какие плоскости относятся к плоскостям частного положения?
5. По каким признакам определяется принадлежность прямой к данной плоскости?
6. Какие линии, принадлежащие плоскости, называют главными?
7. Что называется многогранником, поверхностью вращения?
8. Каким способом определяется видимость ребер многогранника, по какому принцип?
9. Как находятся недостающие проекции точек, принадлежащих поверхности.
Лабораторная работа №3
