Методические указаня к задаче 12.
В задаче 12 необходимо построить контуры собственных и падающих теней заданного объекта (см. рис. 21). Исходные данные в виде чертежа в ортогональных проекциях в зависимости от варианта приведены на рис. 32 – 36; числовые значения исходных данных выбираются по табл. 2.
Приступая к решению задачи 12 необходимо изучить тему "Тени в ортогональных проекциях".
Построение теней восполняет основной недостаток ортогональных проекций - их малую наглядность.
В ортогональных проекциях обычно рассматривается солнечное освещение, при котором световые лучи параллельны друг другу. При этом за направление света 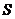 (рис.15, слева) принимают направление диагоналей куба, грани которого примыкают к плоскостям проекций. В этом случае горизонтальная
(рис.15, слева) принимают направление диагоналей куба, грани которого примыкают к плоскостям проекций. В этом случае горизонтальная 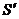 и фронтальная
и фронтальная  проекции световых лучей будут располагаться под углом 45° к оси проекций Х.
проекции световых лучей будут располагаться под углом 45° к оси проекций Х.
ТЕНЬ ОТ ТОЧКИ
Тень от точки есть точка пересечения светового луча, проходящего через эту точку, с плоскостью проекций или какой-либо поверхностью. Плоскости проекций считаются непрозрачными, поэтому действительной или реальной тенью считается тень, расположенная в первом октанте (тень  на рис.15); тени, расположенные в других октантах - мнимые (тень
на рис.15); тени, расположенные в других октантах - мнимые (тень 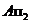 рис.15). Мнимые тени иногда используются при построении действительных теней.
рис.15). Мнимые тени иногда используются при построении действительных теней.
рис. 15
Нетрудно заметить, что построение тени от точки на произвольную заданную плоскость или поверхность сводится к определению точки пересечения светового луча, проведенного через заданную точку, с плоскостью или поверхностью. На рис.16 показано построение тени 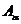 , отбрасываемой точкой
, отбрасываемой точкой 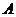 на горизонтально проецирующую плоскость
на горизонтально проецирующую плоскость 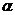 (слева) и плоскость общего положения, заданную четырехугольником
(слева) и плоскость общего положения, заданную четырехугольником 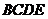 (справа).
(справа).
рис. 16
Здесь использован способ вспомогательных секущих плоскостей посредников, известный из метода ортогональных проекций. При этом через световой луч проведена вспомогательная горизонтально проецирующая плоскость посредник 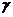 ; построена линия пересечения 1 – 2 вспомогательной плоскости
; построена линия пересечения 1 – 2 вспомогательной плоскости 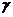 и заданных плоскостей; тень
и заданных плоскостей; тень 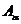 от точки
от точки 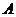 определена в пересечении линии 1 – 2 и светового луча.
определена в пересечении линии 1 – 2 и светового луча.
В случае построения теней вспомогательная плоскость 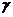 называется “лучевой плоскостью”, а линия 1 – 2 “лучевым сечением”. Сам метод построения тени, приведенный на рис. 16, называется методом лучевого сечения и является основным при построении теней.
называется “лучевой плоскостью”, а линия 1 – 2 “лучевым сечением”. Сам метод построения тени, приведенный на рис. 16, называется методом лучевого сечения и является основным при построении теней.
ТЕНЬ ОТ ПРЯМОЙ ЛИНИИ
Тень прямой линии на плоскость есть прямая линия, следовательно, для построения тени отрезка прямой на одну плоскость достаточно построить тени двух нетождественных точек, принадлежащих отрезку, и соединить их прямой (отрезок 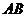 на рис.17). Тень от отрезка прямой, падающая на несколько плоскостей, есть ломаная линия с точками перелома на линии пересечения плоскостей (отрезок
на рис.17). Тень от отрезка прямой, падающая на несколько плоскостей, есть ломаная линия с точками перелома на линии пересечения плоскостей (отрезок 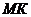 на рис.17). Для нахождения точки
на рис.17). Для нахождения точки 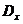 излома тени необходимо построить тень еще одной точки, принадлежащей отрезку. Это может быть или действительная тень
излома тени необходимо построить тень еще одной точки, принадлежащей отрезку. Это может быть или действительная тень 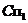 какой-либо третьей точки - точки
какой-либо третьей точки - точки 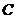 , или мнимая тень
, или мнимая тень 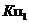 одного из концов отрезка - точки
одного из концов отрезка - точки 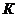 .
.
рис. 17
ТЕНИ ОТ ПРЯМЫХ ЧАСТНОГО ПОЛОЖЕНИЯ
В практике построения теней часто встречаются частные случаи взаимного расположения прямой и плоскости, на которую падает тень от прямой. В этих случаях при построении теней полезно пользоваться следующими правилами.
1. Тень от отрезка прямой, параллельной какой-либо плоскости, на которую падает от него тень, равна и параллельна самому отрезку.
Так на рис.18 прямая 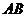 параллельна плоскости
параллельна плоскости 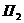 , поэтому тень от прямой на
, поэтому тень от прямой на 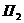 параллельна самой прямой
параллельна самой прямой 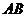 .
.
2. Тень от отрезка прямой перпендикулярной плоскости, на которую падает от него тень, совпадает с проекцией светового луча на эту плоскость.
На рис.18 отрезок 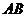 перпендикулярен
перпендикулярен 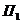 , поэтому тень
, поэтому тень 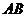 на
на 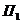 параллельна проекции
параллельна проекции 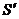 светового луча.
светового луча.
3. Тень от прямой, пересекающей плоскость, проходит через точку пересечения прямой и плоскости.
На рис.18 прямая пересекает плоскость 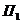 в точке
в точке 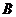 , следовательно, тень от
, следовательно, тень от 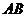 на
на 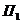 проходит через точку
проходит через точку 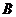 .
.
рис. 18
Правилами, приведенными выше, можно пользоваться также при построении теней в аксонометрических и перспективных проекциях.
Следующим правилом можно пользоваться только при построении теней в ортогональных проекциях; оно не действует при построении теней в аксонометрии и перспективе
4. Горизонтальная проекция тени от горизонтально проецирующей прямой, а так же фронтальная проекция тени от фронтально проецирующей прямой на любую поверхность, совпадают с горизонтальной и фронтальной проекциями светового луча соответственно.
МЕТОД ОБРАТНЫХ ЛУЧЕЙ
При построении теней, падающих от одного предмета на другой, применяют способ обратных лучей. В этом случае, прежде всего, строят тени заданных геометрических элементов на одну из плоскостей проекций и определяют точки пересечения теней. Через отмеченные точки проводят лучи, направление которых противоположно световым лучам (обратные лучи). Каждый из обратных лучей, пересекая данные геометрические элементы, определяет нужные для построения точки.
Применение этого метода показано на примере построения тени прямой 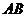 на плоскости треугольника
на плоскости треугольника 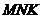 (рис. 19 вверху справа). Здесь построены падающие тени
(рис. 19 вверху справа). Здесь построены падающие тени 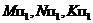 и
и 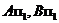 треугольника
треугольника 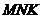 и прямой
и прямой 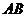 соответственно на плоскости
соответственно на плоскости 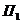 . Определены точки
. Определены точки 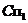 и
и 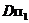 пересечения контуров падающих теней, из которых проведены обратные лучи, пересекающие заданные объекты в точках
пересечения контуров падающих теней, из которых проведены обратные лучи, пересекающие заданные объекты в точках 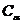 и
и 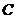 , а так же
, а так же 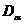 и
и 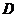 .
. 
Точки 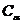 и
и 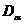 представляют собой тени от точек
представляют собой тени от точек 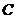 и
и 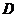 прямой
прямой 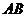 на стороны
на стороны 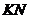 и
и 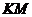 треугольника соответственно.
треугольника соответственно.
рис. 19
На рис. 19 внизу слева приведено решение задачи по построению тени 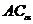 прямой
прямой 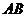 на плоскости треугольника KMN на эпюре. Тень прямой на плоскости треугольника пройдет через точку
на плоскости треугольника KMN на эпюре. Тень прямой на плоскости треугольника пройдет через точку 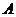 пересечения прямой с плоскостью треугольника (см. правило 3 на стр….) и точку
пересечения прямой с плоскостью треугольника (см. правило 3 на стр….) и точку 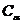 , которая построена методом обратного луча.
, которая построена методом обратного луча.
ТЕНИ СОБСТВЕННЫЕ И ПАДАЮЩИЕ
При рассмотрении теней геометрических тел основной задачей является определение контуров собственной и падающей теней, т.е. границы между освещенными и неосвещенными поверхностями. Собственная тень расположена на неосвещенных поверхностях самого предмета. Тени, отбрасываемые предметом на плоскости проекции и другие предметы называют падающими (рис.20). Между контурами падающей и собственной теней существует прямая зависимость: контур падающей тени есть тень от контура собственной тени. На рис.20 контур собственной тени - 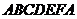 , контур падающей -
, контур падающей - 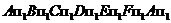 .
.
рис. 20
ПРИМЕР РЕШЕНИЯ КОНТРОЛЬНОГО ЗАДАНИЯ 12
На рис.21 приведен пример построения теней в ортогональных проекциях аналогичный задаче 12 контрольной работы №2. Объект состоит из двух призм: пятиугольной, боковые ребра которой параллельны плоскости 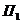 , и четырехугольной с боковыми ребрами перпендикулярными плоскости
, и четырехугольной с боковыми ребрами перпендикулярными плоскости 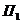 .
.
рис. 21
Лучи света направлены таким образом, чтобы тень от высокого объема падала на низкий. Определяем контуры собственных теней заданных объектов для каждого отдельно в предположении, что второй отсутствует. В даннои случае левые боковые, передние и верхние грани призм будут освещены а правые боковые и задние грани находятся в тени. Тогда контур собственной тени пятигранной призмы определит ломаная линия 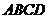 и далее заднее горизонтальное ребро призмы, проходящее через точку
и далее заднее горизонтальное ребро призмы, проходящее через точку 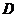 . Контур собственной тени четырехгранной призмы определит ломаная линия
. Контур собственной тени четырехгранной призмы определит ломаная линия 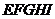 . По контурам собственных теней строим тени падающие. Тень от низкого объема падает только на плоскость проекции
. По контурам собственных теней строим тени падающие. Тень от низкого объема падает только на плоскость проекции 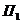 . Определяем тени от точек
. Определяем тени от точек 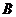 ,
, 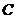 и
и 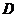 на плоскость
на плоскость 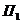 аналогично рис.15 и строим контур тени падающей от пятиугольной призмы. Тень от вертикального ребра
аналогично рис.15 и строим контур тени падающей от пятиугольной призмы. Тень от вертикального ребра 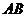 пройдет через точку
пройдет через точку 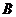 (правило 3 на стр. … ) и будет совпадать с горизонтальной проекцией светового луча (правило 2 на стр. … ). Затем контур падающей тени пройдет через точки
(правило 3 на стр. … ) и будет совпадать с горизонтальной проекцией светового луча (правило 2 на стр. … ). Затем контур падающей тени пройдет через точки 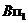 ,
, 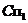 и
и 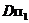 , и далее тень от горизонтального ребра, проходящего через точку
, и далее тень от горизонтального ребра, проходящего через точку 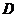 , будет параллельна самому ребру (правило 1 на стр. … ). После этого строим тень от контура четырехугольной призмы, которая падает на плоскость проекции
, будет параллельна самому ребру (правило 1 на стр. … ). После этого строим тень от контура четырехугольной призмы, которая падает на плоскость проекции 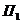 и пятиугольную призму. Тень от вертикального ребра
и пятиугольную призму. Тень от вертикального ребра 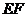 пройдет через точку
пройдет через точку  и будет совпадать с горизонтальной проекцией светового луча (правила 3 и 2 на стр. … ). В точке
и будет совпадать с горизонтальной проекцией светового луча (правила 3 и 2 на стр. … ). В точке 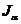 тень с плоскости
тень с плоскости 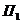 перейдет на вертикальную боковую грань пятиугольной призмы. Участок тени
перейдет на вертикальную боковую грань пятиугольной призмы. Участок тени 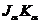 будет параллелен ребру
будет параллелен ребру 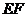 (правило 1 на стр. … ). На переднем, скате крыши тень от ребра
(правило 1 на стр. … ). На переднем, скате крыши тень от ребра 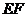 пройдет через точки
пройдет через точки 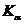 и 1 (правило 4 на стр. …), но закончится в точке
и 1 (правило 4 на стр. …), но закончится в точке 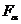 в которой световой луч, проведенный через точку
в которой световой луч, проведенный через точку 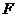 пересечется с контуром тени
пересечется с контуром тени 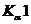 . Далее переходим к построению тени от ребра
. Далее переходим к построению тени от ребра 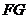 . На переднем скате крыши тень от ребра
. На переднем скате крыши тень от ребра 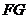 пройдет через точку
пройдет через точку 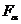 и точку 2, в которой ребро
и точку 2, в которой ребро 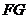 пересекается с передним скатом крыши, если последние продолжить (правило 3 на стр. … ). В точке
пересекается с передним скатом крыши, если последние продолжить (правило 3 на стр. … ). В точке 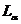 тень перейдет на задний скат крыши и далее пойдет в точку
тень перейдет на задний скат крыши и далее пойдет в точку 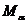 . Точка
. Точка 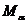 построена методом обратного луча (см. рис.19). Для этого определена точка
построена методом обратного луча (см. рис.19). Для этого определена точка 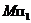 в пересечении теней от ребра
в пересечении теней от ребра 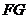 и горизонтального ребра пятиугольной призмы, проходящего через точку
и горизонтального ребра пятиугольной призмы, проходящего через точку 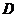 . Для построения тени от ребра
. Для построения тени от ребра 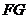 определены мнимая тень
определены мнимая тень 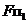 точки
точки 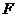 на
на 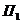 и действительная тень
и действительная тень 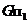 от точки
от точки 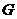 на
на 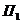 . Из точки
. Из точки 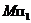 проведен обратный луч до пересечения с горизонтальным. ребром пятиугольной призмы, проходящим через точку
проведен обратный луч до пересечения с горизонтальным. ребром пятиугольной призмы, проходящим через точку 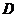 . Для построения точки
. Для построения точки 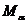 можно воспользоваться также правилом 3 (см. стр. … ). В точке
можно воспользоваться также правилом 3 (см. стр. … ). В точке 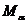 тень "соскользнет" с крыши и далее будет падать на плоскость
тень "соскользнет" с крыши и далее будет падать на плоскость 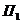 - точка
- точка 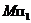 . Дальнейшие построение сводится к построению тени
. Дальнейшие построение сводится к построению тени 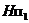 точки
точки 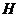 на плоскость
на плоскость 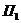 и соединению точек
и соединению точек 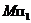 ,
, 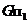 ,
, 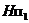 и
и 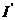 .
.
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ЗАДАНИЯ № 12
1. Оформить Формат A3 (изобразить рамку, основную надпись).
2. На формате в соответствии с вариантом, задания (рис. 32 – 36 и табл. 2) изобразить в масштабе 1:100 сначала горизонтальную и затем фронтальную проекции заданного объекта. Горизонтальную проекцию следует располагать от оси Х и правой рамки чертежа на расстояниях, указанных на рис.21. Положение угла 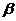 и направление световых лучей должно соответствовать таблице 3.
и направление световых лучей должно соответствовать таблице 3.
3. Определить и обозначить контуры собственной тени отдельно для каждого из зданий в предположении, что другое отсутствует.
4. По контуру собственной тени построить тень, падающую от низкого здания на плоскость 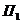 . Обозначить точки.
. Обозначить точки.
5. Используя контур собственной тени построить тень отбрасываемую высоким зданием на низкое и плоскость 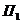 . Обозначить точки.
. Обозначить точки.
6. Обвести карандашом контуры здания и падающей тени сплошными основными толстыми линиями. Линии построения теней необходимо сохранить, обведя их сплошными тонкими линиями.
7. Сделать отмывку, штриховку или тушевку теней.
8. Оформить основную надпись.
