Прямая. Положение прямой относительно плоскостей проекций (прямые общего и частного положений). Определение натуральной величины отрезка прямой.Точка на прямой. Следы прямой

Положение прямой линии в пространстве определяется двумя точками или точкой и направлением.

Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

Прямая общего положения

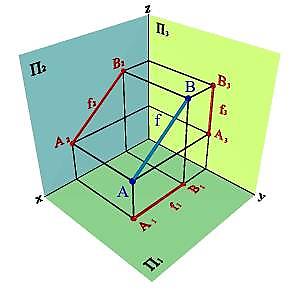
Прямая общегоположения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

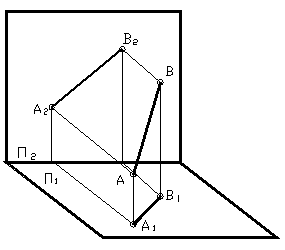
На эпюре проекции прямой общего положения составляют с осями проекций произвольные углы, поэтому величина каждой проекции меньше истинной величины самой прямой (рисунок 18).

Рисунок 18 – Изображение прямой общего положения

Прямые частного положения

Прямые, параллельные или перпендикулярные плоскостям проекций, называют прямыми частного положения.

Прямые частного положения делятся на прямые уровня и проецирующие прямые.

Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня:

1) прямую, параллельную горизонтальной плоскости проекций; называют горизонтальной или горизонтальюh (рисунок 19, 20);

2) прямую, параллельную фронтальной плоскости проекций; называют фронтальной или фронтальюf (рисунок 19, 20);

3)
прямую, параллельную профильной плоскости проекций; называют профильнойр (рисунок 19, 20).

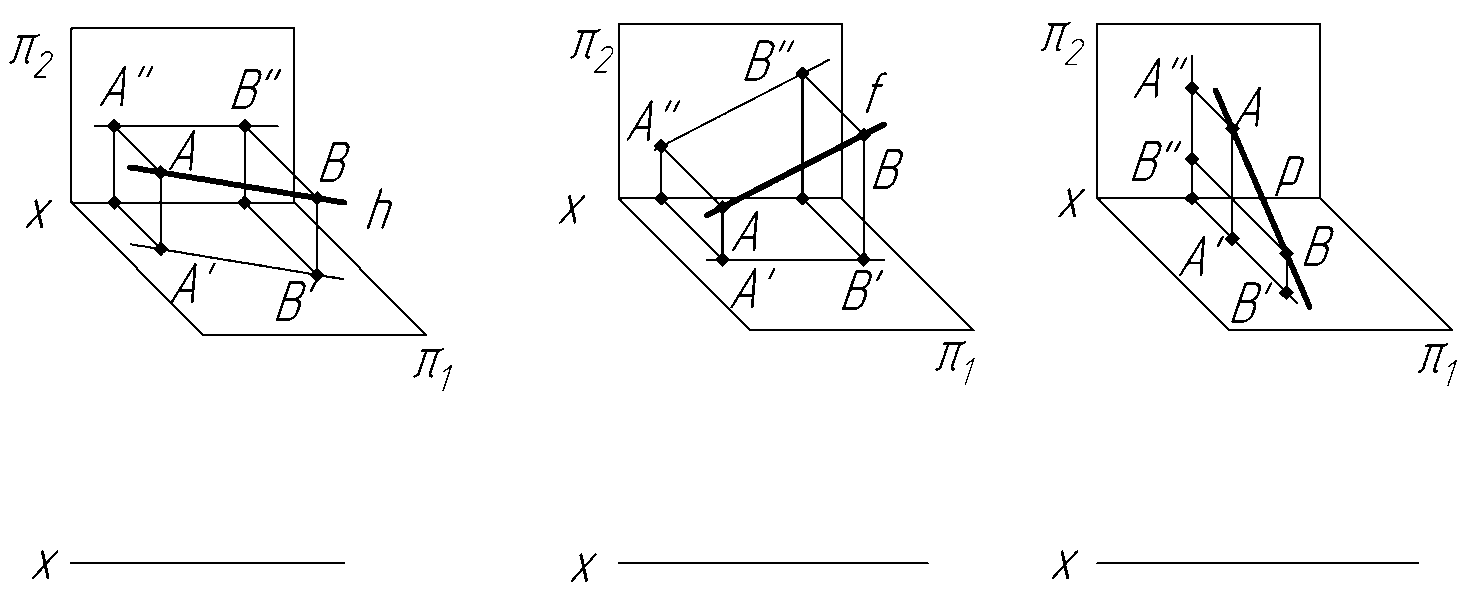
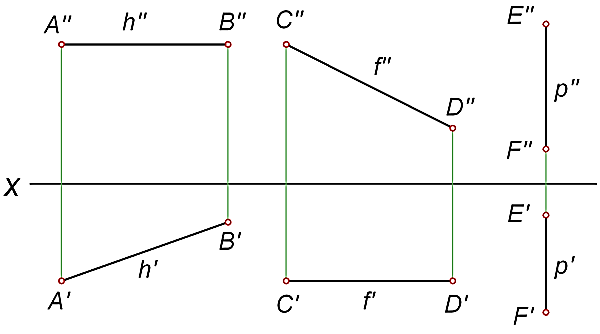
Рисунок 19 – Изображение линий уровня

Рисунок 20 – Изображение линий уровня

Каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона (α, β, γ), которые эта прямая образует с двумя другими плоскостями проекций, также будут проецироваться на эту плоскость без искажения.

Прямые уровня могут принадлежать плоскостям проекций. Такие прямые называют нулевой горизонталью и нулевой фронталью.

Прямые, перпендикулярные одной из плоскостей проекций, а двум другим параллельные, называются проецирующими:

1) горизонтально-проецирующая – прямая, перпендикулярная горизонтальной плоскости проекций (рисунок 21);

2) фронтально-проецирующая – прямая, перпендикулярная фронтальной плоскости проекций (рисунок 22);

3) профильно-проецирующая – прямая, перпендикулярная профильной плоскости проекций (рисунок 23).

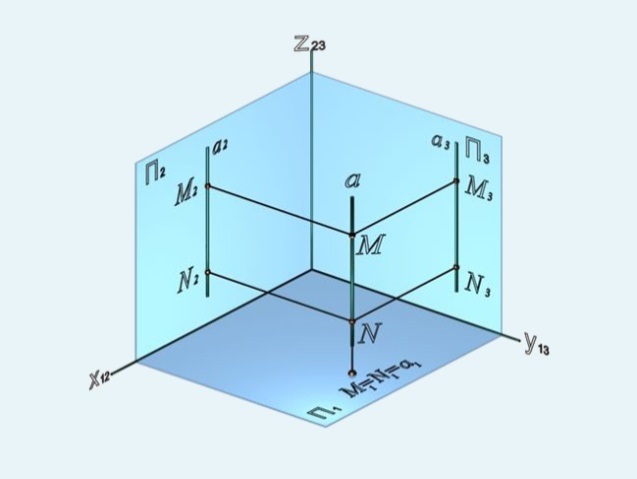
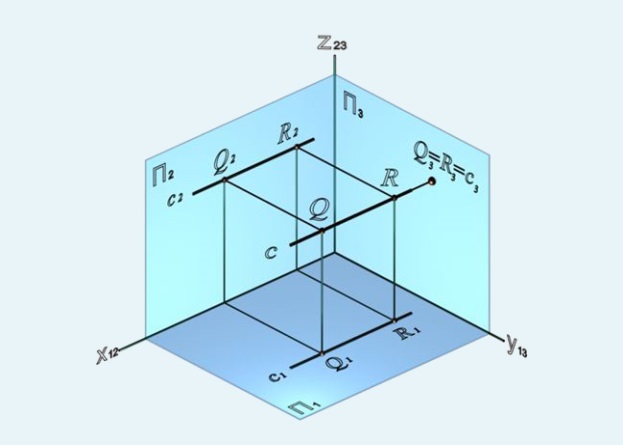
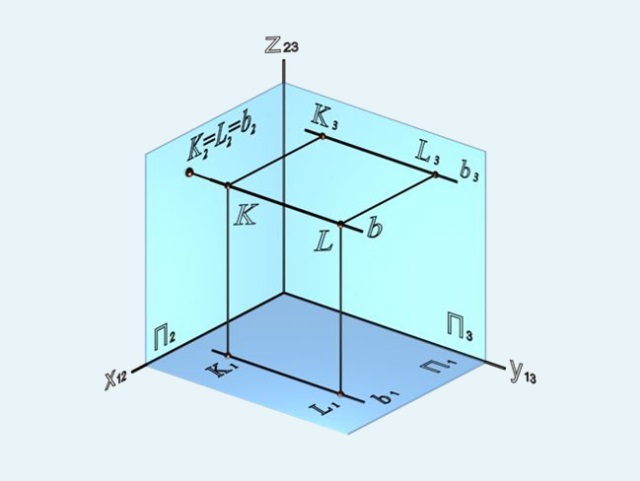
Рисунок 21 Рисунок 22 Рисунок 23

На рисунках 21-23 видно, что проекции прямых, перпендикулярных плоскостям проекций, на этих плоскостях представляют собой точки, а на тех плоскостях, которым прямые параллельны, проекции прямых будут перпендикулярны осям и равны по величине самим прямым.

Определение натуральной величины отрезка
иугла ее наклона прямой к плоскостям проекций

Таккакпрямаяобщегоположенияпроецируетсяна плоскости проекцийсискажением,тозадачаопределениянатуральной величины (НВ) прямой по её проекциям является важной. С целью определения НВ прямойразработанметодпрямоугольноготреугольника, сущность которого понятна из пространственного чертежа (рисунок 24а).

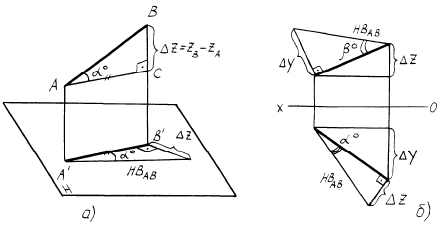
Длятого,чтобыопределитьнатуральнуювеличинупрямойпоеё проекциям,необходимонаоднойизеёпроекций (налюбой)построить прямоугольныйтреугольник,однимкатетомкоторогоявляетсясама проекция,адругимкатетом – разностьнедостающихкоординатконцов отрезка прямой. Тогда гипотенуза треугольника будет являться НВ прямой (рисунок 24б).

Рисунок 24 – Определение натуральной величины отрезка

Недостающей координатой здесь названа та координата, которая не участвует в построении той или иной проекции прямой. Так, например,горизонтальнаяпроекцияпрямойстроитсяпокоординатам X и Y её концов.Координата Z впостроенияхнеучаствуети называется недостающейкоординатой.Такимобразом,при построении прямоугольноготреугольниканагоризонтальнойпроекциипрямой на катете откладывают разность аппликат, а при построении на фронтальной проекции – разность ординат.

При определении НВ прямой методом прямоугольного треугольника одновременноможноопределитьуглынаклонапрямойк плоскостям проекций (углы αο и βο). Они определятся как углы между гипотенузой и соответствующей проекцией прямой.