Условные обозначения на чертеже

Часть I

Начертательная геометрия

Солигорск, 2017 г.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ…..…………………………………………………………….…..3

УСЛОВНЫЕ ОБОЗНАЧЕНИЕ НА ЧЕРТЕЖЕ.....………………..………….4

Тема 1.1 Введение в предмет начертательной геометриии образование проекционного чертежа………………………………………………………………5

Тема 1.2 Проекции отрезка прямой линии, положение прямой относительно плоскостей проекций, взаимное положение двух прямых, проецирование прямого угла………………………………………………………………………….14

Тема 1.3 Проекции плоскости, положение плоскости относительно плоскостей проекций, характерные линии плоскости…………………………………….22

Тема 1.4 Взаимное положение прямой и плоскости, двух плоскостей……31

Тема 1.5 Преобразование чертежа заменой плоскостей проекций, вращением и плоскопараллельным перемещением…………………………………………38

Тема 1.6 Поверхности – образование, изображение на чертеже,сечения плоскостями………………………………………………………………………….46

Тема 1.7 Пересечение поверхностей………………………………………...58

Тема 1.8 Развертки поверхностей……………………………………………66

Тема 1.9 Аксонометрическое проецирование………………………………73

ЗАКЛЮЧЕНИЕ……………………………………………………………….77

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ…………………………….78

ВВЕДЕНИЕ

Инженерная графика и инженерная и горная графика является первой инженерной дисциплиной, изучаемой студентами технических вузов.

Цель курса инженерной графики – дать студентам знания, умения и навыки, которые понадобятся инженеру любой специальности для изложения технических мыслей с помощью чертежа, а также для понимания по чертежу конструкций и принципа действия изображенного технического изделия.

Теоретическая часть курса инженерной графики базируется на положениях начертательной геометрии. Отдельные работы по проекционному черчению являются примерами практического применения методов начертательной геометрии.

В процессе изучения курса инженерной графики студенты получают представление о деталях, сборочных единицах и их чертежах, а также знакомят с элементами конструирования деталей и элементами технологии их обработки.

Инженерная графи3ка – первая ступень, на которой изучаются основные правила выполнения и оформления конструкторской документации.

Приобретение устойчивых навыков в выполнении чертежей достигается в результате усвоения всего комплекса технических дисциплин соответствующего профиля, подкрепленного практикой курсового и дипломного проектирования.

УСЛОВНЫЕ ОБОЗНАЧЕНИЯ НА ЧЕРТЕЖЕ

1. Точки, расположенные в пространстве, обозначаются прописными буквами латинского алфавита: A, B, C, D, …,L, N…

2. Линии общего положения обозначаются строчными буквами латинского алфавита: a, b, c, d, … l, n…

3. Линии уровня обозначаются: h – горизонталь,f – фронталь.

4. Поверхности обозначаются прописными буквами греческого алфавита A, B, Г, …, Р, Т…

5. Углы обозначаются строчными буквами греческого алфавита: α, β, γ, δ, φ…

6. Плоскости проекций обозначаются:

П₁– горизонтальная плоскость проекций;

П₂– фронтальная плоскость проекций;

П₃– профильная плоскость проекций.

7. Проекции точек, линий, поверхностей обозначаются теми же буквами, что и оригинал, с добавлением индекса плоскости проекций:

A₁, B₁…, a₁, b₁… – горизонтальные проекции;

A₂, B₂…, a₂, b₂… – фронтальные проекции;

A₃, B₃…, a₃, b₃… – профильные проекции.

Тема 1.1 Введение в предмет начертательной геометрии
и образование проекционного чертежа

Метод проецирования. Центральное и параллельное проецирование. Основные свойства.Прямоугольное (ортогональное) проецирование

Для отображения геометрической фигуры на чертеже применяют операцию проецирования. Она заключается в том, чточерезточку пространствапроводятпроецирующуюпрямуюдопересеченияс плоскостьюпроекций.Точкупересеченияпроецирующейпрямойс плоскостьюпроекцийназываютпроекциейданнойточкинаданную плоскость проекций.

Различаютследующиеметодыпроецирования:центральное, параллельное (косоугольноеиортогональное),перспективное, аксонометрическое и др.

Центральноеиперспективноепроецированиенашлоширокое применениевархитектуреистроительстве,ортогональное (прямоугольное) и аксонометрическое – в машино- и приборостроении.

Чертежи,построенныепометодупроецирования,называются проекционными.

Центральное проецирование

Пусть в пространстве задана плоскость α, которую будем называть плоскостью проекций.

Выберем какую-либо точку S, не лежащую на плоскости проекций. Эту точку будем называть центром проецирования.

Заданные точки А, В, С пространства будем проецировать на плоскость проекций α. Для этого через точки А, В, С из центра проекций S проведем прямые. Эти прямые будет называться проецирующей прямой. Затем находим точку пересечения А_1, В₁,С₁проецирующей прямой SA,SB, SC с плоскостью проекций α. Точка А_1, В₁,С₁ будет называться проекцией точек А, В, С (рисунок 1).

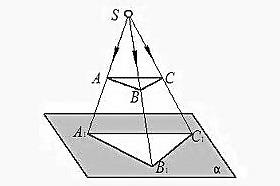
Рисунок 1 – Центральное проецирование

Очевидно, что каждой точке пространства будет однозначно соответствовать своя собственная проекция. Однако на рисунке 2 мы видим, что проекцией точки А и точки В является точка пересечения их общей проецирующей прямой с плоскостью проекций.

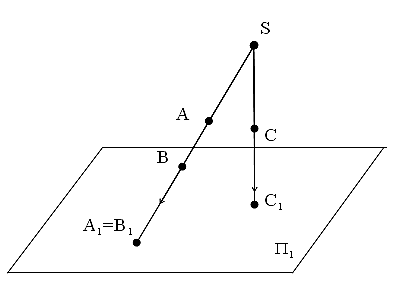
Рисунок 2 – Центральное проецирование

Следовательно, такое изображение не является взаимно однозначным, и судить о положении точек А и Вв пространстве по одной проекции нельзя, потому что одним из требований, предъявляемых к чертежам, является точное определение положения пространственного объекта по его изображению, по его проекциям.

Параллельное проецирование

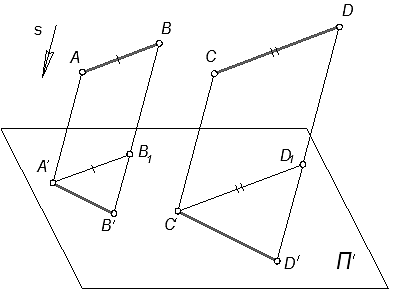
Если центр проецирования S_∞ удален в бесконечность (рисунок 3), то проецирующие лучи станут параллельны друг другу. Такое проецирование называется параллельным.

Рисунок 3 – Параллельное проецирование

Проецирующие лучи, исходящие из бесконечного далека, могут быть наклонены под любым углом к плоскости проекций.

При заданном аппарате проецирования можно построить параллельную проекцию любой точки пространства. Для этого через заданные точки А и В проведем проецирующие прямые, параллельную направлению s, и найдем точки А_1, В₁ – точки пересечения этой прямой с плоскостью проекций П₁.

Через точки А и В параллельно заданному направлению в пространстве можно провести только одну прямую, следовательно, каждая точка пространства имеет одну и только одну параллельную проекцию.

Точки А и В принадлежат одному и тому же проецирующему лучу, параллельному направлению s. Поэтому проекции этих точек В₁ и А₁ совпадают. Отсюда следует, что по одной заданной проекции положение в пространстве точек В и А определить невозможно.

Прямая общего положения

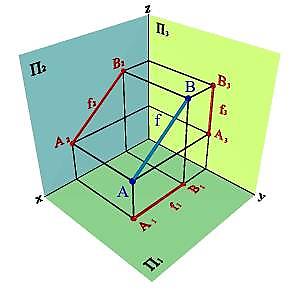
Прямая общегоположения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

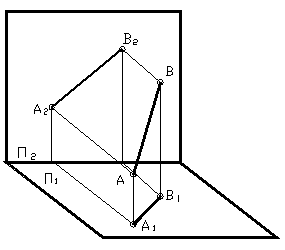
На эпюре проекции прямой общего положения составляют с осями проекций произвольные углы, поэтому величина каждой проекции меньше истинной величины самой прямой (рисунок 18).

Рисунок 18 – Изображение прямой общего положения

Прямые частного положения

Прямые, параллельные или перпендикулярные плоскостям проекций, называют прямыми частного положения.

Прямые частного положения делятся на прямые уровня и проецирующие прямые.

Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня:

1) прямую, параллельную горизонтальной плоскости проекций; называют горизонтальной или горизонтальюh (рисунок 19, 20);

2) прямую, параллельную фронтальной плоскости проекций; называют фронтальной или фронтальюf (рисунок 19, 20);

3)
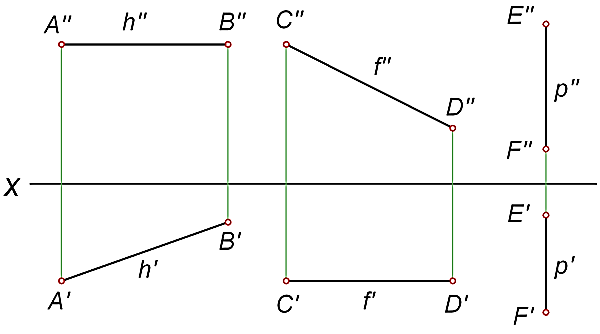
прямую, параллельную профильной плоскости проекций; называют профильнойр (рисунок 19, 20).

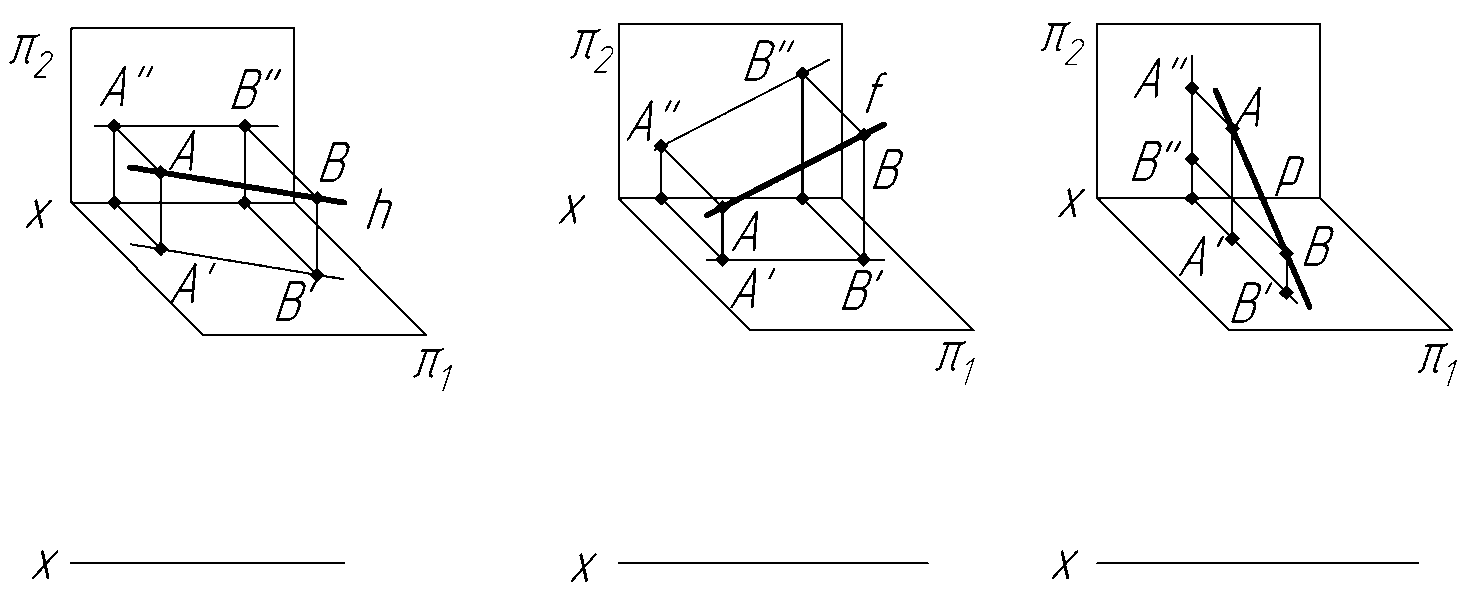
Рисунок 19 – Изображение линий уровня

Рисунок 20 – Изображение линий уровня

Каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона (α, β, γ), которые эта прямая образует с двумя другими плоскостями проекций, также будут проецироваться на эту плоскость без искажения.

Прямые уровня могут принадлежать плоскостям проекций. Такие прямые называют нулевой горизонталью и нулевой фронталью.

Прямые, перпендикулярные одной из плоскостей проекций, а двум другим параллельные, называются проецирующими:

1) горизонтально-проецирующая – прямая, перпендикулярная горизонтальной плоскости проекций (рисунок 21);

2) фронтально-проецирующая – прямая, перпендикулярная фронтальной плоскости проекций (рисунок 22);

3) профильно-проецирующая – прямая, перпендикулярная профильной плоскости проекций (рисунок 23).

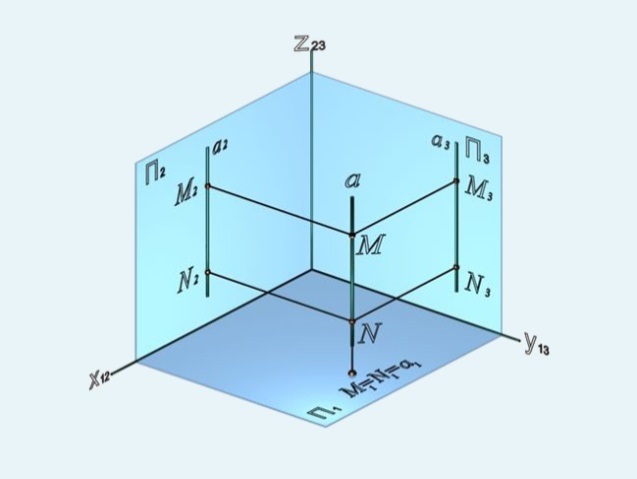
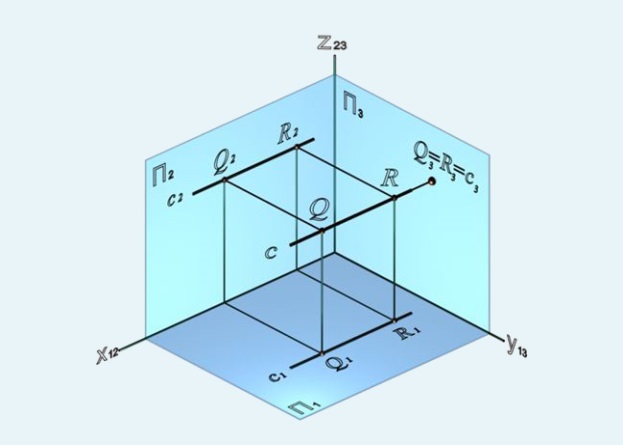
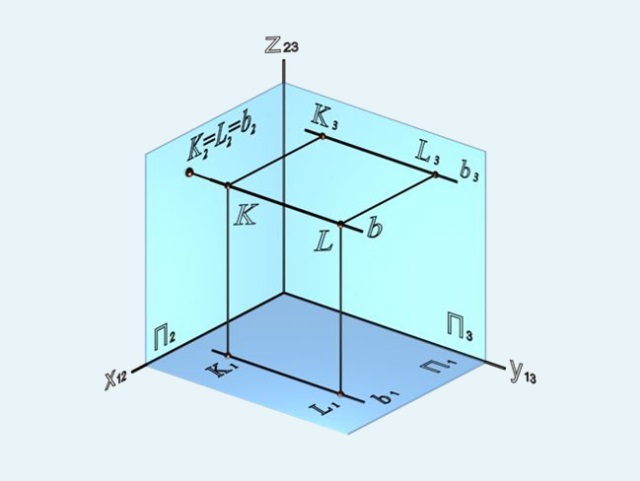
Рисунок 21 Рисунок 22 Рисунок 23

На рисунках 21-23 видно, что проекции прямых, перпендикулярных плоскостям проекций, на этих плоскостях представляют собой точки, а на тех плоскостях, которым прямые параллельны, проекции прямых будут перпендикулярны осям и равны по величине самим прямым.

Определение натуральной величины отрезка
иугла ее наклона прямой к плоскостям проекций

Таккакпрямаяобщегоположенияпроецируетсяна плоскости проекцийсискажением,тозадачаопределениянатуральной величины (НВ) прямой по её проекциям является важной. С целью определения НВ прямойразработанметодпрямоугольноготреугольника, сущность которого понятна из пространственного чертежа (рисунок 24а).

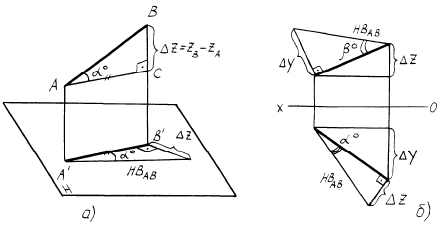
Длятого,чтобыопределитьнатуральнуювеличинупрямойпоеё проекциям,необходимонаоднойизеёпроекций (налюбой)построить прямоугольныйтреугольник,однимкатетомкоторогоявляетсясама проекция,адругимкатетом – разностьнедостающихкоординатконцов отрезка прямой. Тогда гипотенуза треугольника будет являться НВ прямой (рисунок 24б).

Рисунок 24 – Определение натуральной величины отрезка

Недостающей координатой здесь названа та координата, которая не участвует в построении той или иной проекции прямой. Так, например,горизонтальнаяпроекцияпрямойстроитсяпокоординатам X и Y её концов.Координата Z впостроенияхнеучаствуети называется недостающейкоординатой.Такимобразом,при построении прямоугольноготреугольниканагоризонтальнойпроекциипрямой на катете откладывают разность аппликат, а при построении на фронтальной проекции – разность ординат.

При определении НВ прямой методом прямоугольного треугольника одновременноможноопределитьуглынаклонапрямойк плоскостям проекций (углы αο и βο). Они определятся как углы между гипотенузой и соответствующей проекцией прямой.

Взаимное положение прямых

(параллельные, пресекающиеся, скрещивающиеся).

Конкурирующие точки

Прямые в пространстве могут занимать различное взаимное положение. Они могут быть параллельными, пересекающимися и скрещивающимися (рисунок 28).

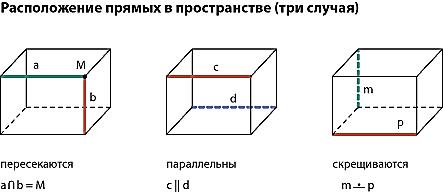
Рисунок 28 – Расположение прямых в пространстве (три случая)

Если прямые в пространстве пересекаются, то на эпюре их одноименные проекции пересекаются, и точки пересечения проекций этих прямых лежат на одной линии связи (рисунок 29).

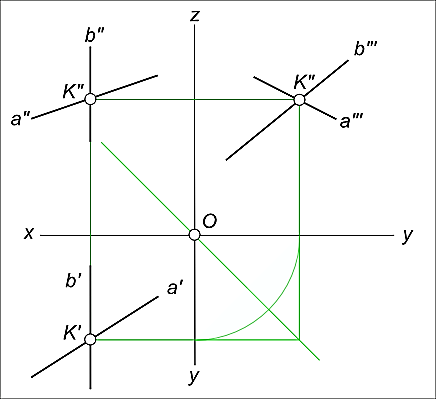
Рисунок 29 – Пересекающиеся прямые

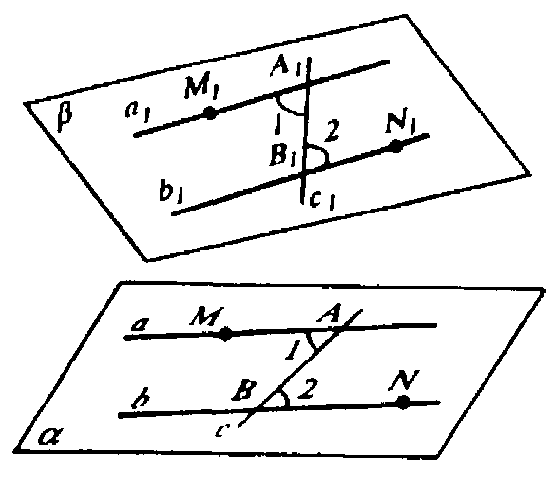
Если прямые в пространстве параллельны, то на эпюре их одноименные проекции параллельны. На рисунке 30 изображены прямые общего положения а и b, их горизонтальные и фронтальные проекции параллельны между собой. Можно утверждать, что и в пространстве эти прямые параллельны.

Рисунок 30 – Параллельные прямые

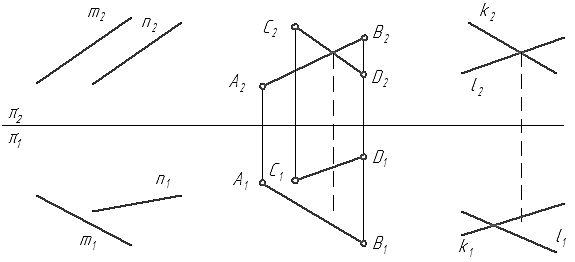
Если прямые в пространстве не пересекаются и не параллельны между собой, то такие прямые называются скрещивающимися. На эпюре точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи.

Рисунок 31 – Скрещивающиеся прямые

Эти точки не являются общими для прямых (рисунок 31). Точка пересечения одноименных проекций скрещивающихся прямых является на эпюре проекцией двух конкурирующих точек, принадлежащих заданным прямым.

Конкурирующие точки

Конкурирующие точки используются для определения видимости геометрических фигур на плоскости проекций. Где видимые объекты отображают сплошной основной линией, не видимые – тонкой пунктирной линией.

Конкурирующие точки–это точки, лежащие на одном перпендикуляр к плоскости проекций.

На рисунке 32а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П₁ [А₁ = В₁]. Такие точки называются горизонтально конкурирующими.

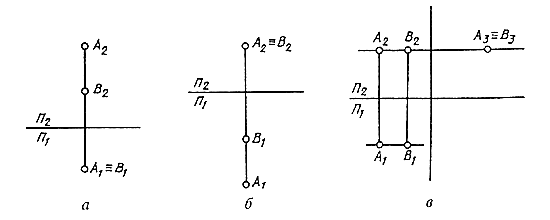
Если проекции точек A и В совпадают на плоскости П₂ (рисунок 32б), они называются фронтально конкурирующими. И если проекции точек А и Всовпадают на плоскости П₃[А₃ = B₃] (рисунок 32в), они называются профильно конкурирующими.

Рисунок 32 – Определение конкурирующих точек

По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих – та, у которой больше глубина, и у профильно конкурирующих – та, у которой больше широта.

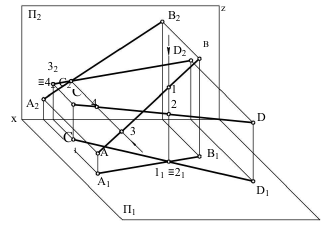
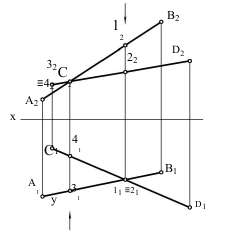
На эпюре (рисунок 33) горизонтальные проекции конкурирующих точек 1₁ и 2₁ совпадают, но точка 1 принадлежит прямой АВ, а точка 2 – прямой СD.

Рисунок 33 – Определение конкурирующих точек

Изчертежавидно,чторасстоянияотплоскостиП₁доточек1и2 различны. Фронтальная проекция перпендикуляра, обозначенная стрелкой, позволяет определить, какая из точек расположена ниже. В данном примере точка 2, лежащая на прямой CD, расположена ниже, чем точка 1, лежащая на прямой АВ. Следовательно, прямая CD проходит под прямой АВ.

Точке пересечения фронтальных проекций соответствуют точки 3 и 4, расположенные на прямых АВ и CD. Горизонтальная проекция перпендикуляра, отмеченная стрелкой, позволяет определить, какая из этих точек ближе к наблюдателю. Из чертежа видно, что точка 3 расположена ближе к наблюдателю, чем точка 4. Поэтому прямая АВ проходит перед CD.

Тема 1.3 Проекции плоскости, положение плоскости относительно
плоскостей проекций, характерные линии плоскости

1.3.1 Задание плоскости на чертеже различными способами.
Следы плоскости. Характерные прямые плоскости
– линии уровня и линии наибольшего наклона плоскости

Задание плоскости на чертеже различными способами

Что такое плоскость? Из геометрии известно, что плоскость представляет собой бесконечную поверхность, которая на всем своем протяжении имеет одинаковое направление. Примером получения плоскости в пространстве может служить параллельное перемещение одной прямой по второй неподвижной прямой. Простейшими плоскостями считаются плоские геометрические фигуры (треугольник, круг и т.п.)

Плоскость на чертеже может быть задана (рисунок 34):

– проекциями трех точек, не лежащих на одной прямой (рисунок 34, 1);

– проекциями отрезка прямой и точкой, не лежащей на прямой (рисунок 34, 2);

– проекциями двух пересекающихся отрезков прямых (рисунок 34, 3);

– проекциями двух отрезков параллельных прямых (рисунок 34, 4);

– проекциями плоской фигуры (треугольника) (рисунок 34, 5);

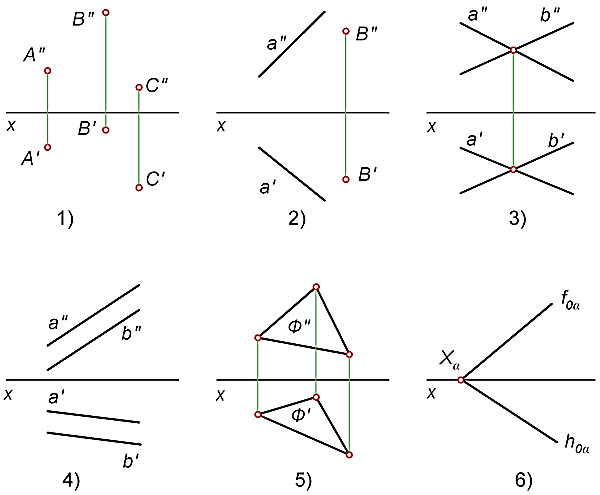
– следами (рисунок 34, 6).

Рисунок 34 – Способы задания плоскости на чертеже

Соединяя проекции точек на первых четырех рисунках, можно перейти к изображению в виде треугольника или других плоских фигур.

Следы плоскости

Плоскость Ʃ (рисунок 35,а) образует с плоскостями проекций П₂ и П₁ трехгранный угол, вершина которого находится в пересечении следов. Две грани этого угла совпадают с плоскостями проекций и находятся между осью х и следами плоскости (Ʃ₁ и Ʃ₂), а третий угол – между следами Ʃ₁ и Ʃ₂, – всегда меньше суммы двух других углов. Это значит, что на чертеже угол, заключенный между следами Ʃ₁ и Ʃ₂(рисунок 35, б), всегда больше угла, заключенного между этими следами в пространстве (рисунок 35, а).

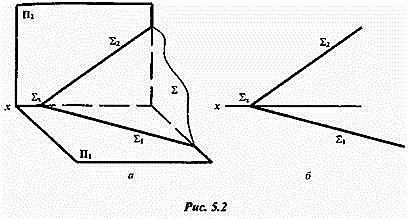
Рисунок 35 – Определение следа прямой

На рисунке 35 показаны горизонтальный Ʃ₁и фронтальный Ʃ₂ следы. Точка пересечения следов, расположенная на оси х, называется точкой схода следов (Ʃ_х). Так как след плоскости является прямой, лежащей в плоскости проекций, то горизонтальная проекция фронтального следа Ʃ₂ будет находиться на оси х. Здесь же будет находиться и фронтальная проекция Ʃ₁ горизонтального следа плоскости Ʃ. Обычно эти проекции следов не используются при решении задач и поэтому их можно не изображать и не обозначать.

Целесообразно следы плоскости обозначить на чертежах по наименованию самих плоскостей проекций (П₁, П₂) или по обозначению их индексов, например, Ʃ_п1 и Ʃ_п2, или же Ʃ₁ и Ʃ₂ (рисунок 35). Такое обозначение более удобно при решении задач. Следует иметь в виду, что со следами плоскости совпадают (сливаются) их проекции. Так, с горизонтальным следом плоскости П₁ совпадает горизонтальная проекция этого следа, а с фронтальным следом плоскости П₂ совпадает фронтальная проекция этого следа.

Характерные прямые плоскости – линии уровня
и линии наибольшего наклона плоскости

К главным линиям (характерным прямым) плоскости относятся линии уровня и линии наибольшего наклона (рисунок 36).

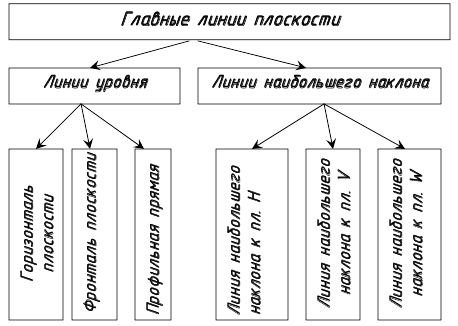
Рисунок 36 – Классификация главных линий плоскости

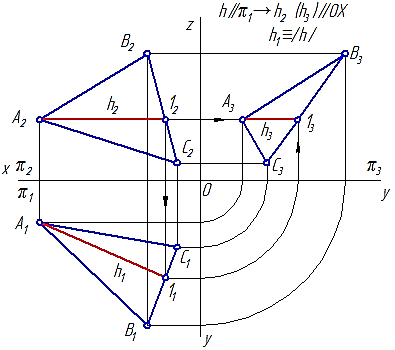
Горизонталью h (h₁ и h₂) плоскости называется прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (рисунок 37). Так как горизонталь плоскости параллельна горизонтальной плоскости проекций П₁, то фронтальная ее проекция будет параллельна оси Х. Для построения проекций горизонтали проводим через точку А₂ прямую, параллельную оси Х. Это будет фронтальная проекция горизонтали (h₂). Горизонтальную проекцию горизонтали (h₁) находим по линии связи.

Рисунок 37 – Горизонталь плоскости

Фронталью плоскости f (f₁ и f₂) называется прямая, лежащая в данной плоскости и параллельная фронтальной плоскости проекций. Горизонтальная проекция фронтали на чертеже параллельна оси Х, а фронтальную проекцию фронтали находим при помощи линии связи (рисунок 38).

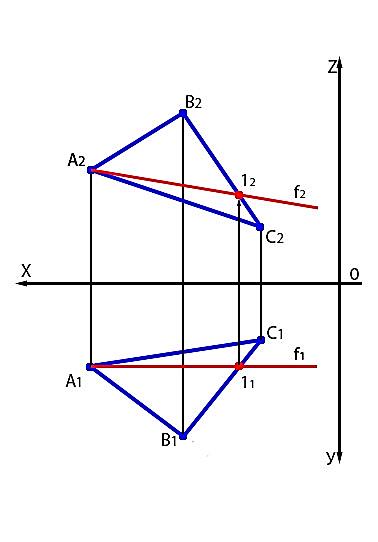
Рисунок 38 – Фронталь плоскости

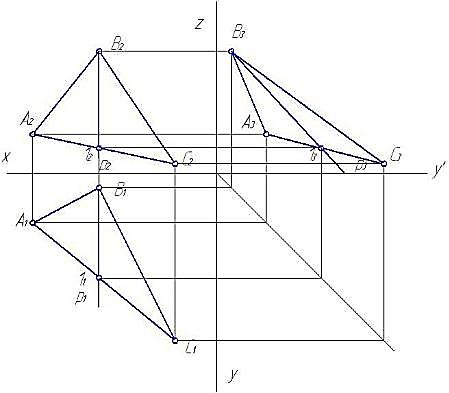
Профильной прямойр (р₁, р₂, р₃) называется прямая линия, принадлежащая плоскости и параллельная профильной плоскости проекций (рисунок 39).

Рисунок 39 – Профильная прямая

В этом случае фронтальная и горизонтальная проекции профильной прямой р (р₁ и р₂) параллельны П₃, а профильная проекция р₃равняется натуральной величиной.

Линиями наибольшего наклона плоскости к плоскостям проекций (ЛНН) называютсялинии,проведенныевплоскостииопределяющие наибольший угол между плоскостью и плоскостью проекций, т.е. величину образованного двугранного угла. Различают линию наибольшего наклона плоскости к плоскости проекций H (горизонтальная плоскость) – ЛНН(Н), к плоскости проекций V (фронтальная плоскость) – ЛНН(V) и кплоскости проекций W (профильная плоскость) – ЛНН(W).Рассмотримподробнее первые две линии.

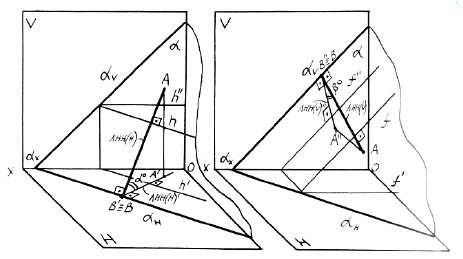
ЛиниянаибольшегонаклонаплоскостикплоскостипроекцийH проводитсяперпендикулярнокгоризонтальномуследуплоскостиилик горизонталиплоскости.Линиянаибольшегонаклонаплоскостик плоскостипроекцийVпроводитсяперпендикулярнокфронтальному следу плоскости или к фронтали (рисунок 40).

Рисунок 40 – Построение проекций линий наибольшего наклона

ПринципметодикипостроенияпроекцийЛННосновываетсяна теореме прямого угла: если один из катетов прямого углапараллеленкакой-либоплоскости,тонаэтуплоскостьпрямойугол проецируется в натуральную величину.

1.3.2 Положение плоскости относительно плоскостей проекций
(плоскости общего и частного положения).
Точка и прямая в плоскости (построение их недостающих проекций)

Положение плоскости относительно плоскостей проекций
(плоскости общего и частного положений)

Плоскость в пространстве может занимать относительно плоскостей проекций П₁, П₂, П₃ следующие положения:

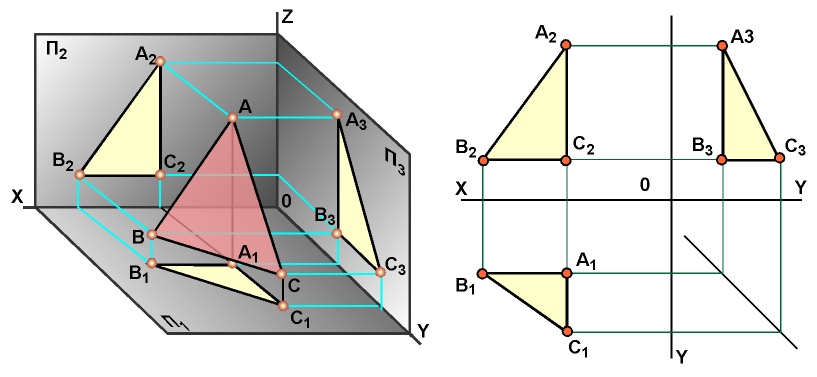
– наклонно ко всем плоскостям проекций – плоскость общего положения (рисунок 41);

Рисунок 41 – Плоскость общего положения

– перпендикулярно к одной из плоскостей проекций – проецирующая плоскость;

– перпендикулярно одновременно к двум плоскостям проекций, т.е. параллельно третьей плоскости проекций – плоскость уровня.

Проецирующие плоскости: горизонтально-проецирующая, фронтально-проецирующая, профильно-проецирующая.

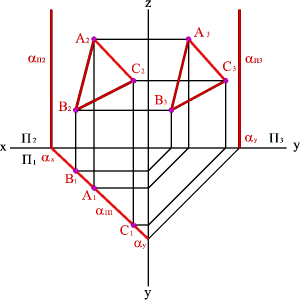
Плоскость перпендикулярная горизонтальной плоскости проекций, называется горизонтально проецирующей плоскостью.Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскостисовпадают с горизонтальным следом (рисунок 42).

Рисунок 42 – Горизонтально проецирующая плоскость

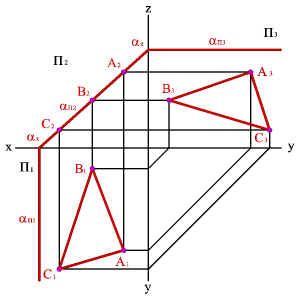
Плоскость перпендикулярная фронтальной плоскости проекций – фронтально-проецирующая плоскость. Фронтальной проекцией плоскости является прямая линия, совпадающая с фронтальным следом следом (рисунок 43).

Рисунок 43 – Фронтально проецирующая плоскость

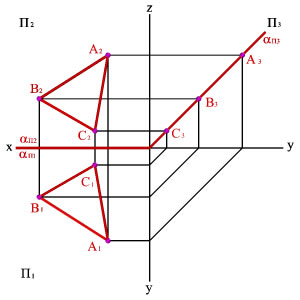
Профильно-проецирующая плоскость– плоскость, перпендикулярная профильной плоскости проекций, задается профильным следом плоскости (рисунок 44).

Рисунок 44 – Профильно-проецирующая плоскость

Плоскости уровня: горизонтальная плоскость – параллельная П₁, фронтальная – параллельная П₂ и профильная – параллельная П₃. Эти плоскости уровня перпендикулярны одновременно двум другим плоскостям проекций.

Горизонтальная плоскость уровня– плоскость, параллельная горизонтальной плоскости проекций и перпендикулярна одновременно фронтальной и профильной плоскостям проекций.

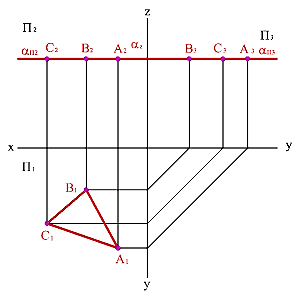
Горизонтальная плоскость, заданная треугольником АВС (рисунок 45), изображена проекциями А₁В₁С₁, А₂В₂С₂ и А₃В₃С₃. При этом фронтальная и профильная проекции изображаются отрезками прямых линий, а горизонтальная – треугольником, который равняется истинной величине треугольника АВС, т.к. он в пространстве занимает параллельное положение относительно плоскости проекций П₁.

Рисунок 45 – Горизонтальная плоскость уровня

Фронтальная плоскость уровня– плоскость, параллельная фронтальной плоскости проекций и перпендикулярна одновременно горизонтальной и профильной плоскостям проекций.

Фронтальная плоскость, заданная треугольником АВС (рисунок 46), изображена проекциями А₁В₁С₁, А₂В₂С₂ и А₃В₃С₃. При этом горизонтальная и профильная проекции изображаются отрезками прямых линий, а фронтальная – треугольником, который равняется истинной величине треугольника АВС, т.к. он в пространстве занимает параллельное положение относительно плоскости проекций П_2.

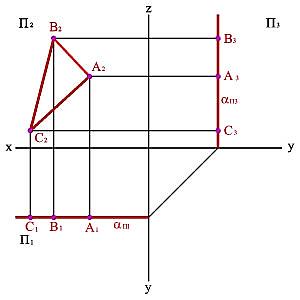
Рисунок 46 – Фронтальная плоскость уровня

Профильная плоскость уровня– плоскость, параллельная профильной плоскости проекций и перпендикулярна одновременно горизонтальной и фронтальной плоскостям проекций.

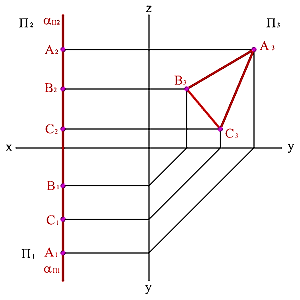
Профильная плоскость, заданная треугольником АВС (рисунок 47), изображена проекциями А₁В₁С₁, А₂В₂С₂ и А₃В₃С₃. При этом горизонтальная и фронтальная проекции изображаются отрезками прямых линий, а профильная – треугольником, который равняется истинной величине треугольника АВС, т.к. он в пространстве занимает параллельное положение относительно плоскости проекций П_3.

Рисунок 47 – Профильная плоскость уровня

Образование и обзор кривых поверхностей

(линейчатые и нелинейчатые, развертываемые и неразвертываемые)

Общие сведения. Термины и определения

Поверхностиширокоприменяютсявразличныхобластях техники,архитектуры,строительстваит.д.Начертательнаягеометрия изучаеткривыеповерхности,способыихобразования,позиционные, метрические и другие их свойства.

Подповерхностьюподразумеваютнепрерывноемножествоточек, еслимеждукоординатамиточекможетбытьустановленазависимость, определяемая уравнением вида F (x, y, z) = 0, где F (x, y, z) – многочлен n-ой степени или в форме какой-либо трансцендентной функции.

При кинематическом способе задания поверхность рассматривается как совокупность всех положений движущейся линии. Линию, производящую поверхность, в каждом ее положении называют образующей. Образующая линияможетбытьпрямойиликривой.

Поверхность на чертеже может быть задана ее определителем, очерком, каркасом.

Определительповерхности –это совокупность условий, однозначно определяющих данную поверхность. Определительповерхности состоит из двух частей: геометрической, задающей форму образующей и направляющей, и алгоритмической, определяющей условия перемещения или же изменения образующей.

Очеркповерхности – это линия пересечения плоскости проекций с проецирующей на данную плоскость проекций цилиндрической поверхностью, огибающей заданную поверхность.

Каркасповерхности – это совокупность линий, принадлежащих поверхности.

Способы задания поверхности на чертеже

Аналитический

Поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют некоторому заданному уравнению вида F(x,y,z)=0 (рисунок 68 а, б, в).

Рисунок 68 – Аналитические поверхности

А – эллипсоид

В – гиперболический цилиндр

Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать свойства поверхности.

Кинематический

Кинематическую поверхность можно рассматривать как непрерывную совокупность последовательных положений линии, перемещающейся в пространстве по некоторым неподвижным линиям.

Рассмотрим формирование конической поверхности (рисунок 69). Такая поверхность образована движением прямой образующей l, постоянно проходящей через точку S и во всех своих положениях пересекающей некоторую направляющую кривую m. Если направляющая m – окружность, каждая точка которой равноудалена от вершины S, образуется прямой круговой конус.

Рисунок 69 – Образование конической поверхности

Каркасный

Поверхности, к которым нельзя применить математические закономерности или поверхности с произвольными образующими называются скульптурными или поверхностями произвольных форм (рисунок 70). Такие поверхности обычно задают достаточно плотной сетью линий и точек, принадлежащих этим поверхностям.

Рисунок 70 – Скульптурная поверхность

Одним из наиболее распространенных в промышленности методов конструирования поверхностей является метод конструирования с помощью непрерывного каркаса. Метод каркасного конструирования используется при изготовлении кузовов автомобилей, самолетов и в судостроении, для выполнения штампов при изготовлении поверхностей из листового материала, в топографии, горном и дорожном деле.

Образование и обзор кривых поверхностей

(линейчатые и нелинейчатые, развертываемые и неразвертываемые)

В зависимости от формы образующей и закона ее перемещения в пространстве поверхности можно разделить на отдельные группы.

Линейчатые поверхности – поверхности, которые могут быть образованы с помощью прямой линии.

Нелинейчатые поверхности – поверхности, которые могут быть образованы только с помощью кривой линии.

Развертывающиеся поверхности – поверхности, которые после разреза их по образующей могут быть совмещены с плоскостью без наличия разрывов и складок.

Неразвертывающиеся поверхности – поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок.

Поверхности с постоянной образующей – поверхности, образующая которых не изменяет своей формы в процессе образования поверхности.

Поверхности с переменной образующей – поверхности, образующая которых изменяется в процессе образования поверхности.

1.6.2 Многогранники: правильные и полуправильные.
Их сечения проецирующими плоскостями

Многогранникаминазываютсятела,ограниченные плоскими n-угольниками,которыеназываютсягранями.Линиипересеченияграней называютсяребрами,точкипересеченияребер – вершинами.Длявсех многогранников справедлива формула Эйлера: сумма граней и вершин за минусом числа ребер есть величина постоянная:Г + В – Р = 2.

На рисунке71 приведена классификация многогранников. Большую группумногогранниковсоставляютправильныеиполуправильные многогранники. Правильные многогранники характеризуютсяодинаковоправильнымигранями, одинаковымчисломребер,сходящихсяввершинах,иодинаковыми многогранными углами при вершинах. Полуправильные многогранники – это правильные многогранники со срезанными вершинами.

Выпуклыми многогранникаминазываютсямногогранники, располагаемые по одну сторону каждой грани. Если это не соблюдается, то многогранники называются вогнутыми или выпукло-вогнутыми.

Приведемпримерынекоторыхправильныхмногогранников. Тетраэдр – эточетырехгранник,всеграникоторогоравносторонние треугольники.Гексаэдр (куб) – шестигранник,всеграникоторого квадраты.Октаэдр – восьмигранник,всеграникоторогоравносторонние треугольники.Додекаэдр – двенадцатигранник,всеграникоторого правильныепятиугольники.Икосаэдр – двадцатигранник,всеграни которого равносторонние треугольники.

Рисунок 71– Классификация многогранников

Наиболее распространенными в технике многогранниками являются правильныеинеправильные,прямыеинаклонные призмы ипирамиды. Призмойназываетсямногогранник,воснованияхкоторогонаходятся плоские n-угольники,аостальныеграниявляютсявобщемслучае параллелограммами (рисунок 72).Пирамидойназываетсямногогранник,восновании которого находится плоский n – угольник, а боковыми гранями являются треугольники с общей вершиной (рисунок 73).

Рисунок 72 –Изображение призмы (прямая и наклонная)

Рисунок 73 – Изображение пирамиды

Наэпюремногогранникизадаютсяпроекциямиребер,так называемойсеткой ребер.Поверхностьмногогранниковсчитается геометрически непрозрачной, в связи с чем на эпюре следует определить видимость ребер методом конкурирующих точек (прямых). На рисунке 74показанпримерзаданиямногогранниковнаэпюреиопределения видимости ребер.

Рисунок 74 – Задание многогранника на эпюре

Поверхности вращения. Примеры поверхностей вращения

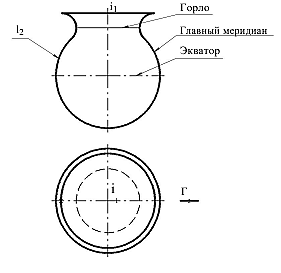
В числе кривых поверхностей – линейчатых и нелинейчатых – имеютсяширокораспространенныевпрактикеповерхностивращения.Поверхностью вращения называютповерхность,полученнуюотвращения какой-либо образующей линии l вокруг неподвижной прямой i– оси поверхности (рисунок 79).

Рисунок 79 – Поверхность вращения

При вращении вокруг оси каждая точка образующей l описывает окружность, которую называют параллелью поверхности вращения. Плоскости параллелей перпендикулярны оси поверхности. Наибольшую из параллелей поверхностивращенияназываютэкваторомповерхности,анаименьшую – горлом (шейкой).

Линии, получаемые при пересечении поверхности вращения плоскостями, проходящими через ось, называют меридианами поверхности. Меридиан, расположенный во фронтальной плоскости Г, называется главным меридианом.

Различаютповерхностивращенияспрямолинейнойикриволинейной образующей.

К поверхностям вращения с прямолинейной образующей относятся цилиндрическая и коническая поверхности вращения.

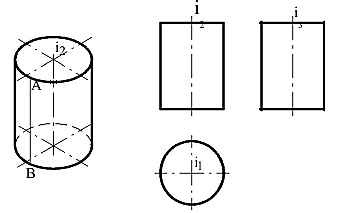
Цилиндрическойповерхностьювращенияназываетсяповерхность, образованнаяпрямойлинией(образующей),которая перемещается, оставаясь параллельной оси вращения. Боковая поверхность прямого кругового цилиндра (рисунок 80) образована движением отрезка АВ вокруг вертикальной оси i.

Рисунок 80 – Цилиндрическая поверхность вращения

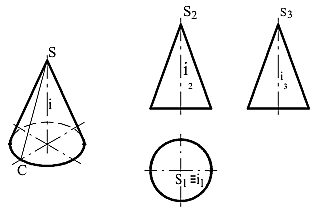
Коническая поверхность вращения представляет собой поверхность, образующая прямая которой пересекает ось вращения в точке, называемой вершинойконуса.Боковаяповерхностьпрямого кругового конуса (рисунок 81) образованавращениемобразующейSCвокругосиконусапо направляющей – окружности.

Рисунок 81 – Коническая поверхность вращения

Сферой называется поверхность, образованная вращением окружности вокруг одного из ее диаметров. На все плоскости проекций сфера проецируется в круг с радиусом, равным радиусу сферы (рисунок 82).

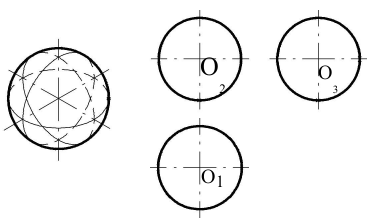
Эллипсоидом вращения называется поверхность