Лекция 2. ПРЯМАЯ И ПЛОСКОСТЬ НА ЭПЮРЕ МОНЖА
2.1. Задание прямой на эпюре.
2.2. Характеристика прямых.
2.3. Определение длины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций.
2.4. Взаимное расположение прямых.
2.5. Способы задание плоскости на эпюре.
2.6. Характеристика плоскостей.
2.7. Контрольные вопросы.
Задание прямой на эпюре
Чтобы построить прямую на эпюре необходимо на прямой взять две точки и спроецировать их на плоскости проекций (рис. 26). Затем проведя прямые через одноименные проекции точек получим проекции прямой.
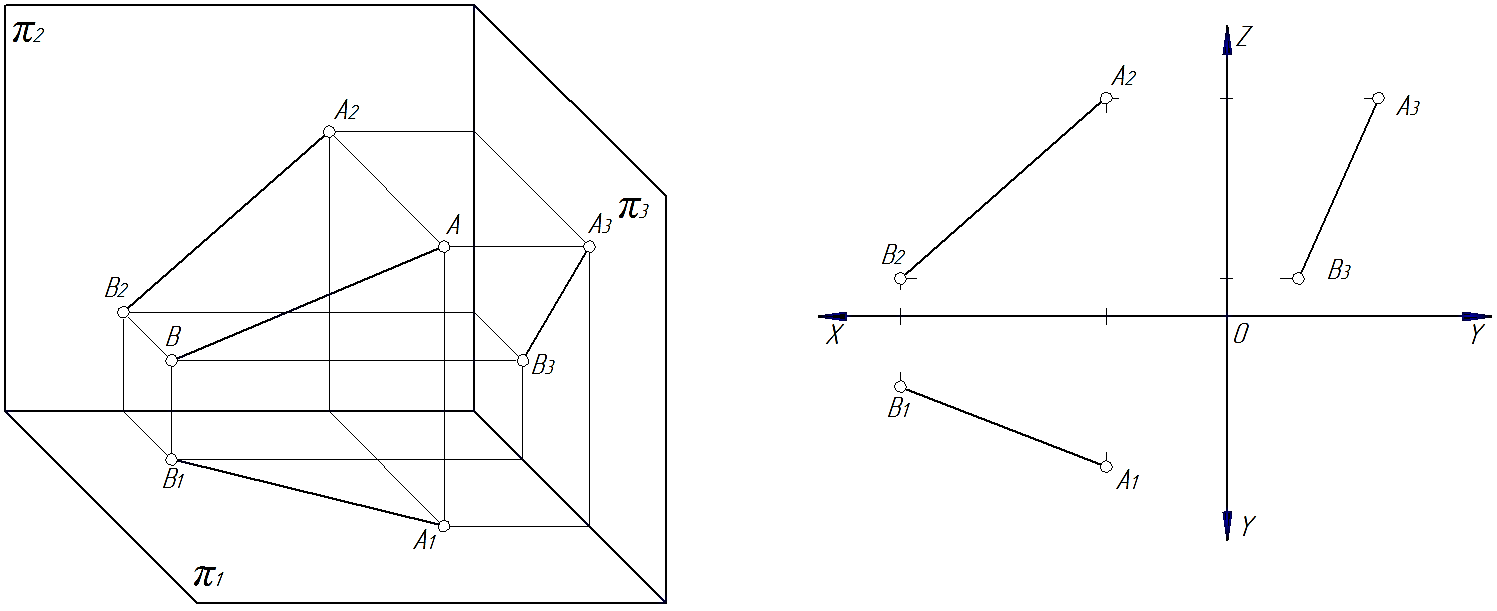
Рис. 26
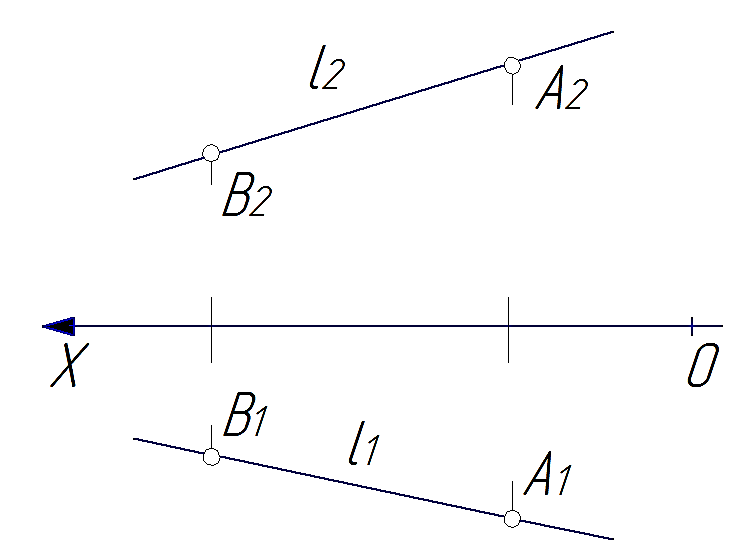 Рис. 27 Рис. 27 |
В общем случае прямые в пространстве могут задаваться (рис. 27) двумя точками (точки А и В), отрезком ([АВ]) или точкой и направлением прямой (например, точкой А и условиями, характеризующими направление прямой).
Примечание. В последующем все эпюры будут выполнятся методом двух изображений и только при необходимости будет использоваться полное проецирование (метод трех изображений).
Характеристика прямых
Все прямые пространства подразделяются на прямые общего и частного положений.
Прямая общего положения. Прямая общего положения не параллельны и не перпендикулярны ни одной из плоскостей проекций.
Примеры таких прямых показаны на рис. 26 и 27.
Особенностью изображения этих прямых является то, что на эпюре проекции прямой составляют с осями проекций произвольные углы и поэтому величина каждой проекции меньше истинной величины самой прямой (рис. 26).
Прямая частного положения. Прямые, параллельные или перпендикулярные плоскостям проекций называют прямыми частного положения.
Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня.
1. Прямые, параллельные горизонтальной плоскости проекций; называют горизонтальными или горизонталями h (рис. 28).
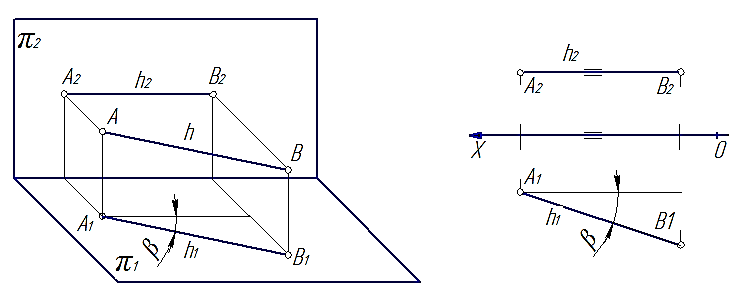
Рис. 28
Характерным признаком таких прямых на эпюре является то, что их фронтальные проекции параллельны оси 0Х.
2. Прямые, параллельные фронтальной плоскости проекций; называют фронтальными или фронталями f (рис. 29).
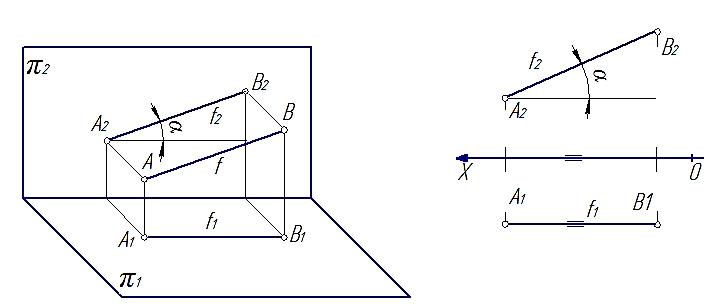
Рис. 29
Характерным признаком таких прямых на эпюре является то, что их горизонтальные проекции параллельны оси 0Х.
3. Прямую, параллельную профильной плоскости проекций, называют профильной р (рис. 30).
Характерным признаком таких прямых на эпюре является то, что их горизонтальные и фронтальные проекции перпендикулярны оси 0Х.
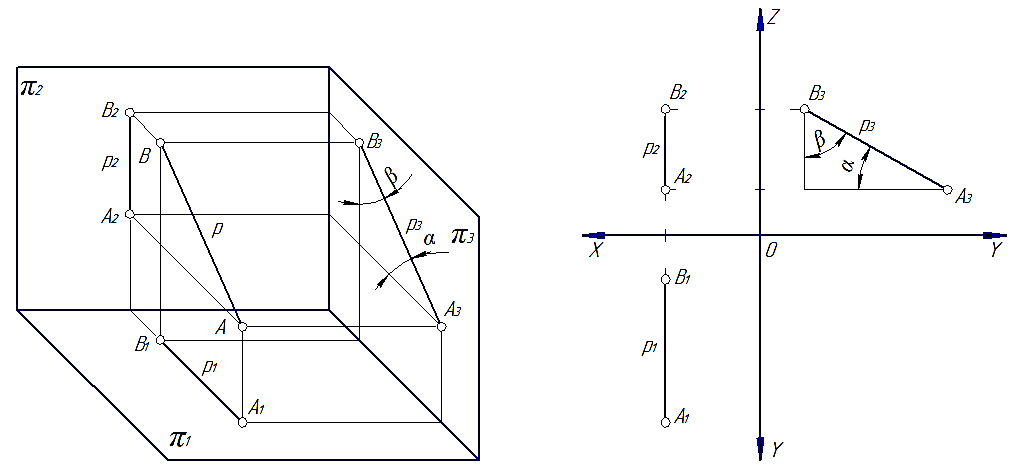
Рис. 30
Следует отметить, что каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона a и b, которые эта прямая образует с двумя другими плоскостями проекций, так же будут проецироваться на эту плоскость без искажения.
Так на рис. 28 проекция [A1B1]=[AB], а угол b – угол наклона отрезка [AB] к плоскости π2. На рис. 29 проекция [A2B2]=[AB], а угол a – угол наклона отрезка [AB] к плоскости π1. На рис. 30 видно, что все проекция [A2B2]=[AB], а углы a и b – углы наклона отрезка [AB] к плоскостям π1 и π1 соответственно.
Прямые уровня могут принадлежать плоскостям проекций. Такие прямые называют нулевыми горизонталями, нулевыми фронталями и нулевыми профильными прямыми.
Прямые, перпендикулярные к одной из плоскостей проекций называются проецирующими:
1) горизонтально-проецирующая – прямая l, перпендикулярная к горизонтальной плоскости проекций (рис. 31);
2) фронтально-проецирующая – прямая m, перпендикулярная к фронтальной плоскости проекций (рис. 32);
3) профильно-проецирующая – прямая n, перпендикулярная к профильной плоскости проекций (рис. 33).
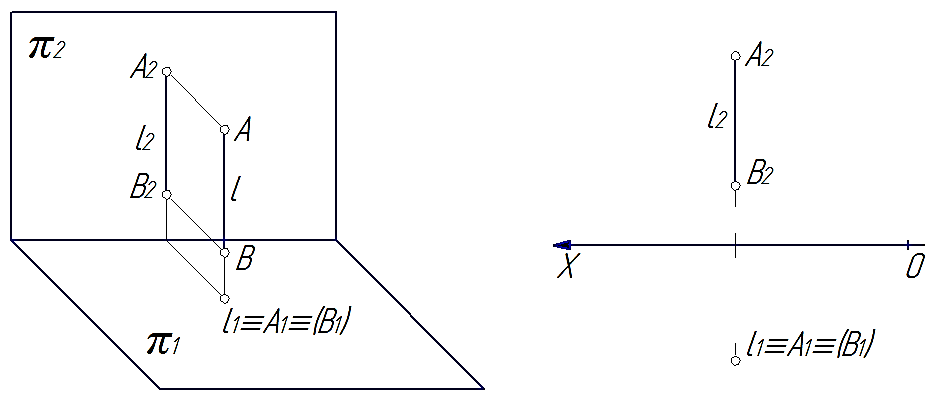
Рис. 31
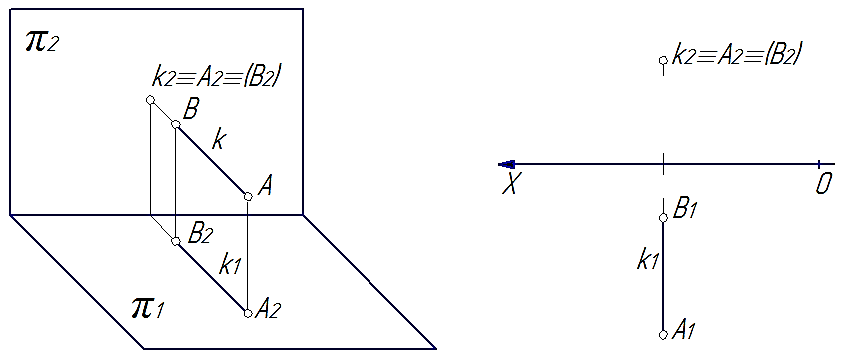
Рис. 32
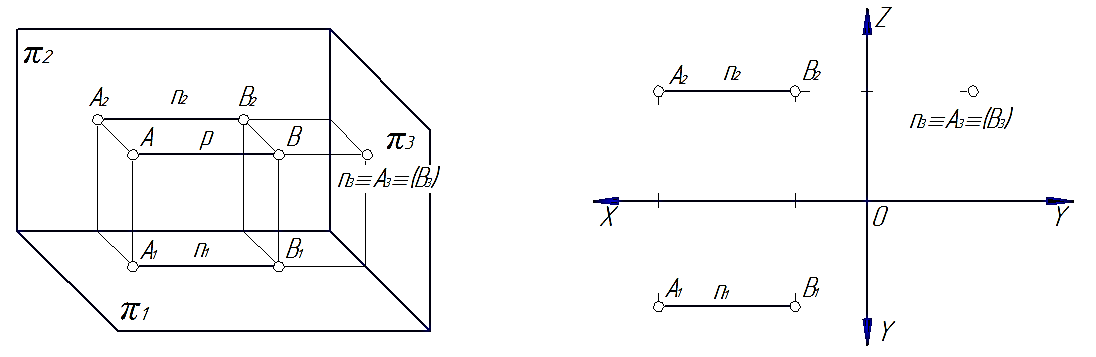
Рис. 33
На рис. 31, 32 и 33 видно, что проекции прямых, перпендикулярных к плоскостям проекций, на этих плоскостях представляют собой точки, а на тех плоскостях, которым прямые параллельны, проекции прямых будут перпендикулярны к осям и равны по величине самим прямым.
2.3. Определение длины отрезка прямой общего положения
и углов наклона прямой к плоскостям проекций
Определения натуральной величины отрезка прямой общего положения осуществляется путем построения на эпюре прямоугольный треугольника, одним катетом которого является проекция отрезка на какую-либо плоскость проекций, а величина другого катета равна разности расстояний концов отрезка от этой плоскости проекций. Натуральная величина отрезка прямой будет равна гипотенузе этого треугольника. Угол между катетом–проекцией и гипотенузой равен углу наклона отрезка к этой плоскости проекций.
На рис. 34 показано проецирование отрезка [АВ]. Через точку А проведена прямая АВ0, параллельная горизонтальной проекции отрезка А1В1. В полученном прямоугольном треугольнике АВВ0 катеты АВ0 равен проекции А1В1, а ВВ0 равен разности расстояний концов отрезка от плоскости проекций π1 (DZ). Гипотенуза этого треугольника равна длине отрезка [АВ]. Угол a в треугольнике АВВ0 является углом наклона отрезка прямой [АВ] к плоскости π1.
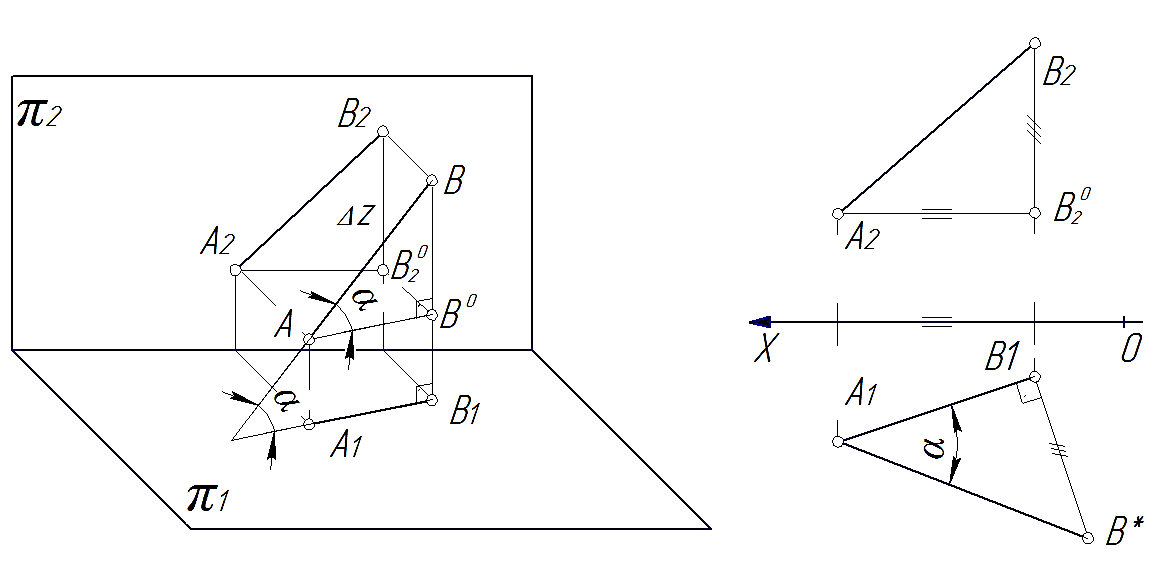
Рис. 34
Для определения угла наклона b отрезка прямой [АВ] к фронтальной плоскости проекций π2 строят прямоугольный треугольник (рис. 35) аналогичным путем, только за катеты принимаются проекция отрезка А2В2 и разность расстояний концов отрезка от плоскости проекций π2 (∆у).
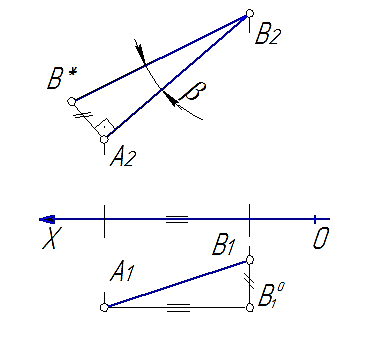
Рис. 35
