Перпендикулярность прямой и плоскости.

94. Провести через точку А перпендикуляр к плоскости, заданной прямыми АВ и АС (рис. 207).

Рис. 207

Решение

Известно, что горизонтальная проекция перпендикуляра к плоскости перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция 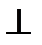к фронтальной проекции фронтали плоскости. На чертеже (рис. 207) АВявляется фронталью, а АС – горизонталью. Поэтому проводим через точку A₁ прямую n₁ 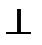A₁C₁, а через А₂ – прямую n₂ 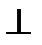А₂В₂. Прямая n (n₁, n₂) – искомый перпендикуляр к плоскости.

95. Провести через вершину А треугольника ABC перпендикуляр к его плоскости (рис. 208).

Рис. 208

Решение.Проведём в плоскости треугольника ABC горизонталь h (h₁,h₂) через точку A (A₁, A₂) и фрональ f (f₁, f₂) через точку C (C₁, C₂). Далее через точку А проведём n₁ 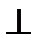h₁ и n₂ 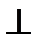f₂.

96.В точке А треугольника ABC восставить к его плоскости перпендикуляр и отложить на нем заданную величину h.

Решение

Восставляем в точке А перпендикуляр к плоскости ABC и откладываем на нем заданную величину h.

97.Определить расстояние от точки D до плоскости ABC(рис. 209).

Натуральная Величина DK

Рис. 209

Решение

Рассмотрим поэтапное решение этой комплексной задачи. Чтобы найти расстояние от точки Dдо плоскости ABC,необходимо:

1) Опустить из точки D на плоскость ABC перпендикуляр n. Так как n₁ 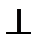h₁, а n₂ 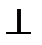f₂, то прежде всего проводим в плоскости ABC линии уровня: горизонталь h (h₁, h₂) и фронталь f (f₁, f₂) (см. рис. 208).

2) Далее (рис. 209, б) из точки D₂ проводим n₂ 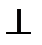f₂ и из точкиD₁ проводим n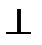₁ h₁.

3) Находим точку пересечения K (K₁,K₂) перпендикуляра n с плоскостью ABC и определяем видимость (рис. 209, в).

4) Определяем истинную величину отрезка DК способом прямоугольного треугольника (см. рис. 201).

98.Через точку А провести перпендикуляр к плоскости, заданной прямыми АВ и АС и отложить на нем отрезок, равный l (рис. 210).

Рис. 210

99.Построить проекции пирамиды, основанием которой является треугольник ABC,а ребро SA определяет высоту hпирамиды (рис. 211).

Решение

(см. задачи 95 и 96). Найдя проекции S₁, S₂ вершины S пирамиды, соединяем их с проекциями точек А, В, С.

Рис. 211

100.Построить точку, симметричную данной точке М относительно
плоскости треугольника АВС (рис. 212).

Рис. 212

101.Через точку А (А₁, А₂) провести плоскость, перпендикулярную прямой: а) h (h₁, h₂); б) f (f₁, f₂); в) a (a₁, a₂) (рис. 213).

Рис. 213

102. Найти расстояние от точки А до плоскости SCD пирамиды SBCD (рис. 214).

Рис. 214

103. Построить геометрическое место точек, удаленных от DАВС на расстояние l (рис. 215).

Рис. 215

104.На прямой CD найти точку, равноудаленную от концов отрезка АВ.

105.На прямой k найти точку, отстоящую от плоскости АВС на расстоянии l= 40 мм.

106. Построить проекции прямой треугольной призмы, если известны ее основание АВС и ребро h = 60 мм.

107. Построить проекции пирамиды, если известно ее основание АВС и высота h = 60 мм, опущенная в центр тяжести этого треугольника.

108. Через точку А (3;4;5) провести прямую, проходящую параллельно плоскости XОZ и перпендикулярную прямой АВ, где В (-3;-4;-5).

Развертки поверхностей

109.Дан тетраэдр SАВС и две точки M и N (рис. 216). Построить кратчайшую линию на поверхности тетраэдра SАВС, соединяющую точки M и N, если точка М на фронтальной проекции видима.

Рис. 216

110.Построить развертку поверхности призмы и определить на ней положение отрезка MN (M₁N₁) (рис. 217).

Рис. 217

111. Построить развёртку треугольной пирамиды DABC (рис. 218).

Рис. 218

Решение

Так как развёрткой многогранника является плоская фигура, полученная последовательным совмещением с плоскостью одной грани всех остальных граней, то задача сводится к нахождению натуральных величин граней DAB, DBC, DCA, ABC, что в свою очередь сводится к нахождению натуральных величин рёбер DA, DB и т.д. Определить натуральных длину ребра можно любым из рассматриваемых выше способов. Затем, пристраивая один треугольник к другому с помощью засечек циркуля, строим развёртку пирамиды (рис. 219).

На развёртке вершины 5, 6, 8 и т.д. пространственной ломаной линии находим с помощью засечек на натуральных величинах рёбер или прямых, на которых они лежат.

Рис. 219

112.Построить пирамиду SАВС по заданной ее развертке, если основание АВС параллельно плоскости П₁ (Рис. 220).

Рис. 220

113. Построить развертку поверхности усеченного конуса (рис. 221).

Рис. 221

114. Построить развертку конической части трубы (рис. 222).

Рис. 222

115. По заданной развертке цилиндрической поверхности вращения (рис. 223) построить ее ортогональные проекции, расположив ось перпендикулярно плоскости П₁.

Рис. 223

116. Построить развертку вытяжной трубы (рис. 224).

Рис. 224