Поверхность называется алгебраической, если соответствующее ей уравнение является алгебраическим многочленом.
Порядком поверхности с алгебраической точки зрения является наивысшая степень соответствующего ей алгебраического уравнения (рис. 3.1).
Порядком поверхности с геометрической точки зрения называется максимальное число точек пересечения произвольной прямой с этой поверхностью (включая мнимые точки).
| Уравнение сферы: x2 +y2 + z2 = R2 Поверхность второго порядка: N = 2 | 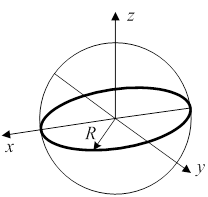 |
Рисунок 3.1
Кинематические поверхности образуются непрерывным перемещением в пространстве некоторой линии - (образующей) по определенному закону.
Поверхность образованная перемещением прямой линии называется линейчатой.
Закон перемещения образующей определяется направляющими, максимальное количество которых может быть три. Направляющие могут вырождаться в точку, прямую, в плоскость параллелизма.
Определитель поверхности Ф (Г) [А] - в геометрической части (Г) совокупность проекций постоянных геометрических элементов и алгоритм построения точек линий поверхности.
[А] - алгоритмическая часть одинакова для всех поверхностей: точка принадлежит поверхности, если она принадлежит некоторой линии принадлежащей этой поверхности.
Поверхность считается заданной, если относительно любой точки пространства можно однозначно решить вопрос о принадлежности точки этой поверхности.
На комплексном чертеже поверхности задаются проекциями своего геометрического определителя, а изображаются своим очерком, т.е. проекциями линии контура и линии обреза.
Призматическая поверхность
Призматическая поверхность- линейчатая поверхность, образованная параллельным перемещением прямой в пространстве (образующей) и пересекающей ломаную линию (направляющую).
Призматическая поверхность в пространстве и на чертеже задается своим определителем Ф (m; 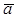 )[А](рис. 3.2).
)[А](рис. 3.2).
где m - направляющая;
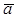 - направление перемещения образующей;
- направление перемещения образующей;
М Ì Ф - произвольная точка, принадлежащая поверхности призмы;
l || 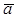 - образующая, проходящая через т. М;
- образующая, проходящая через т. М;
l É М и l ∩ m = 1 М2 задана произвольно  М2 Î l2 l2 || ā2 l2 ∩ m2 = 12 12 ® 11 и 11Î l1 l1 || ā1 М1 Î l1 М2 Î l2 l2 || ā2 l2 ∩ m2 = 12 12 ® 11 и 11Î l1 l1 || ā1 М1 Î l1 | 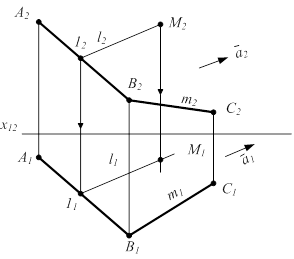 |
Рисунок 3.2
Т.к. М произвольная точка и вторая проекция ее построена, то теорема доказана.
Призма - геометрическая фигура, ограниченная замкнутой призматической поверхностью и двумя плоскостями (рис. 3.3).
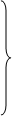 l ^ П1 l ^ П1  Г || П1 П1 Г || П1 П1 | 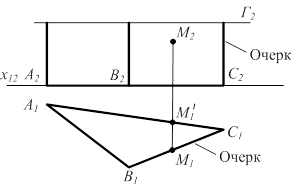 |
Рисунок 3.3
Пирамидальная поверхность
Пирамидальная поверхность - поверхность образованная непрерывным перемещением прямой, проходящей через фиксированную точку и пересекающей ломаную линию.
Пирамидальная поверхность задается в пространстве и на чертеже своим определителем Ф(S,m)[А], где S - вершина пирамиды; m – направляющая, ломаная линия (рис. 3.4).
Пирамидальная поверхность располагается по обе стороны от ее вершины, может быть замкнутой и незамкнутой.
М – произвольная точка, принадлежащая поверхности пирамиды.
Образующая l проходит через т.М, вершину S и пересекает направляющую m.
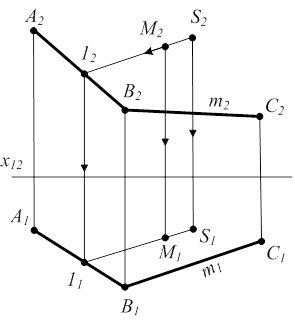
Рисунок 3.4
Пирамидой называется часть пространства, ограниченная пирамидальной поверхностью, а также вершиной и плоскостью или двумя плоскостями (рис. 3.5).
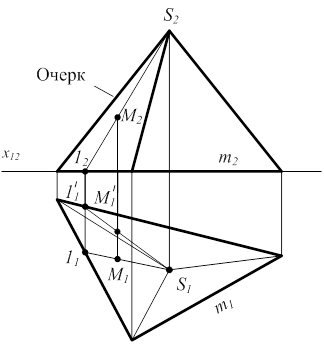
Рисунок 3.5
Поверхность вращения
Поверхность вращения - поверхность, образованная вращением некоторой кривой (образующей) вокруг прямой (оси вращения) (рис. 3.6).
S (i, l) [А]: i - ось вращения;  l - образующая; М Î S; аM - окружность вращения точки М; Г ^ i - параллели l - образующая; М Î S; аM - окружность вращения точки М; Г ^ i - параллели | 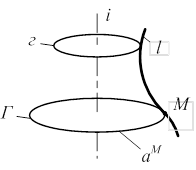 |
Рисунок 3.6
Параллель максимального радиуса вращения, если такая есть (у конуса ее нет) называется экватором.
Параллель минимального радиуса, если такая есть, называется горловой линией.
Цилиндрическая поверхность
Цилиндрическая поверхность - линейчатая поверхность, образованная параллельным перемещением прямой (образующей) в пространстве, пересекающей кривую линию (направляющую) (рис. 3.7).
S (a;m) [А]: 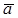 - направление перемещения образующей; m - направление перемещения образующей; m  - направляющая; М Î S; l Ì M и l || - направляющая; М Î S; l Ì M и l || 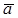 l ∩ m l ∩ m | 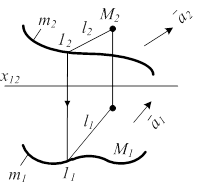 |
Рисунок 3.7
Цилиндрической поверхностью вращения называется поверхность, образованная вращением прямой линии параллельной оси вращения вокруг этой оси (рис. 3.8).
