Арифметический квадратный корень

Арифметическая прогрессия

Последовательность, у которой задан первый член a₁, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией:

a_n+1 = a_n + d, где d – разность прогрессии.

an = a1 + d(n – 1)	an = ak + d(n – k)
2an = an-1 + an+1	an + am = ak + al, если n + m = k + l

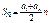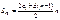Геометрическая прогрессия

Определение: Последовательность, у которой задан первый член b₁ ¹ 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q ¹ 0, называется геометрической прогрессией:

b_n+1 = b_n q, где q – знаменатель прогрессии.

bn = b1 qn – 1	bn = bk qn – k
bn2 = bn-1 bn+1	bn bm = bk bl, если n + m = k + l
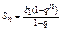	Бесконечно убывающая геометрическая прогрессия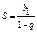

Степень

Определение

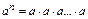, если n – натуральное число

a – основание степени, n - показатель степени

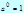
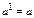
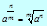
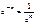
Формулы

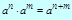
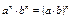
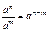
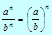
Арифметический квадратный корень

Определение

Арифметическим квадратным корнем из неотрицательного числа a - ( 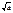) - называется неотрицательное число, квадрат которого равен a.

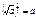
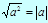
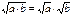
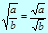
Корнем k–ой степени из a (k - нечетное) называется число, k-ая степень которого равна a.

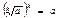
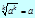
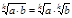
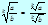
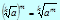
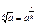
Квадратное уравнение:

ax² + bx + c = 0

Дискриминант: D = b² – 4ac

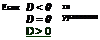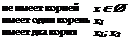Теорема Виета

Приведенное квадратное уравнение: x² + px + q = 0

x₁ + x₂ = - p

x₁ × x₂ = q

x₁+x₂ = -b/a

x₁× x₂ = c/a

Логарифм

Определение

Логарифмом числа по b основанию a называется такое число, обозначаемое 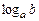, что .

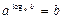a - основание логарифма (a > 0, a ¹ 1),

b - логарифмическое число ( b > 0)

Десятичный логарифм: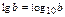

Натуральный логарифм: 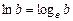где e = 2,71828

Формулы

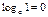
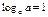
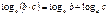
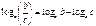
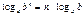
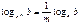
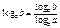
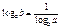
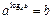
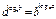
Дроби

Сложение

Деление с остатком:

	Признак	Пример
На 2	Числа, оканчивающиеся нулём или четной цифрой	…….6
На 4	Числа, у которых две последние цифры нули или выражают число, делящееся на 4.	……12
На 8	Числа, у которых три последние цифры нули или выражают число, делящееся на 8.	…..104
На 3	Числа, сумма цифр которых делится на 3.
На 9	Числа, сумма цифр которых делится на 9.
На 5	Числа, оканчивающиеся нулём или цифрой 5.	…….5
На 25	Числа, у которых две последние цифры нули или выражают число, делящееся на 25.	……75
На 10	Числа, оканчивающиеся нулём.	……0

Формуладеления с остатком: n = m×k + r, где n – делимое, m - делитель, k - частное, r – остаток: 0 £ r < m   Пример: Любое число можно представить в виде: n = 2k + r, где r = {0; 1} или n = 4k + r, где r = {0; 1; 2; 3}

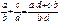
Вычитание

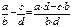
Умножение

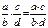
Деление

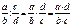
Составная дробь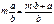

Делимость натуральных чисел:

Пусть n : m = k, где n, m, k – натуральные числа.

Тогда m – делитель числа n, а n – кратно числу m.

Число n называется простым, если его делителями являются

только единица и само число n.

Множество простых чисел: {2; 3; 5; 7; 11; 13; . . .; 41; 43; 47 и т.д.}

Числа n и m называются взаимно простыми, если у них нет общихделителей, кроме единицы.

Десятичные числа:

Стандартный вид: 317,3 = 3,173× 10² ; 0,00003173 = 3,173× 10^-5

Форма записи: 3173 = 3× 1000 + 1× 100 + 7× 10 + 3

Модуль

Формулы Определение

· ½x½ ³ 0

· ½x - y½ ³ ½x½ - ½y½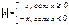

· ½-x½=½x½

· ½x × y½ = ½x½ × ½y½

· ½x½ ³ x

· ½x : y½ =½x½ : ½y½

· ½x + y½ £ ½x½ + ½y½

½x½² = x²

Неравенства

Определения:

Неравенством называется выражение вида:

a < b (a £ b), a > b (a ³ b)

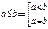
Основные свойства:

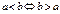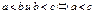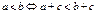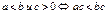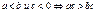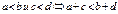Периодическая дробь

Правило:

Признаки делимости чисел:

Проценты

Определение:

Процентом называется сотая часть от числа. 1%A = 0,01A

Основные типы задач на проценты:

Сколько процентов составляет число A от числа B?

B - 100%

A - x%

Сложные проценты.

Число A увеличилось на 20%, а затем полученное число уменьшили на 25%.

Как, в итоге, изменилось исходное число?

1) A₁ = (100% + 20%)A = 120%A = 1,2A

2) A₂ = (100% - 25%)A₁=75%A₁ = 0,75A₁ = 0,75×1,2A = 0,9A = 90%A

3) A₁ – A = 90%A – 100%A = -10%A

Þ Ответ: уменьшилось на 10%. Изменение величины.

Как изменится время, если скорость движения увеличится на 25%?

Þ Ответ: уменьшится на 20%

Þ Ответ: уменьшится на 20%

Уравнение движения

Пусть - уравнение движения материальной точки, где S – путь, t – время движения.

Тогда: ,

где – скорость, - ускорение.

Определенный интеграл

Тригонометрия

Основные триг. формулы

Þ

Þ

Формулы суммы функций

Формулы суммы аргументов:

Формулы двойного аргумента

Универсальная подстановка

Уравнения с синусом

Частные формулы:

Общая формула:

Обратные триг функции

Функция	Свойства
Область определения	Множество значений
arccosx		[0; p]
arcsinx		[-p/2; p/2]
arctgx		(-p/2; p/2)
arcctgx		(0; p)

Геометрия

Теорема косинусов, синусов

Теорема косинусов:

Теорема синусов:

Площадь треугольника

Средняя линия

Средняя линия – отрезок, с соединяющий середины двух с сторон треугольника.

Средняя линия параллельна т третьей стороне и равна е её половине:

Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного

Равносторонний треугольник

треугольник, у которого все стороны равны.

v Все углы равны 60⁰.

v Каждая из высот является одновременно биссектрисой и медианой.

v Центры описанной и вписанной окружностей совпадают.

v Радиусы окружностей:

Площадь

Равнобедренный треугольник

треугольник, у которого две стороны равны.

1.Углы, при основании треугольника, равны

2.Высота, проведенная из вершины, является б биссектрисой и медиан

bc

Прямоугольный треугольник

v Теорема Пифагора: Площадь:

v Тригонометрические соотношения:

v Центр описанной окружности лежит на середине гипотенузы.

v Радиусы окружностей:

v Высота, опущенная на гипотенузу:

v Катеты:

Биссектриса

Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.

· Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: a_b : a_c = b : c

· Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.

·

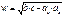
Конус

H

R

S_бок.= pR(R+L)

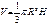
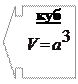
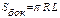
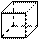Усеченный конус

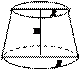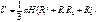
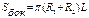
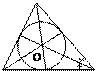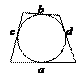Вписанная окружность

· Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.

· Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой:

a + b = c + d

Описанная окружность

Касательная, секущая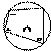

·

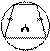
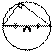
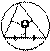
· Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.

· Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.

· Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.

· Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой: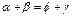

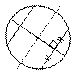
Длина окружности, площадь

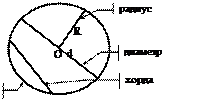
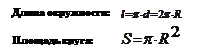
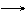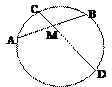Хорда

Хорда – отрезок, соединяющий две точки окружности.

· Диаметр, делящий хорду пополам, перпендикулярен хорде.

· В окружности равные хорды равноудалены от центра окружности.

· Отрезки пересекающихся хорд связаны равенством:

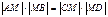
Шар

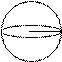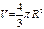
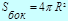
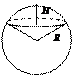Шаровой сектор

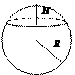
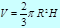
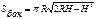
Шаровой сегмент

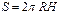
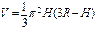
Центральный, вписанный угол

Сектор

Касательная, секущая

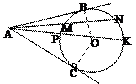Касательная – прямая, имеющая с окружностью одну общую точку.

Секущая – прямая, имеющая с окружностью две общие точки.

X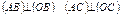

X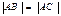

X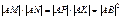

Призма

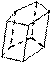
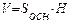
Прямая

Призма

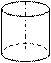
Цилиндр

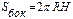
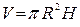
Медиана

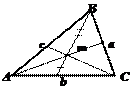Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

· Медианы треугольника точкой их пересечения делятся в отношении 2:1 (считая от вершины треугольника).

· Медиана делит треугольник на два треугольника с равными площадями.

Правильная пирамида

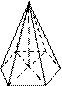Правильная пирамида

пирамида, у которой в основании и правильный многоугольник, а вершина с м проецируется в центр основания.

М Все боковые рёбра равны между м м собой и все боковые грани – равные м равнобедренные треугольники.

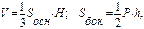
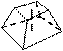Усеченная пирамида

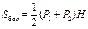
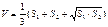
Скалярное произведение

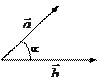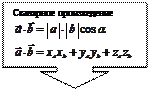
Сумма, разность векторов

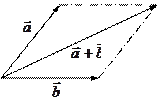
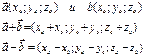
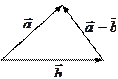
Углы на плоскости

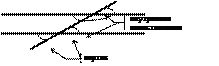Координаты вектора

Координаты вектора: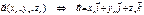

Длина вектора: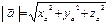

Умножение вектора на число: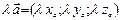

Правильный многоугольник

Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.

ü Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.

ü Сторона правильного n–угольника:

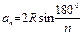
Площадь правильного n–угольника: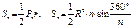

Квадрат

Квадрат:

Прямоугольник, у которого все стороны равны, называется квадратом.

ü 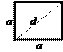Диагональ квадрата 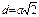Площадь: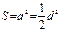

Ромб

Ромб:

Параллелограмм, все стороны которого равны называется ромбом.

ü Диагональ ромба является его осью симметрии. Диагонали взаимно перпендикулярны. Диагонали являются биссектрисами углов.

ü Площадь: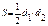

Параллелограмм

Параллелограмм:

Четырёхугольник, у которого противоположные стороны попарно параллельные называется параллелограммом.

ü Середина диагонали является центром симметрии.

ü Противоположные стороны и углы равны.

ü Каждая диагональ делит параллелограмм на два равных треугольника.

ü Диагонали делятся точкой пересечения пополам: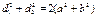

ü Площадь: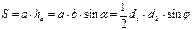

Арифметическая прогрессия

Последовательность, у которой задан первый член a₁, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией:

a_n+1 = a_n + d, где d – разность прогрессии.

an = a1 + d(n – 1)	an = ak + d(n – k)
2an = an-1 + an+1	an + am = ak + al, если n + m = k + l

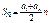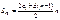Геометрическая прогрессия

Определение: Последовательность, у которой задан первый член b₁ ¹ 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q ¹ 0, называется геометрической прогрессией:

b_n+1 = b_n q, где q – знаменатель прогрессии.

bn = b1 qn – 1	bn = bk qn – k
bn2 = bn-1 bn+1	bn bm = bk bl, если n + m = k + l
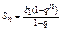	Бесконечно убывающая геометрическая прогрессия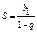

Степень

Определение

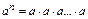, если n – натуральное число

a – основание степени, n - показатель степени

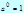
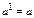
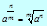
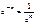
Формулы

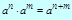
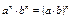
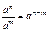
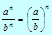
Арифметический квадратный корень

Определение

Арифметическим квадратным корнем из неотрицательного числа a - ( 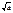) - называется неотрицательное число, квадрат которого равен a.

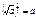
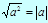
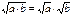
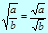
Корнем k–ой степени из a (k - нечетное) называется число, k-ая степень которого равна a.

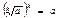
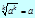
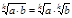
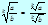
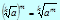
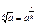
Квадратное уравнение:

ax² + bx + c = 0

Дискриминант: D = b² – 4ac

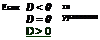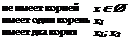Теорема Виета

Приведенное квадратное уравнение: x² + px + q = 0

x₁ + x₂ = - p

x₁ × x₂ = q

x₁+x₂ = -b/a

x₁× x₂ = c/a

Логарифм

Определение

Логарифмом числа по b основанию a называется такое число, обозначаемое 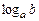, что .

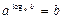a - основание логарифма (a > 0, a ¹ 1),

b - логарифмическое число ( b > 0)

Десятичный логарифм: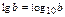

Натуральный логарифм: 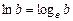где e = 2,71828

Формулы

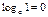
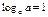
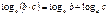
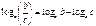
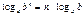
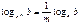
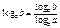
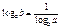
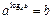
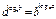
Дроби

Сложение

Деление с остатком:

	Признак	Пример
На 2	Числа, оканчивающиеся нулём или четной цифрой	…….6
На 4	Числа, у которых две последние цифры нули или выражают число, делящееся на 4.	……12
На 8	Числа, у которых три последние цифры нули или выражают число, делящееся на 8.	…..104
На 3	Числа, сумма цифр которых делится на 3.
На 9	Числа, сумма цифр которых делится на 9.
На 5	Числа, оканчивающиеся нулём или цифрой 5.	…….5
На 25	Числа, у которых две последние цифры нули или выражают число, делящееся на 25.	……75
На 10	Числа, оканчивающиеся нулём.	……0

Формуладеления с остатком: n = m×k + r, где n – делимое, m - делитель, k - частное, r – остаток: 0 £ r < m   Пример: Любое число можно представить в виде: n = 2k + r, где r = {0; 1} или n = 4k + r, где r = {0; 1; 2; 3}

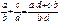
Вычитание

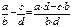
Умножение

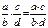
Деление

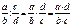
Составная дробь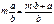

Делимость натуральных чисел:

Пусть n : m = k, где n, m, k – натуральные числа.

Тогда m – делитель числа n, а n – кратно числу m.

Число n называется простым, если его делителями являются

только единица и само число n.

Множество простых чисел: {2; 3; 5; 7; 11; 13; . . .; 41; 43; 47 и т.д.}

Числа n и m называются взаимно простыми, если у них нет общихделителей, кроме единицы.

Десятичные числа:

Стандартный вид: 317,3 = 3,173× 10² ; 0,00003173 = 3,173× 10^-5

Форма записи: 3173 = 3× 1000 + 1× 100 + 7× 10 + 3

Модуль

Формулы Определение

· ½x½ ³ 0

· ½x - y½ ³ ½x½ - ½y½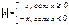

· ½-x½=½x½

· ½x × y½ = ½x½ × ½y½

· ½x½ ³ x

· ½x : y½ =½x½ : ½y½

· ½x + y½ £ ½x½ + ½y½

½x½² = x²

Неравенства

Определения:

Неравенством называется выражение вида:

a < b (a £ b), a > b (a ³ b)

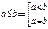
Основные свойства:
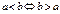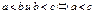
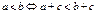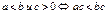
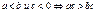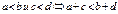