Расстоянием между двумя различными точками называется длина отрезка, соединяющего эти точки.

2) Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из точки к прямой.

Замечание:

1) Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости, то есть длина перпендикуляра, проведенного из произвольной точки одной из параллельных плоскостей к другой плоскости.

2) Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости, то есть длина перпендикуляра, проведенного из произвольной точки прямой к плоскости.

3) Расстоянием между скрещивающимися прямыминазывается расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.

2. 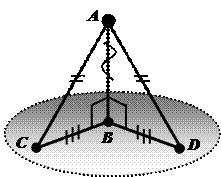Наклонные к плоскости, проведенные из одной точки, равны тогда и только тогда, когда равны их проекции на эту плоскость.

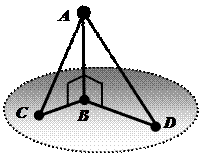Одна наклонная меньше другой наклонной, проведенной из этой же точки к плоскости, тогда и только тогда, когда проекция первой наклонной меньше проекции второй наклонной.

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

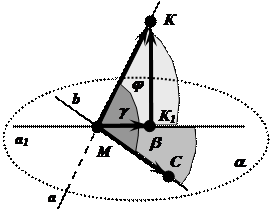Задача: Сравнить угол между наклонной а и её проекцией а₁ на плоскость a с углом между этой наклонной и произвольной прямой b, принадлежащей плоскости a .

Дано: ; ;

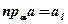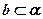
Сравнить: 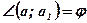и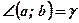

Решение:

; ;

; ;

;

;

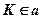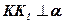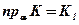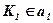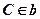
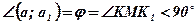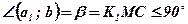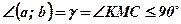
С помощью векторов выведем формулу, связывающую углы .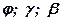

;

;

;

; ;

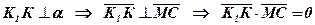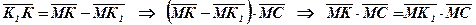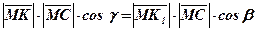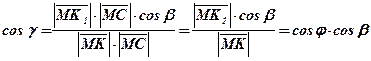
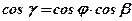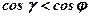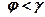
Вывод: Угол между наклонной к плоскости и её проекцией на эту плоскость есть наименьший из углов, образованных наклонной со всеми прямыми, лежащими в плоскости.

Определение: Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость: .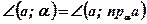

ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

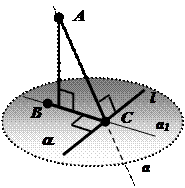Теорема: Для того чтобы прямая, принадлежащая плоскости, была перпендикулярна наклонной к этой плоскости, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной.

Необходимое условие:

Дано: 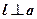Доказать: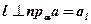

Доказательство:

; ; ;

; ; ;

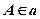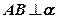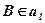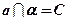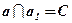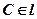Через точки А, В, С проходит единственная плоскость АВС. По признаку перпендикулярности прямой и плоскости прямая l перпендикулярна плоскости АВС:

1) 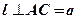по условию теоремы;

2) 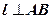, так как 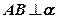, а значит, она перпендикулярна любой прямой, принадлежащей плоскости .

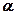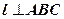, значит, прямая l перпендикулярна любой прямой, принадлежащей плоскости 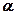. Следовательно, 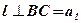, т. е. .

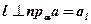Достаточное условие:

Дано: 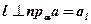Доказать: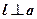

Доказательство:

По признаку перпендикулярности прямой и плоскости прямая l перпендикулярна плоскости АВС:

1. 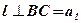по условию теоремы;

2. 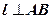, так как 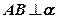, а значит, перпендикулярна любой прямой, принадлежащей плоскости .

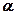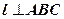, значит, прямая l перпендикулярна любой прямой, принадлежащей плоскости 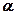. Следовательно, 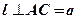, т. е. .

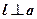Вывод: Чтобы доказать, что наклонная перпендикулярна прямой, лежащей в плоскости, надо показать, что её проекция перпендикулярна этой прямой.

Упражнения: