По уровню заработной платы
| Заработная плата, руб. x | Численность работников f |
| 15 950 16 790 17 000 | |
| Итого |
Решение:
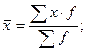
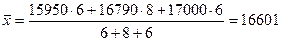(руб.)
Задача № 3.3.
Имеются данные о средней заработной плате по трем цехам предприятия:
| Цех | Среднемесячная заработная плата, руб. | Фонд заработной платы, руб. |
| 13 000 14 100 14 800 | 1 755 000 2 961 000 3 700 000 |
Рассчитать среднюю заработную плату в целом по предприятию.
Решение:
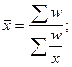
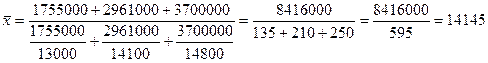
Задача № 3.4.
В таблице приведены данные о распределении предприятий района по размеру прибыли за последний отчетный год.
| Прибыль, млн. руб. | Количество предприятий |
| До 60 | |
| 60-80 | |
| 80-100 | |
| 100-120 | |
| 120 и более | |
| Итого |
Рассчитать средний размер прибыли в расчёте на одно предприятие.
Решение:
1) определяем середины интервалов:
50;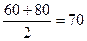 
; 
; 
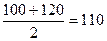; 130
2) определяем средний размер прибыли
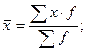
Задача № 4.1.Рассчитать показатели вариации для банков, сгруппированных по размеру прибыли:
| Размер прибыли (в млн. руб.) | Число банков 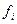 | Расчетные показатели | ||||
 |  |  |  |  | ||
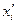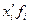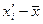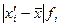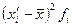| 3,7 – 4,6 (-) | 4,15 | 8,30 | -1,935 | 3,870 | 7,489 | |
| 4,6 – 5,5 | 5,05 | 20,20 | -1,035 | 4,140 | 4,285 | |
| 5,5 – 6,4 | 5,95 | 35,70 | -0,135 | 0,810 | 0,109 | |
| 6,4 – 7,3 | 6,85 | 34,25 | +0,765 | 3,825 | 2,926 | |
| 7,3 – 8,2 | 7,75 | 23,25 | +1,665 | 4,995 | 8,317 | |
Итого 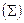 | 121,70 | 17,640 | 23,126 |
1) Найдем средний размер прибыли банков:
, 
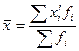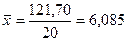млн. руб.
2) Найдем среднее линейное отклонение:
, 
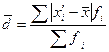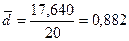млн. руб.
3) Найдем дисперсию:
, 
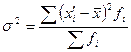4) Найдем среднее квадратическое отклонение:
, 
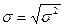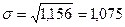млн. руб.
5) Найдем коэффициент вариации:
, 
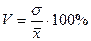Задача № 1.Опытные данные о значениях x и y представлены таблицей:
| x | ||||||
| y | -6 | -10 |
Определите:
1) Параметры a и b уравнения линейной регрессии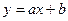 
, используя способ наименьших квадратов.
2) Линейный коэффициент корреляции.
Решение:
1) Составим расчётную таблицу:
| № п/п | x | y | xy | x2 | y2 |
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. | |||||
| 5. | -6 | -30 | |||
| 6. | -10 | -60 | |||
| Итого (Σ) | -43 |
2) Используя способ наименьших квадратов, составим систему нормальных уравнений и решим её.
; 
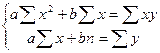
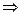
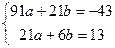3) Составим уравнение линейной корреляции.
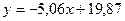
4) Рассчитаем линейный коэффициент корреляции
;
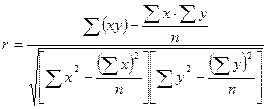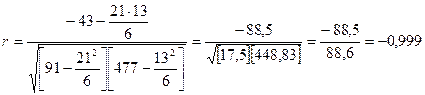
Задача № 2.
В таблице приведены сведения об успеваемости и посещаемости группы студентов:
| Группа | Пропуск, ч | Успеваемость, балл | Группа | Пропуск, ч | Успеваемость, балл |
| 2,4 | 3,4 | ||||
| 3,8 | 4,0 | ||||
| 3,7 | 2,8 | ||||
| 4,0 | 3,3 | ||||
| 2,1 | 4,0 | ||||
| 4,7 | 4,8 | ||||
| 3,0 | 3,6 | ||||
| 3,0 | 4,6 |
Определите:
1) параметры a и b уравнения линейной регрессии, связывающей показатели пропусков занятий x и успеваемости y:
2) тесноту связи между успеваемостью студентов и пропусками занятий;
Решение:
| Группа | x | y | xy | x2 | y2 |
| 2,4 | 192,0 | 5,76 | |||
| 3,8 | 22,8 | 14,44 | |||
| 3,7 | 59,2 | 13,69 | |||
| 4,0 | 8,0 | 16,00 | |||
| 2,1 | 71,4 | 4,41 | |||
| 4,7 | 22,09 | ||||
| 3,0 | 60,0 | 9,00 | |||
| 3,0 | 168,0 | 9,00 | |||
| 3,4 | 54,4 | 11,56 | |||
| 4,0 | 64,0 | 16,00 | |||
| 2,8 | 117,6 | 7,84 | |||
| 3,3 | 52,8 | 10,89 | |||
| 4,0 | 120,0 | 16,00 | |||
| 4,8 | 19,2 | 23,04 | |||
| 3,6 | 100,8 | 12,96 | |||
| 4,6 | 21,16 | ||||
| Всего | 57,2 | 1110,2 | 213,84 |
; 
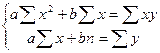
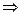
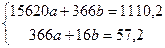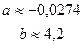
Уравнение регрессии: 
.
Коэффициент корреляции:
Задача № 7.2.1.Имеются данные о выпуске продукции на предприятии:
Таблица 1
| Вид продукции | Базисный период | Отчетный период | ||
| Цена единицы, тыс. руб. (p0) | Объем, тыс. единиц (q0) | Цена единицы, тыс. руб. (p1) | Объем, тыс. единиц (q1) | |
| А Б В | 13,2 20,5 17,6 | 13,0 20,0 17,5 |
Индекс стоимости продукции равен:
или 105,11%.
Задача № 7.2.2.
В отчётном периоде по сравнению с базисным цены выросли на 5 %, объём товарной массы увеличился на 2 %. Как изменился товарооборот?
Решение:
1) находим индекс цен: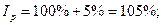 
2) находим индекс физического объема товарной массы: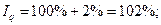 
3) находим индекс товарооборота: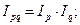 
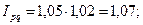
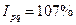
Товарооборот вырос на 7%.
Задача № 7.2.3.
Имеются следующие данные:
| Товар | Товарооборот магазина в феврале, тыс. руб. | Изменение физического объёма реализации товаров в марте по сравнению с февралем, % |
| p0 q0 | ||
| А Б В | 27 140 29 700 20 200 | +8,0 - 4,0 +3,0 |
Определите общий индекс физического объёма реализации.
Решение:
1) 
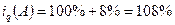
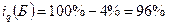
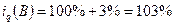
2) 
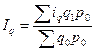
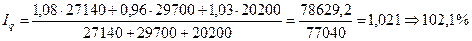
Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса. Например, индекс цен можно исчислить так:
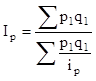, где 
.
Задача № 7.2.4.
Имеются следующие данные:
| Товар | Товарооборот, тыс. руб. | Изменение цены единицы товара во II квартале по сравнению с I кварталом, % | |
| I квартал | II квартал | ||
| p0q0 | p1q1 | ||
| А Б В | 1 700 2 300 1 900 | +8,0 +2,5 - 3,2 |
Определите общий индекс цен.
Решение:
1) 
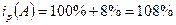
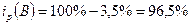
2) 
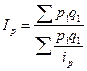
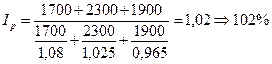
Задача № 7.3.1.
Имеются данные о выпуске однородной продукции по предприятиям АО:
| № предприятия АО | Выпуск продукции | Себестоимость единицы продукции, руб. | ||
| I квартал | II квартал | I квартал | II квартал | |
| тыс. ед. q0 | тыс. ед. q1 | z0 | z1 | |
| 7,0 6,0 | 8,0 6,5 | |||
| Итого |
Рассчитайте для двух предприятий:
1) среднюю себестоимость единицы продукции;
2) индекс средней себестоимости продукции;
3) среднее изменение себестоимости продукции;
4) индекс структурных сдвигов.
Решение:
1) 
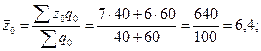
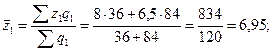
2) 
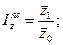
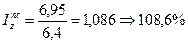
т.е. средняя себестоимость единицы продукции по двум предприятиям возросла на 8,6%;
3) 
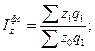
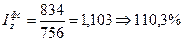
т.е. в среднем по двум предприятиям себестоимость повысилась на 10,3%;
4) 
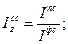
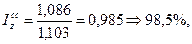
Задача 1.
По данным о динамике наличных денег в обращении во втором полугодии 2010 года рассчитайте показатели абсолютных приростов, темпов роста и прироста цепным и базисным методами. Определите абсолютное значение 1% прироста (A%).
| Показатель | 01.07 | 01.08 | 01.09 | 01.10 | 01.11 | 01.12 |
| M0, млрд. руб. | 3 522,5 | 3 550,1 | 3 506,6 | 3 485,6 | 3 566,7 | 3 600,1 |
Решение:
Динамика наличных денег в обращении
во втором полугодии 2010 года
| Показатель | 01.07 | 01.08 | 01.09 | 01.10 | 01.11 | 01.12 |
| M, млрд. руб. | 3 522,5 | 3 550,1 | 3 506,6 | 3 485,6 | 3 566,7 | 3 600,1 |
| Dyц, млрд. руб. | – | 27,6 | -43,5 | -21,0 | 81,1 | 33,4 |
| Dyб, млрд. руб. | – | 27,6 | -15,9 | -36,9 | 44,2 | 77,6 |
| Трц, % | – | 100,8 | 98,8 | 99,4 | 102,3 | 100,9 |
| Трб, % | – | 100,8 | 99,6 | 99,0 | 101,3 | 102,2 |
| Тпцi, % | – | 0,7835 | -1,2253 | -0,5989 | 2,3264 | 0,9364 |
| Тпбi, % | – | 0,7835 | -0,4514 | -1,0476 | 1,2548 | 2,2030 |
| А1%, млрд. руб. | – | 35,225 | 35,501 | 35,066 | 34,856 | 35,667 |
Задача 2.По данным таблицы определить среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект за полугодие:
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь |
| Средний размер выплаченного страхового возмещения, тыс. руб. |
Решение:
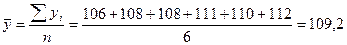(тыс.руб.)
Задача 3.По приведенным в таблице данным о размере денежных средств на счете вкладчика на начало каждого месяца определить средний размер вклада в I квартале:
| Дата | 01.01 | 01.02 | 01.03 | 01.04 |
| Остаток денежных средств, руб. | 132 000 | 147 289 | 151 870 | 148 500 |
Решение:
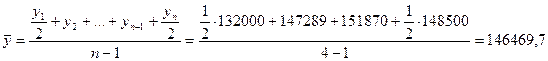(руб.)
Задача 4.По данным таблицы определить показатели абсолютных приростов размера страхового возмещения, выплаченного страховой компанией.
| Месяц | Средний размер выплаченного страхового возмещения, тыс. руб. | Абсолютные приросты | |
цепные 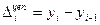 | базисные  | ||
| Январь Февраль Март Апрель Май Июнь | - -1 | - | |
| Итого | - | - |
Решение:
(тыс. руб.)
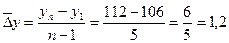(тыс. руб.)
Задача 5. Темпы роста объема долгосрочных кредитов, выданных банком, составили
(в % к предыдущему месяцу):
| Месяц | Февраль | Март | Апрель | Май |
| Темп роста, % | 100.3 | 96.8 | 104.2 | 102.5 |
Определите среднемесячный темп роста.
Решение:
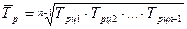
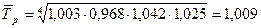
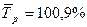
Задача 6.Темпы прироста прибыли, полученной банком (в % к 2008) составили:
2009 - +4
2010 - +10
2011 - +15
2012 - +31.1.
Определите среднегодовой темп прироста.
Решение:
1) 
2) 
, 
, 
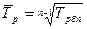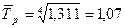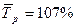
3) 
, 
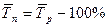Задача 7.
В таблице приведены отдельные показатели, характеризующие взаимосвязь показателей динамики по кредитной организации.
| Год | Прибыль, млн.руб. | Базисные показатели | ||
| Абсолютный прирост, млн.руб. | Темп роста, % | Темп прироста, % | ||
| 185,0 | - | 100,0 | - | |
| 2,3 | ||||
| 103,5 | ||||
| 5,8 | ||||
| 108,1 | ||||
| Всего | Х | Х | Х |
Рассчитайте:
1) недостающие в таблице показатели;
2) средний уровень ряда динамики;
3) средний абсолютный прирост;
4) средний темп роста и прироста.
Решение:
| Год | Прибыль, млн.руб. | Базисные показатели | ||
| Абсолютный прирост, млн.руб. | Темп роста, % | Темп прироста, % | ||
| 185,0 | - | 100,0 | - | |
| 187,3 | 2,3 | 101,2 | 1,2 | |
| 191,5 | 6,5 | 103,5 | 3,5 | |
| 195,7 | 10,7 | 105,8 | 5,8 | |
| 200,0 | 15,0 | 108,1 | 8,1 | |
| Всего | 959,5 | Х | Х | Х |
Для расчёта недостающих показателей в таблице используем формулы:
; 
; 
; 
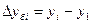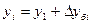
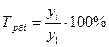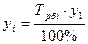
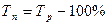Среднегодовой объём прибыли:
; 
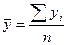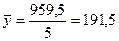млн.руб.
Среднегодовой абсолютный прирост прибыли:
; 
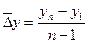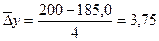млн.руб.
Среднегодовой темп роста прибыли:
; 
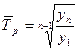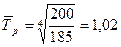(102%)
Среднегодовой темп прироста прибыли:
; 
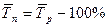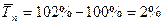
Задача 7
По данным результатов торгов на единой торговой сессии по доллару США за 2010 год определите тенденцию объёма торгов, используя метод укрупнения интервалов.
| Месяц | Объём торгов, млн. дол. США | Месяц | Объём торгов, млн. дол. США |
| Январь | 28 086 | Июль | 23 880 |
| Февраль | 23 903 | Август | 22 866 |
| Март | 20 846 | Сентябрь | 21 260 |
| Апрель | 19 572 | Октябрь | 19 029 |
| Май | 14 924 | Ноябрь | 18 175 |
| Июнь | 18 930 | Декабрь | 23 850 |
Решение:
Исходные (месячные) данные об объёме торгов объединяем в квартальные:
| I квартал: | 28086 + 23903 + 20846 = 72835 (млн. дол.США) |
| II квартал: | 19572 + 14924 + 18930 = 53426 (млн. дол.США) |
| III квартал: | 23880 + 22866 + 21260 = 68006 (млн. дол.США) |
| IV квартал: | 19029 + 18175 + 23850 = 61054 (млн. дол.США) |
Задача 8
По данным о среднемесячном курсе продажи доллара США за I полугодие 2010 года выполните выравнивание ряда, используя скользящую среднюю по трём месяцам.
| Показатель | Январь | Февраль | Март | Апрель | Май | Июнь |
| Курс продажи, руб./дол. | 32,2135 | 34,5578 | 34,8316 | 33,4507 | 32,0797 | 31,7226 |
Решение:
| Исходные данные | Расчетные данные | ||
| месяц | Продажа руб./долл. | Скользящая сумма трех членов | Скользящая средняя по трем членам(расчетные уровни ряда), |
| Январь | 32,2135 | – | – |
| Февраль | 34,5578 | 32,2135+34,5578+ +34,8316=101,6029 |  |
| Март | 34,8316 | 34,5578+34,8316 + + 33,4507=102,8401 |  |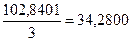
| Апрель | 33,4507 | 34,8316+33,4507+ +32,0797 =100,362 |  |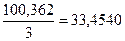
| Май | 32,0797 | 33,4507+32,0797 + +31,7226 = 97,253 |  |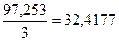
| Июнь | 31,7226 | 32,0797 + 31,7226+ +32,0470 =95,8493 |  |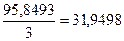
Задача 9. Имеются данные о доходах банка от операций с ценными бумагами:
| Год | ||||||
| Доход банков от операций с ценными бумагами, млн.руб. | ||||||
| Цепные абсолютные приросты | - |
Составить уравнение тренда, полагая, что выравнивание осуществляется с помощью линейной функции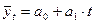 
.
Решение:
Цепные абсолютные приросты относительно постоянны, поэтому целесообразно выбрать в качестве аналитической функции уравнение прямой.
При нахождении параметров уравнения показатель времени удобно обозначать так, чтобы выполнялось следующее равенство: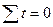 
.
Для этого при четном количестве уровней ряда (за период с 2007 по 2012 г.) в середине ряда находятся два периода времени. Одному присваивается значение t = -1, а другому t = +1. Тогда предыдущие периоды времени получают значения -3, -5 и т. д., а последующие значения - +3, +5 и т. д.
Определяем параметры уравнения прямой. Решаем систему нормальных уравнений:
Составим расчетную таблицу.
| Год | Доход банков от операций с ценными бумагами, млн.руб., y | t |  | y∙t |
| -5 -3 -1 | -350 -276 -112 | |||
| Сумма |
;
, 
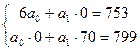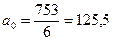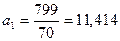
Искомое уравнение прямой имеет вид: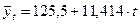 
Задача №1
В сберегательных банках города методом случайной повторной выборки отобрано 1600 счетов вкладчиков. Средний размер остатков вклада по этим счетам составил 3,2 тыс. руб. при коэффициенте вариации 30%.
Определите среднюю ошибку выборки.
Решение
1) из формулы для расчета коэффициента вариации находим среднее квадратическое отклонение
; 
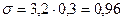(тыс.руб.)
2) находим среднюю ошибку повторной выборки:
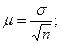
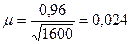(тыс.руб.) = 24 руб.
Величина средней стандартной ошибки выборочной доли определяется по формуле:
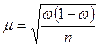
Средняя стандартная ошибка бесповторной выборки определяется по формулам:
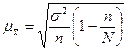и 
Применение бесповторного отбора взамен повторного приводит к уменьшению стандартной ошибки выборки.
Задача №2
При обследовании 200 образцов изделий, отобранных из партии в случайном порядке, оказалось 40 нестандартных.
Определите с вероятностью 0,954 среднюю ошибку доли нестандартной продукции.
Решение
1) находим долю нестандартных деталей в выборке
; 
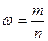или 20%
2) находим ошибку выборки
; 
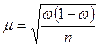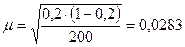или 2,83%.
Задача №3
На заводе электроламп из партии продукции в количестве 18 000 шт. ламп взято при случайном бесповторном отборе 1800 шт., из которых 40 шт. оказались бракованными. Определите стандартную ошибку выборки.
Решение
1) находим долю бракованных ламп в выборке
; 
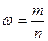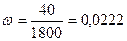или 2,22%
2) находим среднюю ошибку бесповторной выборки
; 
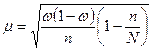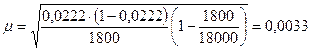или 0,33%
Задача №4
Методом случайной повторной выборки проверено 500 корреспондентских счетов в РКЦ Банка России на начало года. На основе полученных данных исчислен средний остаток денежных средств на счетах, равный 4 тыс. руб., и среднее квадратическое отклонение – 600 руб. С вероятностью 0,954 (коэффициент доверия равен 2) требуется определить пределы, в которых находится средний остаток денежных средств в генеральной совокупности.
Решение
1) находим среднюю ошибку повторной выборки
; 
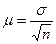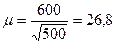(руб.)
2) находим предельную ошибку выборки
; 
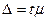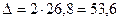(руб.)
3) находим доверительный интервал
; 
;
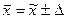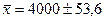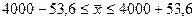
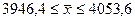
Задача №5
При проведении выборочного обследования своевременных расчетов по кредитам в КБ было взято (при повторном отборе) 500 кредитных договоров. Причем, в 10 случаях условия договора оказались невыполненными. Требуется с вероятностью 0,9545 (коэффициент доверия равен 2) определить, в каких пределах заключается доля несвоевременно погашенных кредитов по коммерческому банку.
Решение
1) находим долю невыполненных кредитных договоров
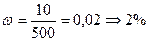
2) находим среднюю ошибку выборки
;
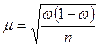3) находим предельную ошибку выборки
; 
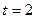
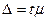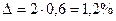
4) находим доверительный интервал
; 
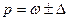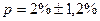
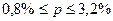
Вывод: в КБ доля невыполненных кредитных договоров с вероятностью 0,9545 находится в пределах от 0,8% до 3,2%.
Задача №6
В ходе аудиторской проверки из 2236 документов бухгалтерской отчетности банка, составляющих генеральную совокупность, по схеме случайной бесповторной выборки было отобрано 235 документов. Среди них обнаружено 14 документов, составленных с грубыми нарушениями.
1. Определите долю в выборке документов, составленных с грубыми нарушениями, и среднюю ошибку выборки.
2. Найдите, в каких пределах находится с вероятностью 0,683 доля документов бухгалтерской отчетности банка, составленных с грубыми нарушениями.
Решение
1) находим долю
; 
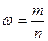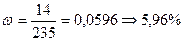
2) находим среднюю ошибку выборки
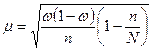
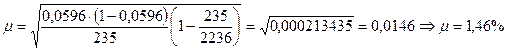
3) находим предельную ошибку выборки
; 
; 
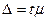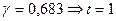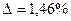
4) находим доверительный интервал
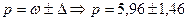
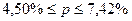
Вывод: в бухгалтерской отчетности банка доля документов, составленных с грубыми нарушениями, с вероятностью 0,683 находится в пределах от 4,50% до 7,42%.
Задача №7
Число вкладчиков отделения СБ 10000 человек. Для определения среднего размера вклада необходима выборка лицевых счетов способом механического отбора. На основании имеющихся данных сделано предположение, что среднее квадратическое отклонение размера вкладов составляет 900 руб. Определить необходимую численность выборки при условии, что с вероятностью 0,954 (коэффициент доверия равен 2) ошибка выборки не превысит 100 руб.
Решение
Выборка бесповторная
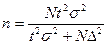
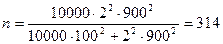чел.