Закон Био-Савара-Лапласа. Теорема Гаусса для магнитного поля
Магнитные свойства биообъектов.
Электромагнитные волны в биологических средах
(для иностранных студентов)
Подготовил: доцент, к.т.н. Руденко М.А.
План лекции:
Введение
Магнитное поле. Силовые линии магнитного поля. Вектор магнитной индукции
Закон Ампера.
Закон Био-Савара-Лапласа. Теорема Гаусса для магнитного поля.
Действие магнитного поля на движущийся заряд. Сила Лоренца.
Магнитное поле в веществе. Напряженность магнитного поля.
Явление электромагнитной индукции
Э.д.с. самоиндукции. Индуктивность. Энергия магнитного поля
Вихревое электрическое поле. Ток смещения
Уравнения Максвелла для электромагнитного поля
Магнитотерапия
Введение
Люди погружены в естественные и техногенные электромагнитные поля. Они не безразличны к этим полям так же, как и другие живые системы. Данный факт подтверждается огромным числом научных работ. Однако большинство авторов отмечает наличие проблемы: физическая причина явления до сих пор неизвестна и парадоксальна. Какие процессы лежат в основе взаимодействия магнитного поля с биологическими системами?
МАГНИТОБИОЛОГИЯ - раздел биофизики, изучающий влияние внешних магнитных полей на живые организмы, а также магнитные поля, создаваемые в организме (напр., в мозге, нерве и т. д.).
Магнитное поле. Силовые линии магнитного поля. Вектор магнитной индукции.
До знаменитых опытов Эрстеда, Био, Савара, Ампера и Фарадея (1819-1832), установивших связь магнитных явлений с электрическим током, под магнетизмом подразумевали совокупность явлений, связанных со свойствами природных магнитов (железорудных минералов) и земного магнитного поля, действие которого на магниты было обнаружено еще в древности и позволило создать компас. В теории, созданной Ампером, действие природных магнитов объяснено как действие кольцевых токов микроскопического масштаба, постоянно протекающих в толще магнитного материала. Современная наука, основываясь на квантовой теории, развитой в 20 веке, дополняет концепцию Ампера представлениями о собственном магнитном моменте частиц составляющих атомы и объясняет с единой точки зрения магнитные свойства не только природных магнитов, но и всех веществ.
В большинстве практических случаев магнитное поле – это поле, порождаемое электрическими токами (искусственными или природными) и действующее опять-таки на электрические токи. Это действие носит силовой характер.
Магнитное поле – это особый вид материи, посредством которого осуществляется связь и взаимодействие между движущимися электрическими зарядами. Существует в вещественной среде и в вакууме, обладает свойством неограниченности.
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности `Е электрического поля. Такой характеристикой является вектор магнитной индукции `В. Вектор магнитной индукции `В определяет силы, действующие на токи или движущиеся заряды в магнитном поле.
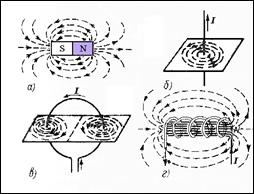За положительное направление вектора `В принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор`Внаправлен по касательной. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми (рис.10.1.1).
Закон Ампера.
Для того, чтобы количественно описать магнитное поле, нужно указать способ определения не только направления вектора `В,но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δl, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:
F ~ IΔl sin α. (10.2.1)
Эта сила называется силой Ампера. Она достигает максимального по модулю значения Fmax, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора `Вопределяется следующим образом:
Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δl:
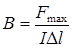
(10.2.2)
В общем случае сила Ампера выражается соотношением: F = IBΔl sin α.
Это соотношение принято называть законом Ампера.
В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).
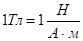
Закон Био-Савара-Лапласа. Теорема Гаусса для магнитного поля
Био и Савар (1820-1822) установили, что при удалении точки наблюдения от оси длинного прямолинейного провода, величина 
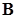изменяется обратно пропорционально расстоянию, к тому же она оказывается прямо пропорциональна току. Во всех случаях, когда магнитное поле создается током I, текущим вдоль тонкого провода (в том числе криволинейного), магнитная индукция 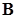может быть вычислена как суперпозиция элементарных векторов d 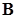, созданных каждым элементарным участком провода с током. Для d 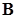Лапласом была получена формула, называемая законом Био-Савара-Лапласа:
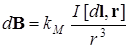, (10.3.1)
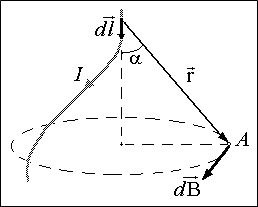
где dl- длина элементарного (бесконечно малого) участка провода,r– расстояние от этого участка до точки наблюдения. Вектор dl направлен вдоль направления протекания тока, вектор r – от данного элемента тока к точке наблюдения A (см. рис. 10.3.1). Коэффициент kM зависит от выбора системы единиц. В СИ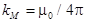 
, где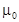 
= 
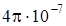Генри/метр – постоянная величина, которую называют магнитная постоянная.
Магнитное поле произвольных токовых систем можно найти с помощью закона Био-Савара-Лапласа и принципа суперпозиции:
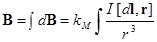(10.3.2)
где интегрирование необходимо проводить по всем элементам провода dl.
Замкнутость силовых линий указывает на то, что выполняется следующая теорема Гаусса для магнитного поля. Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
Поток 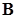определяется точно так же, как поток напряженности электрического поля. А именно, элементарный поток dФм магнитной индукции через площадку dS определяется как произведение нормальной компоненты 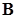в центре площадки на dS :
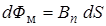. (10.3.3)
Поток магнитной индукции 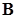(магнитный поток) через некоторую поверхность S определяется как сумма элементарных потоковчерез все бесконечно малые площадки dS этой поверхности:
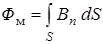. (10.3.4)
Пользуясь введенными обозначениями теореме Гаусса для магнитного поля в интегральной форме можно придать следующий вид
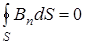(10.3.5)
Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2: 1 Вб = 1 Тл · 1 м2.