Методика расчета усилия и момента прокатки
В общем случае усилие прокатки F определяют по уравнению
F = pcp A, (6.1)
где рср - среднее контактное давление и А - площадь контакта металла с валками, значения которых вычисляются по формулам
рср = sS nx ns , А = bcp ld .
Таким образом, для вычисления усилия прокаткинеобходимо определить сопротивление деформации холодной или горячей полосы, площадь контакта металла с валком и среднее удельное давление, а затем по формуле (6.1) вычислить усилие прокатки.
Сопротивление металла деформации при холодной прокатке тонких полос может определяться по формуле Зюзина-Третьякова:
sS = s0 + a e b, (6.2)
где s0, a, b - экспериментально определяемые коэффициенты, которые характеризуют марку или группу марок сталей и сплавов (табл. 6.1); e - относительное обжатие полосы, %.
Таблица 6.1.
Коэффициенты для определения сопротивления деформации sS некоторых марок стали и сплавов при холодной прокатке
| Марка стали или сплава | Коэффициенты формулы (6.2) | ||
| ss0 | a | b | |
| Стали | |||
| Ст2 | 29,99 | 0,62 | |
| 08кп | 225,4 | 33,91 | 0,6 |
| 367,5 | 30,97 | 0,64 | |
| 84,87 | 0,48 | ||
| 09Г2 | 313,6 | 57,82 | 0,46 |
| 0Х18Н10Т | 388,1 | 23,52 | 0,91 |
| 12Х18Н9Т | 401,8 | 23,52 | 0,91 |
| Сплавы на основе алюминия | |||
| АМГ1 | 12,74 | 0,59 | |
| Д16 | 39,2 | 0,31 | |
| Сплавы на основе меди | |||
| Л59 | 171,5 | 28,42 | 0,64 |
| Л68 | 117,6 | 35,28 | 0,62 |
| Л90 | 225,4 | 28,42 | 0,52 |
| БрБ2 | 30,38 | 0,75 |
При горячей прокатке полос сопротивление деформации зависит от трех факторов: температуры, относительного обжатия и скорости деформации. Поэтому формула для определения сопротивления деформации при горячей прокатке имеет следующий вид:
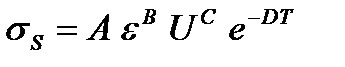 , (6.3)
, (6.3)
где A, B, C, D - коэффициенты, зависящие от марки стали (табл. 6.2); e - относительное обжатие; U - скорость деформации; Т - температура металла.
Таблица 6.2.
Коэффициенты для определения сопротивления деформации sS металла
При горячей прокатке
| Марка стали | Коэффициенты формулы (6.3) | |||
| A | B | C | D | |
| 08кп | 0,252 | 0,143 | 0,0025 | |
| Ст3 | 0,252 | 0,143 | 0,0025 | |
| 0,28 | 0,143 | 0,0025 | ||
| 09Г2С | 0,28 | 0,143 | 0,0025 | |
| 1Х17 | 0,26 | 0,117 | 0,0030 | |
| 40Х13 | 0,28 | 0,087 | 0,0033 | |
| Х18Н9Т | 0,278 | 0,092 | 0,0031 | |
| 12Х18Н10Т | 0,28 | 0,087 | 0,0028 |
Кроме того, для определения сопротивления деформации целого ряда сталей и сплавов можно использовать регрессионные уравнения. В качестве примера в табл. 6.3 приведены уравнения, отвечающие условиям прокатки на толстолистовых станах: e = 0,02…0,20; U = 1…25 c-1; Т = 850…1200 0С. Данные, полученные с помощью этих уравнений, позволяют рассчитать истинный предел текучести, зависящий не только от каждого в отдельности трех основных параметров прокатки, но и от их совместного влияния.
При расчете среднего контактного давления необходимо учитывать тот факт, что в случае плоской деформации (прокатка на листовых станах, когда уширение практически отсутствует) nx » 1,15. В том случае, когда деформация происходит в направлении всех трех главных осей (прокатка на блюмингах и слябингах), nx » 1.
Таблица 6.3.
Уравнения связи сопротивления деформации sS с термомеханическими параметрами при горячей прокатке
| Марка стали или сплава | Уравнения регрессии |
| 15Х12ВМФ | 1283+ 467e + 0,9 U - 1,85T – 1338 e2 + 0,00066 T2 + 5,3 e U |
| Х21Н14Г3Т | 758 + 1349 e + 1,2 U – 1,12 T – 903 e2 + 0,00043 T2 – 0,81e T |
| 12ХН3МДА | 464+2151 e - 3U - 0,414 T – 2953 e2 – 0,0734U2- 1,213e T+ 0,00632 UT |
| 4Х5В4Ф2М | 336 + 1097 e + 3,9U – 0,25 T – 0,74 e T – 0,0029 U T |
| 10ГН2МФА | 1804 + 627 e + 4,6 U – 2,9 T – 1343,8 e2 – 0,1 U2 + 0,00118 T2 |
| 48ТС-3-40 | 3517 – 261 e - 1,4 U – 6,5 T + 1630,6 e2 + 0,076 U2 + 0,00304 T2 |
При прокатке блюмов, слябов, заготовок и толстых листов, а также тонких полос при малых степенях деформации (горячая прокатка), когда фактор формы 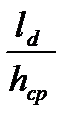 < 1, т. е. при коротком очаге деформации, существенное влияние на величину среднего контактного давления оказывают внеконтактные, в том числе глубинные зоны очага деформации, не охваченные пластической деформацией. Поэтому коэффициент напряженного состояния ns определяется по следующим соотношениям:
< 1, т. е. при коротком очаге деформации, существенное влияние на величину среднего контактного давления оказывают внеконтактные, в том числе глубинные зоны очага деформации, не охваченные пластической деформацией. Поэтому коэффициент напряженного состояния ns определяется по следующим соотношениям:
при 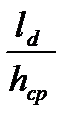 £ 0,6
£ 0,6 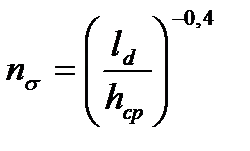 ;
;
при 0,6 < 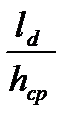 £1
£1 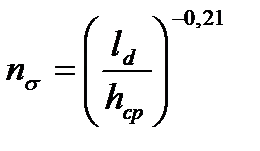 ,
,
при 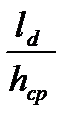 > 1
> 1 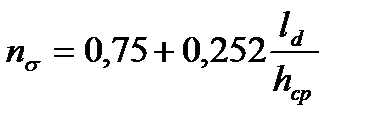 .
.
Если горячая прокатка полосы проводится с натяжением, когда фактор формы 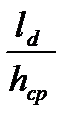 >1, то влияние натяжения концов полосы на контактное давление может быть учтено дополнительно с помощью формулы
>1, то влияние натяжения концов полосы на контактное давление может быть учтено дополнительно с помощью формулы
рср(нат) = рср 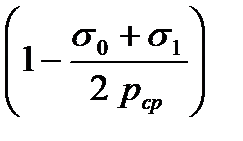
где s0 и s1 - заднее и переднее натяжение полосы; pcp - среднее контактное
давление без учета натяжения.
Если величины переднего и заднего натяжения совпадают, то
рср(нат) = рср 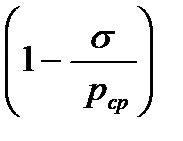
При холодной прокатке тонкой полосы для определения величины среднего удельного давления можно использовать формулу А.И. Целиковым:
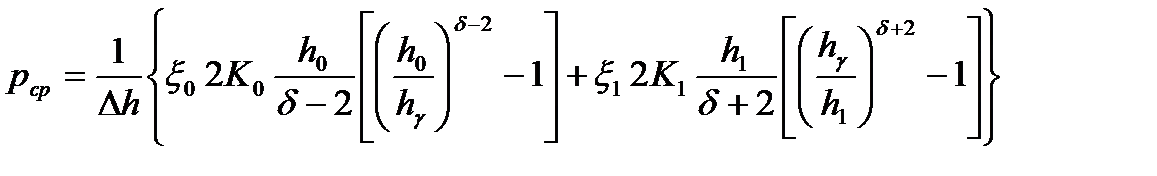 .
.
Значения hg , d, x0, x1 , 2К0 , 2К1 вычисляются следующим образом:
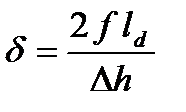 ;
; 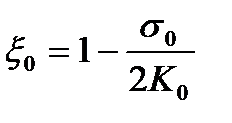 ;
; 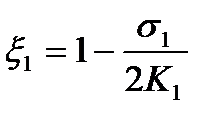 ,
,
где s0 и s1 - заднее и переднее натяжения; 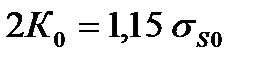 ;
;  - пределы текучести на входе в зону и выходе из зоны деформации при плоско- деформированном состоянии полосы; толщина полосы в нейтральном сечении
- пределы текучести на входе в зону и выходе из зоны деформации при плоско- деформированном состоянии полосы; толщина полосы в нейтральном сечении
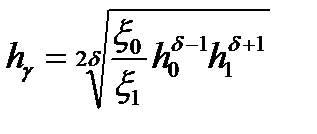 .
.
При расчете контактной поверхности следует иметь в виду, что под действием усилия прокатки валок несколько сплющивается и поэтому фактический радиус валка Rcпл будет больше начального радиуса R0 , т.е. Rcпл > R0. Тогда длину «сплющенной» дуги захвата определяют по формуле
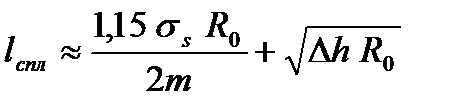 ,
,
где 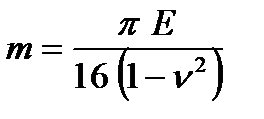 - модуль контактной жесткости валка; Е - модуль упругости материала валка; n - коэффициент Пуассона материала валка.
- модуль контактной жесткости валка; Е - модуль упругости материала валка; n - коэффициент Пуассона материала валка.
Величина т зависит только от механических свойств материала валков:
- для стальных валков Е = 2,06×105 МПа; n = 0,;
- для чугунных отбеленных валков Е = 1,26×105 МПа; n = 0,25.
При холодной тонколистовой прокатке, когда абсолютные обжатия меньше 1 мм, а отношение усилия прокатки на единицу ширины полосы 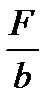 > 8000 Н/мм, учет сплющивания валков обязателен.
> 8000 Н/мм, учет сплющивания валков обязателен.
Момент прокатки Мпр определяется для правильного выбора двигателя и параметров оборудования клети. Существует несколько методов определения момента прокатки. Однако наибольшее распространение получили формулы, в которых крутящий момент определяют по усилию прокатки.
Мпр = F аF ,
где аF - плечо равнодействующей сил на контактной поверхности, т.е. силы F, относительно линии центров валков.
Плечо аF принято определять в долях длины очага деформации, т.е.
аF = y lд .
Величину y называют коэффициентом плеча момента прокатки.
Таким образом, для двух рабочих валков имеем
 . (6.4)
. (6.4)
Если считать, что усилие прокатки F = рср lд b (или контактное давление рср) задано, то основная проблема расчета крутящего момента сводится к правильному определению точки приложения силы F, т.е. к нахождению коэффициента плеча момента прокатки y . При практических расчетах для определения y используют эмпирические зависимости.
Наиболее известными зависимостями такого вида являются уравнения, которые получили В. М. Луговской для условий прокатки толстой полосы
y = 0,68 + 0,0018 e - 0,31 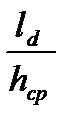 при
при 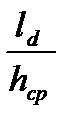 ≤ 1,
≤ 1,
и М. И. Бояршинов для условий прокатки тонких полос
y = 0,4566 – 0,021 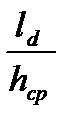 при
при 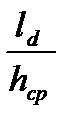 > 1,
> 1,
где e - относительное обжатие, %.
При наличии заднего F0 или переднего F1 усилия натяжения (или подпора) равнодействующая всех сил в очаге деформации отклоняется от вертикального направления; соответственно изменяется её плечо относительно центра валка. Положение равнодействующей в каждом конкретном случае можно определить из
условия равновесия всех продольных сил, приложенных к полосе. Тогда величина
крутящего момента может быть найдена по следующим зависимостям:
- при прокатке с задним натяжением – Мпр = 2F y ld + F0 R.;
- при прокатке с передним натяжением – Мпр =2 F y ld - F1 R.
Если силы натяжения приложены к обоим концам полосы – переднему и заднему, то формула крутящего момента принимает вид
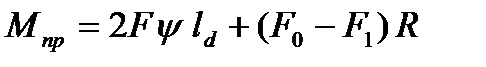 . (6.5)
. (6.5)
В частном случае, когда F0 = F1, т.е. равнодействующая F направлена вертикально и формула (6.5) совпадает с формулой крутящего момента (6.4) для свободной прокатки. Однако под воздействием сил F0 и F1 снижается величина равнодействующей F , а, следовательно, уменьшается крутящий момент.
На рис. 6.1. и 6.2. представлены блок-схемы алгоритма расчета усилия и крутящего момента применительно к условиям прокатки на станах горячей и холодной прокатки.
| ∆h ,ε, ld, U |
| hср, ld/hср |
| ∆h<3 мм |
| nσ, pср |
| σs |
нет
| Учет натяжения |
да
| ld(спл)/hср, Rспл, U, σs |
| nσ, pср(спл) |
да нет
| Учет натяжения |
| F, M |
| pср(нат) |
| Fспл, Mспл |
| Fнат, Mнат |
| Конец расчета |
Рис. 6.1. Блок-схема расчета усилия и момента при горячей прокатке с учетом «сплющивания» валков и натяжения полосы
Рис. 6.2. Блок-схема расчета усилия при холодной прокатке с учетом «сплющивания» валков и натяжения полосы
Примеры расчета
Пример 1. Построить кривые деформационного упрочнения стали Х21Н14Г3Т, полученные при скоростях деформации 5, 10, 15, и 20 с-1. Температура 850, 950, 1050, 11500С, обжатия 2, 5, 10, 15 и 20%.
Решение.
Определим сопротивление деформации 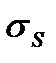 для каждого обжатия, температуры и скорости деформации, используя уравнение регрессии для стали Х21Н14Г3Т
для каждого обжатия, температуры и скорости деформации, используя уравнение регрессии для стали Х21Н14Г3Т
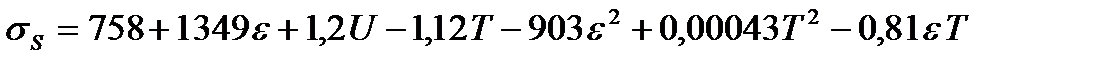
Возьмем Т = 850 °С, U = 5 с-1 и последовательно рассчитаем σS для ε = 0,02 , 0,05 , 0,1 и 0,2 :
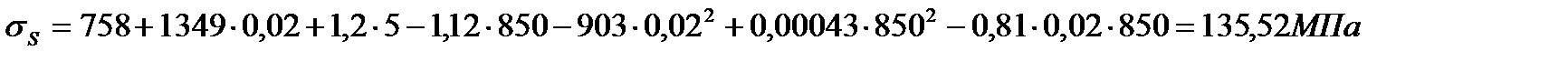
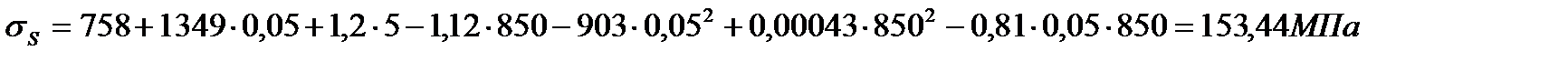
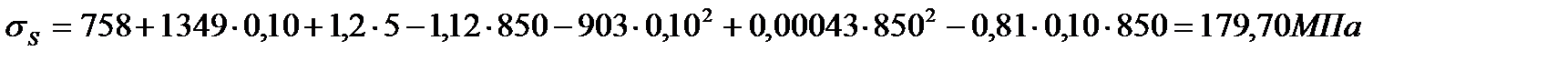
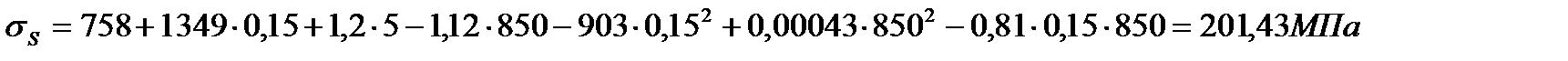
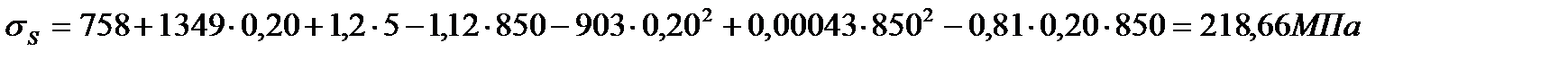
Расчет  для остальных значений обжатия, скорости деформации и температуры аналогичен. Полученные результаты заносим в табл. 6.4. и используем их для построения графиков зависимости σS от обжатия, скорости деформации и температуры (рис. 6.3).
для остальных значений обжатия, скорости деформации и температуры аналогичен. Полученные результаты заносим в табл. 6.4. и используем их для построения графиков зависимости σS от обжатия, скорости деформации и температуры (рис. 6.3).
Таблица 6.4. Зависимость сопротивления деформации sS стали Х21Н14Г3Т от скорости деформации, обжатия и температуры
| Скорость деформации, U, c-1 | Обжатие ε, % | Сопротивление деформации sS, МПа, при температуре Т, ºС | |||
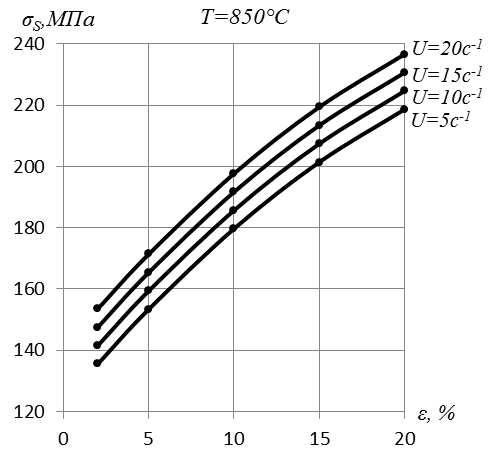
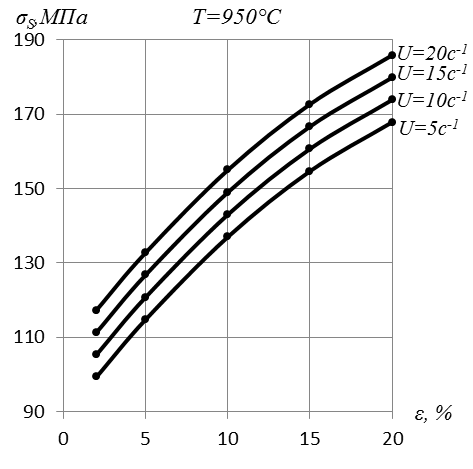
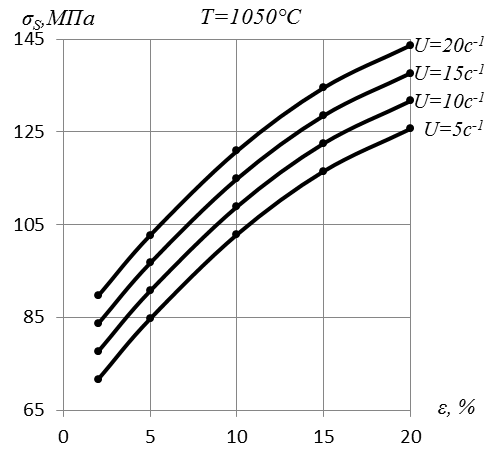
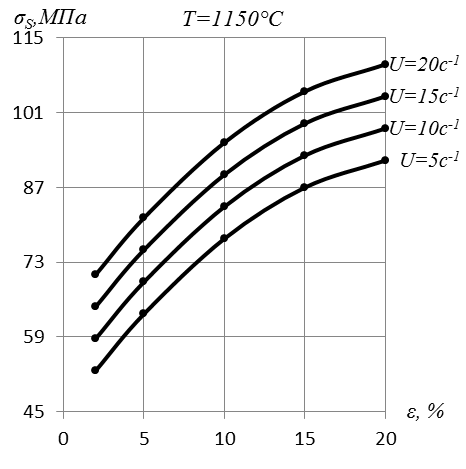
Рис. 6.3. Зависимость истинного предела текучести стали Х21Н14Г3Т от обжатия при разных температурах и скоростях деформации.
Пример 2.Определить сопротивление деформации полосы из стали 10ГН2МФА и стали 45 при прокатке в реверсивной клети стана 4500 если известно, что толщина полосы h0 = 24 мм, h1 = 20 мм. Прокатка велась на стальных валках диаметром 1030 мм при температуре 980 0С. Окружная скорость валков 60 об/мин.
Решение.
1. Определяем абсолютное и относительное обжатие
Dh = h0 – h1 = 24 – 20 = 4 мм; e = 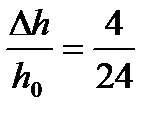 =0,167.
=0,167.
2. Вычисляем длину дуги захвата
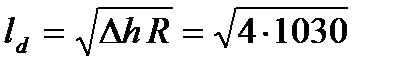 = 64,19 мм.
= 64,19 мм.
3. Вычисляем скорость прокатки, исходя из окружной скорости валков
v = 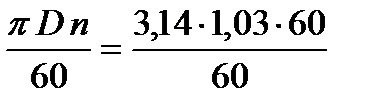 = 3,23 м/с.
= 3,23 м/с.
4. Находим среднее значение скорости деформации полосы
U = 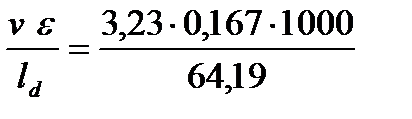 = 8,40 с-1.
= 8,40 с-1.
5. Определяем сопротивление деформации полосы из стали 10ГН2МФА по регрессионной зависимости (табл. 6.3)
ss = 1804 + 627 e + 4,6 U – 2,9 T – 1343,8 e2 – 0,1 U2 + 0,00118 T2 =
=1804 + 627× 0,167 + 4,6× 8,4 – 2,9× 980 – 1343,8× 0,1672 – 0,1× 8,42 + 0,00118× 9802 =
= 194,09 МПа.
6. Находим сопротивление деформации полосы полосы из стали 45 по формуле (6.3), используя данные табл. 6.2.
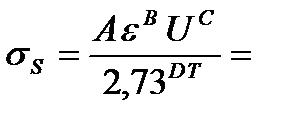
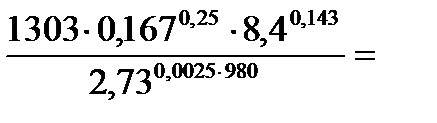 97,7 МПа.
97,7 МПа.
Пример 3.На НШС холодной прокатки прокатали полосу из стали 08Х18Н10Т толщиной 0,6 мм. Диаметр валков в последней клети 480 мм, окружная скорость 797 об/мин, истинное сопротивление деформации при прокатке 564 МПа. Определить среднюю скорость деформации в последней клети стана.
Решение.
1. Сопротивление деформации при холодной прокатке вычисляется по формуле
ss = s0 + a eb.
Используя данные табл. 6.1. находим коэффициенты уравнения для этой марки стали и определяем относительное обжатие в последней клети стана
 e =
e = 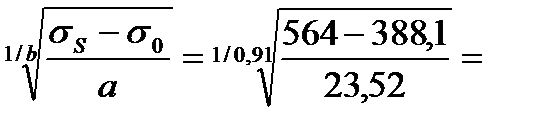 9,13% = 0,091.
9,13% = 0,091.
2. Находим толщину полосы на входе в клеть
h0 = 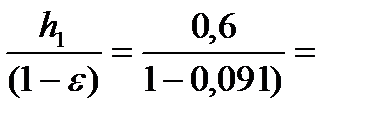 0,66 мм.
0,66 мм.
3. Вычисляем абсолютное обжатие в последней клети
Dh = h0 –h1 = 0,66 – 0,6 = 0,06 мм.
4. Определяем длину дуги захвата металла валками в последней клети
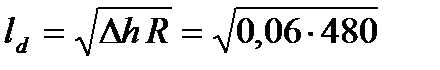 = 5,37 мм.
= 5,37 мм.
5. Вычисляем скорость прокатки в последней клети
v =  = 20,02 м/с.
= 20,02 м/с.
6. Определяем скорость деформации полосы в последней клети
U = 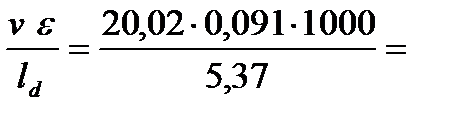 339 c-1.
339 c-1.
Пример 4.На толстолистовом стане 3000 прокатали полосу из стали 40Х13 толщиной h1 = 49 мм с обжатием в последнем проходе 11 мм. Сопротивление деформации, при этом, составляло 172 МПа. Определить скорость прокатки, если известно, что температура прокатки Т = 880оС, а диаметр чугунных валков Dв = 900 мм.
Решение.
1. Вычисляем толщину полосы на входе в клеть
h0 = h1 + Dh = 49 + 11 = 60 мм.
2. Определяем относительное обжатие полосы
e = 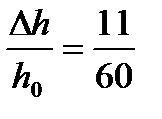 = 0,183.
= 0,183.
3. Вычисляем длину дуги захвата металла валками
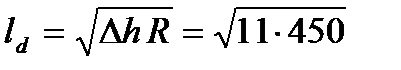 = 70,36 мм.
= 70,36 мм.
4. Находим скорость деформации металла по формуле (6.3), используя данные табл. 6.2
U = 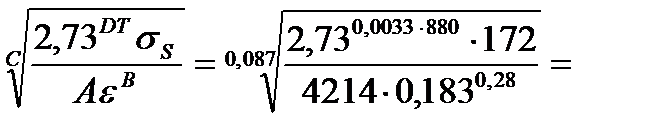 8,13 c-1
8,13 c-1
5. Вычисляем скорость прокатки, исходя из формулы определения скорости деформации
v = 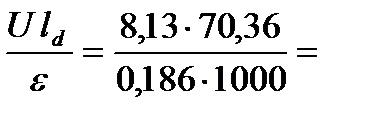 3,07 м/с.
3,07 м/с.
Пример 5.В реверсивной клети ТЛС с диаметром валков 870 мм в один из проходов был прокатан лист толщиной 22 мм и шириной 2400 мм. При этом, абсолютное обжатие составляло 4 мм, а момент прокатки Мпр = 1,04 МН×м. Определить сопротивление деформации прокатанного металла.
Решение.
1. Сопротивление деформации прокатанного металла можно рассчитать через связь усилия и момента прокатки:
Мпр = 2Р y ld = 2 pcp b ld y ld = 2×1,15 ns ss b y ld2 = 2×1,15 ns ss b y Dh R
Отсюда
ss = 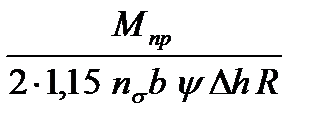
2. Определяем фактор формы очага деформации:
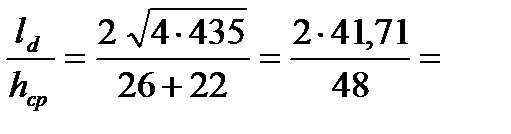 1,74;
1,74;
3. Вычисляем коэффициент напряженного состояния металла и коэффициент плеча момента по эмпирической зависимости М.И. Бояршинова. Так как 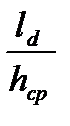 > 1,то
> 1,то
ns = 0,75 + 0,252 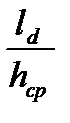 = 0,75 + 0,252×1,74 = 1,19;
= 0,75 + 0,252×1,74 = 1,19;
y = 0,4566 – 0,021 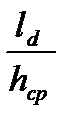 = 0,4566 – 0,021×1,74 = 0,42.
= 0,4566 – 0,021×1,74 = 0,42.
4. Определяем сопротивление деформации прокатанного металла:
ss =  = 216 МПа .
= 216 МПа .
Пример 6.В реверсивной клети ТЛС с диаметром валков 1000 мм в один из проходов прокатали лист шириной 3000 мм. При этом, контактное давление
рср = 120 МПа, а момент прокатки 2,16 МНм (y = 0,6).Определить абсолютное обжатие за проход и коэффициент трения, обеспечивающий свободный захват металла валками.
Решение.
1. В уравнение, определяющее момент прокатки Мпр = 2 F y ld = 1,2 F ld , подставим значение усилия прокатки F = рср b ld .Тогда
Мпр = 1,2 рср b ld ld = 1,2 рср b Dh R .
2. Определяем абсолютное обжатие за проход
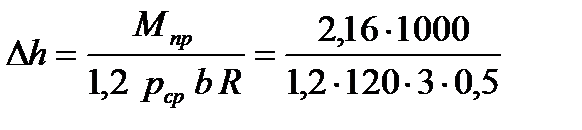 = 10 мм.
= 10 мм.
3. Находим угол захвата полосы валками для этого обжатия
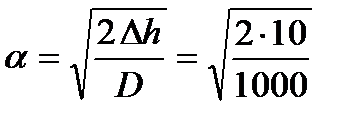 = 0,447 рад.
= 0,447 рад.
Таким образом, чтобы произошел свободный захват полосы валками коэффициент трения должен быть f ≥ 0,447.
Пример 7. Слиток из стали 12Х18Н10Т прокатывают на слябинге 1150 в стальных валках со скоростью 1,24 м/с при температуре 11800С. Размеры поперечного сечения слитка при прокатке в одном из проходов, мм: h0 = 650, h1 = 570, b0 = 710, b1 = 720. Определить усилие и момент, действующие на валки при прокатке.
Решение.
1. Определяем абсолютное и относительное обжатие
Dh = h0 – h1 = 650 –570 = 80 мм;
e = 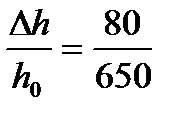 = 0,123 = 12,3%.
= 0,123 = 12,3%.
2. Проверяем условия захвата металла валками
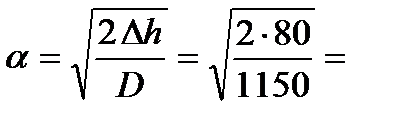 0,373 рад.
0,373 рад.
f = 1,05 – 0,0005 Т – 0,056 v = 1,05 – 0,0005 × 1180 – 0,056 × 1,24 = 0,391.
Захват возможен, так как .α = 0,373 < f = 0,391.
3. Вычисляем длину дуги захвата
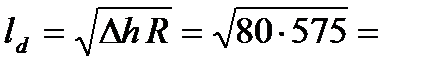 214 мм .
214 мм .
4. Вычисляем среднюю скорость деформации полосы
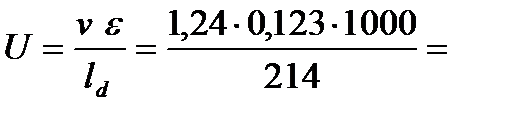 0,71 с-1 .
0,71 с-1 .
5. Вычисляем истинный предел текучести полосы
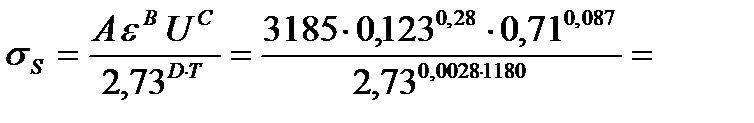 63,02 МПа .
63,02 МПа .
6. Определяем показатель фактора формы очага деформации
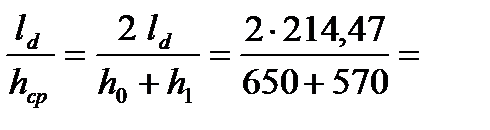 0,35.
0,35.
7. Определяем коэффициент напряженного состояния. Так как 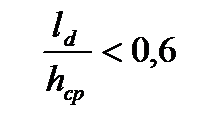 то
то
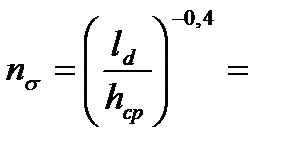 0,35 -0,4 =1,52.
0,35 -0,4 =1,52.
8. Вычисляем среднее контактное давление металла на валки. Так как имеем объёмную схему деформации (В0 ≠ В1), тоnx = 1
рср = nx ns sS = 1× 1,52 × 63,02 = 95,79 МПа .
9. Определяем контактную площадь:
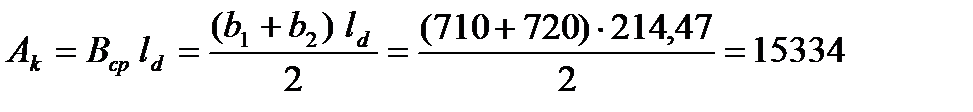 мм2 = 0,153 м2 .
мм2 = 0,153 м2 .
10. Определяем усилие прокатки
F= pcp Ak = 95,79 × 0,153 = 14,66 MH .
11. Вычисляем момент прокатки, используя формулу В.М. Луговского для нахождения коэффициента плеча равнодействующей
y = 0,68 + 0,0018 e - 0,31 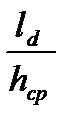 = 0,68 + 0,0018∙12,3 – 0,31∙0,35 = 0,59;
= 0,68 + 0,0018∙12,3 – 0,31∙0,35 = 0,59;
Мпр = 2 F y ld = 2 × 14,66 × 0,59 × 214,47 × 10-3 = 3,71 МНм .
Пример 8.Определить усилие и момент, действующие на валки при горячей прокатке листа из стали 4Х5В4Ф2М в чистовой клети ТЛС 5000. Частота вращения валков 58 об/мин, температура прокатки 10500С, толщина подката 92 мм, ширина 3820 мм, обжатие в клети 12 мм. Рабочие валки стальные и имеют диаметр 1150 мм.
Решение.
1. Находим относительное обжатие и толщину листа после прохода
ε = 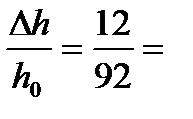 0,130 = 13%;
0,130 = 13%;
h1 = h0 – Dh = 92 – 12 = 80 мм.
2. Вычисляем длину дуги захвата
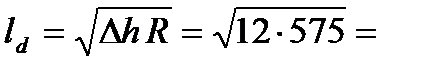 83,07 мм .
83,07 мм .
3. Вычисляем скорость прокатки полосы
v = 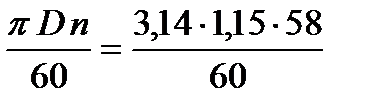 = 3,49 м/с.
= 3,49 м/с.
4. Находим среднюю скорость деформации металла
U = 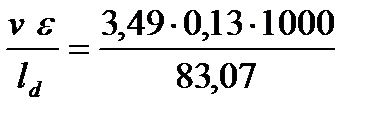 = 5,46 c-1.
= 5,46 c-1.
5. Находим истинное сопротивление деформации металла, используя регрессионную зависимость для этой марки стали из табл. 6.3
ss = 336 + 1097e + 3,9U – 0,25T – 0,74eT – 0,0029UT = 336+1097× 0,13+
+ 3,9× 5,46 – 0,25×1050 – 0,74× 0,13×1050 –0,0029× 5,46×1050 = 119,77 МПа.
6. Определяем показатель фактора формы очага деформации
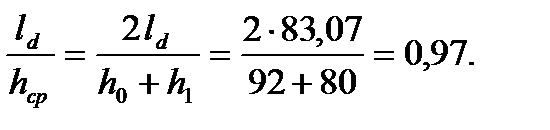
7. Определяем коэффициент напряженного состояния
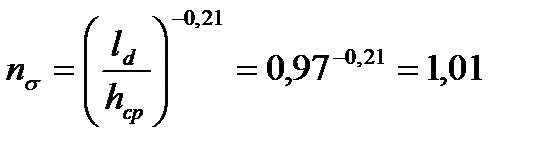 .
.
8. Вычисляем среднее контактное давление металла на валки. Так как имеем плоскую схему деформации, тоnx = 1,15.
рср = nb ns sS = 1,15 × 1,01 × 119,77 = 139,11 МПа .
9.. Определяем усилие прокатки
F= pcp B l d = 139,11× 3820× 83,07×10-6= 44,14 MH .
10. Вычисляем момент прокатки, используя формулу В.М. Луговского для нахождения коэффициента плеча равнодействующей
y = 0,68 + 0,0018 e - 0,31 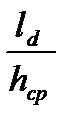 = 0,68 + 0,0018∙13 – 0,31∙0,97 = 0,40.
= 0,68 + 0,0018∙13 – 0,31∙0,97 = 0,40.
Мпр = 2 F y ld = 2×44,14×0,4×83,07×10-3 = 2,93 МН·м .
Пример 9.Определить усилие и момент, действующие на валки при горячей прокатке полосы из стали 45 в последней клети чистовой группы НШС 2000. Скорость прокатки 17,6 м/с, температура прокатки 8600С, толщина подката 4 мм, на выходе из клети лист имеет толщину 3,4 мм, ширина полосы 1520 мм. Заднее натяжение отсутствует, переднее 27 МПа. Рабочие валки чугунные диаметром 800 мм.
Решение.
1. Определяем абсолютное и относительное обжатие в последней клети
Dh = h0 – h1 = 4 – 3,4 = 0,6 мм; e = 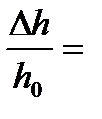
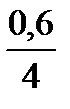 = 0,15.
= 0,15.
2. Вычисляем длину дуги захвата
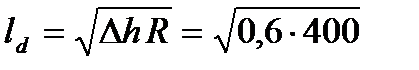 = 15,49 мм.
= 15,49 мм.
3. Находим скорость деформации металла
U =  = 170,41 c-1.
= 170,41 c-1.
4. Рассчитываем сопротивление металла деформации по формуле (6.3), используя данные табл. 6.2 для стали 45
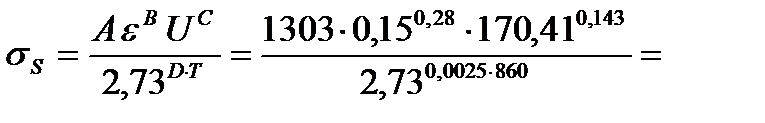 185,79 МПа.
185,79 МПа.
Так как Dh = 0,6 мм, тонеобходимо пересчитывать длину дуги захвата с учетом «сплющивания» валков.
5. Определяем модуль контактной жесткости валка и заново рассчитываем длину дуги захвата
m = 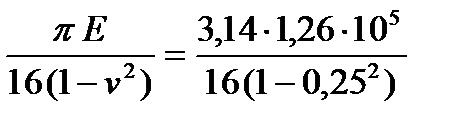 = 26376 МПа;
= 26376 МПа;
ld(спл) =  =17,12 мм
=17,12 мм
Тогда Rспл. =  = 488,5 мм.
= 488,5 мм.
6. Пересчитываем среднюю скорость деформации полосы и истинный предел текучести
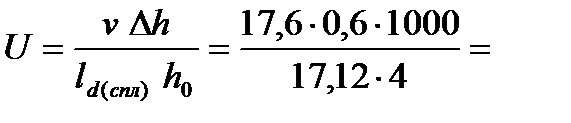 154,21 c-1.
154,21 c-1.
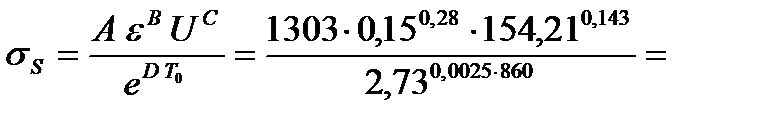 183,16 МПа.
183,16 МПа.
7. Определяем показатель формы очага деформации
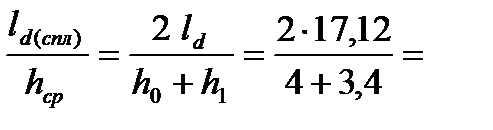 4,63.
4,63.
8. Определяем коэффициент напряженного состояния. Так как 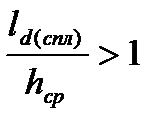 , то
, то
ns = 0,75 + 0,252 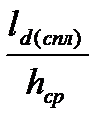 = 0,75 + 0,252 × 4,63 = 1,92.
= 0,75 + 0,252 × 4,63 = 1,92.
9. Вычисляем среднее контактное давление металла на валки
рср = 1,15 ns sS = 1,15 × 1,92 × 183,16 = 404,42 МПа.
10. Находим усилие и момент прокатки
F = pcp b ld(спл) = 404,42 × 1520 × 17,12 × 10-6 = 10,52 МН,
y = 0,4566 – 0,021 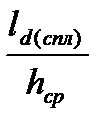 = 0,4566 – 0,021∙4,63 = 0,36 ,
= 0,4566 – 0,021∙4,63 = 0,36 ,
Мпр = 2 F y ld(спл) = 2 × 10,52 × 0,36 × 17,12 × 10-3 = 0,130 МН·м.
15. Учитываем влияние натяжения концов полосы на контактное давление
рср(нат) = рср  = 390,92 МПа.
= 390,92 МПа.
16. Определяем усилие прокатки с учетом натяжения полосы
Fнат = рср(нат) b ld(спл) = 390,92 × 1520 ×17,12× 10-6 = 10,17 МН .
17. Определяем момент прокатки с учетом натяжения
Мпр(нат) = Мпр – F1 Rспл = 0,130 - 27∙3,4∙1520∙488,5∙10-9= 0,0618 МНм.
Пример 10. Определить усилие и момент, действующие на валки при горячей прокатке полосы 15,8х1560 мм из стали Ст3 во второй клети чистовой группы НШС 2500. Скорость прокатки 5,44 м/с, температура полосы 10100С, относительное обжатие в клети 34,2%. Заднее натяжение 10 МПа, переднее – 20 МПа. Рабочие валки из отбеленного чугуна имеют диаметр 800 мм.
Решение.
1. Определяем абсолютное обжатие и толщину полосы на выходе из второй клети
D h = e h0 = 0,342× 15,8 = 5,4 мм,
h1 = h0 - ∆h = 15,8 – 5,4 = 10,4 мм.
2. Вычисляем длину дуги захвата и среднюю толщину полосы
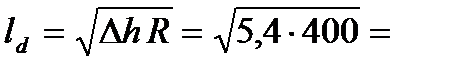 46,48 мм ,
46,48 мм ,
hср = 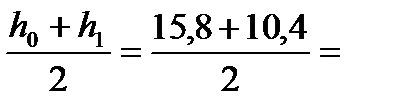 13,1 мм.
13,1 мм.
3. Находим среднюю скорость деформации металла
U = 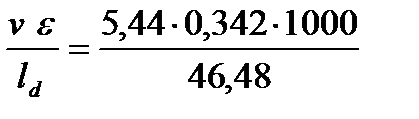 = 40,03 c-1.
= 40,03 c-1.
4. Вычисляем истинный предел текучести полосы, используя данные для этой марки стали из табл. 6. 2.
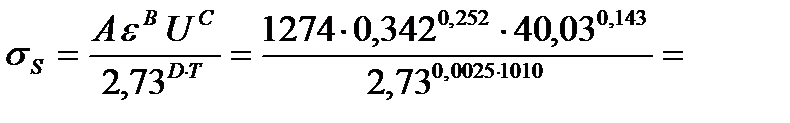 130,80 МПа .
130,80 МПа .
5. Определяем показатель фактора формы очага деформации
 = 3,55.
= 3,55.
6. Определяем коэффициент напряженного состояния полосы.Так как схема деформации плоская, то уширение не учитывается и коэффициент nx = 1,15. Тогда
ns = 0,75 + 0,252  = 0,75 + 0,252×3,55 = 1,64.
= 0,75 + 0,252×3,55 = 1,64.
7. Рассчитываем среднее контактное давление
рср = nx ns ss = 1,15 × 1,64× 130,80 = 246,69 МПа.
8. Находим усилие и момент для случая свободной прокатки
F = pcp b ld = 246,69 × 1560 × 46,48 × 10-6 = 17,89 МН,
y = 0,4566 – 0,021 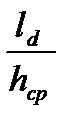 = 0,4566 – 0,021∙3,55 = 0,38 ,
= 0,4566 – 0,021∙3,55 = 0,38 ,
Мпр = 2 F y ld = 2 × 17,89 × 0,38 × 46,48 × 10-3 = 0,632 МН·м.
9. Учитываем влияние на контактное давление натяжение полосы с помощью формулы
рср(нат) = 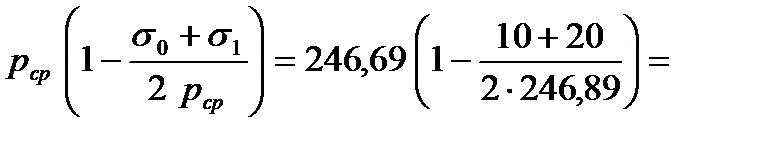 231,89 МПа.
231,89 МПа.
10. Определяем усилие прокатки:
Fнат = pcp B ld = 231,89×1560× 46,48×10-6= 16,81 MH .
11. Корректируем момент прокатки с учетом натяжения полосы
Мпр(нат) = Мпр + 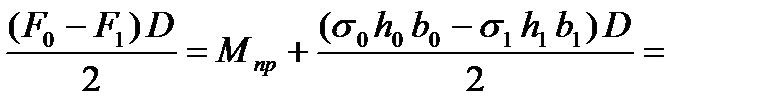
= 0,632 + 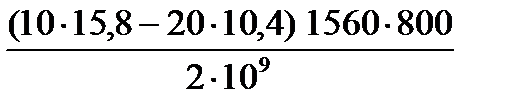 = 0,60 МНм.
= 0,60 МНм.
Пример 11. Определить усилие, действующее на валки при прокатке полосы стали 12Х18Н9Т в первой клети чистовой группы НШС 1700 холодной прокатки. Скорость прокатки 7,88 м/с, толщина полосы на выходе из клети 1,45 мм, ширина полосы 1250 мм, обжатие 0,55 мм. Заднее и переднее натяжение равны соответственно 20 и 60 МПа. Прокатка ведется на сухих стальных шлифованных валках диаметром 500 мм.
Решение.
1. Определяем толщину полосы на входе в клеть
h0 = h1 + Dh = 1,45 + 0,55 = 2,0 мм.
2. Находим относительное обжатие полосы
e = 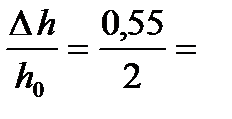 0,275 = 27,5%
0,275 = 27,5%
3. Определяем по формуле (6.2) с учетом данных табл. 6.1 истинный предел текучести полосы после прокатки
sS1 = sS0 + a eb = 401,8 + 23,52×27,50,91 = 881 МПа .
4. Вычисляем длину дуги захвата без учета «сплющивания» валков
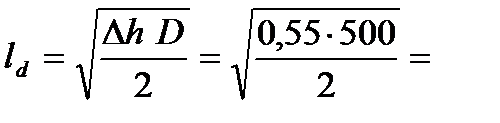 11,73 мм.
11,73 мм.
5. Определяем коэффициенты заднего x0 и переднего x1 натяжения
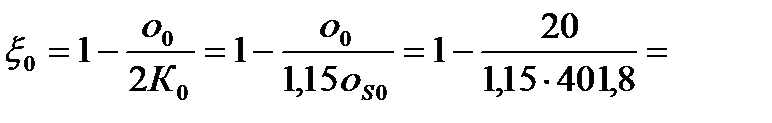 0,9567;
0,9567;
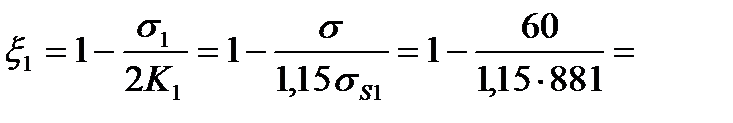 0,9408.
0,9408.
6. Вычисляем коэффициент контактного трения при холодной прокатке. Так как валки сухие, то Км = 1,55:
f = Kм 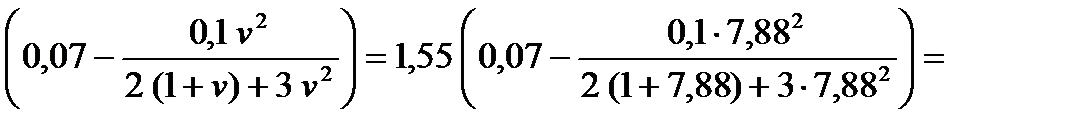 0,06.
0,06.
7. Вычисляем коэффициент d
 2,56.
2,56.
8. Определяем толщину полосы в нейтральном сечении
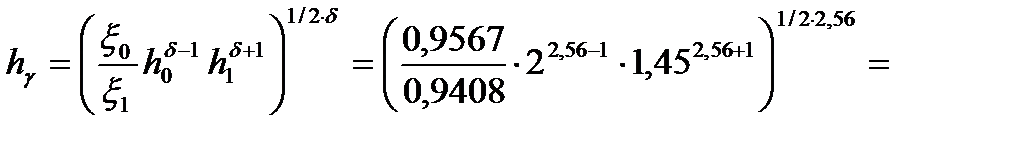 1,60 мм .
1,60 мм .
9. Вычисляем среднее контактное давление при прокатке
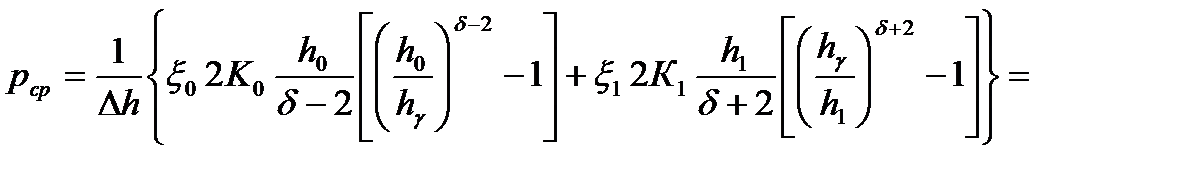
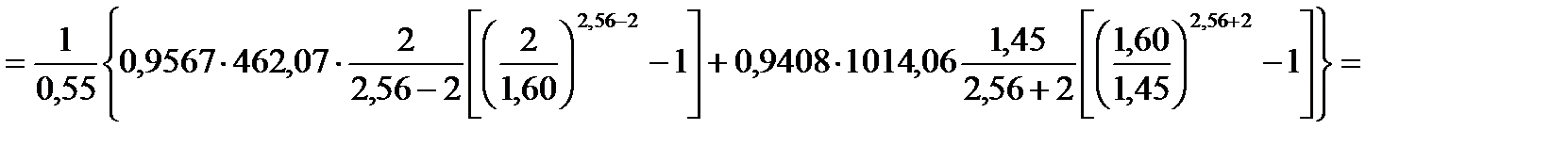 = 700,45 МПа .
= 700,45 МПа .
10. Определяем усилие прокатки
F = pcp ld b = 700,45 × 11,73× 1250 × 10-6 = 10,27 МН .
11. Проверяем отношение усилия прокатки на единицу ширины полосы
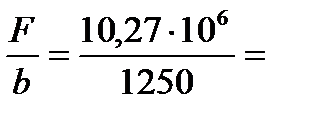 8216 Н·м.
8216 Н·м.
Так как полученная величина больше 8000 Н·м, «cплющивание» валков необходимо учитывать.
12. Определяем модуль контактной жесткости стальных валков
m = 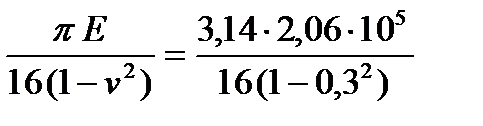 = 44425 МПа;
= 44425 МПа;
ld(спл) = 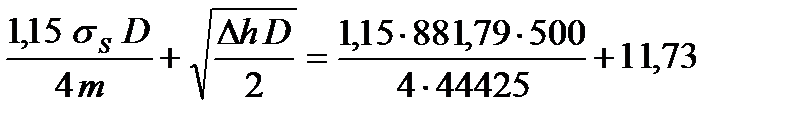 =14,56 мм.
=14,56 мм.
13. Уточняем значение коэффициента d
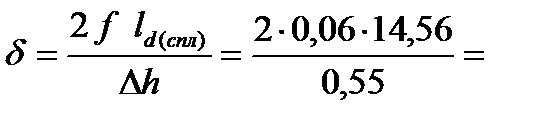 3,18.
3,18.
14. Находим толщину полосы в нейтральном сечении с учетом «сплющивания» валков
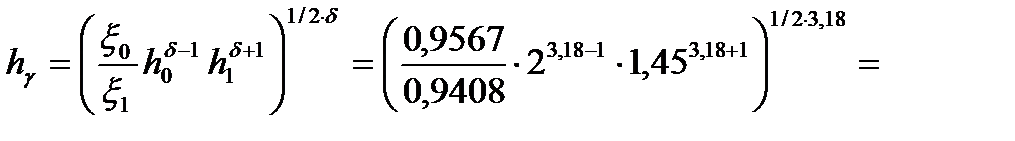 1,62 мм.
1,62 мм.
15. Пересчитываем среднее контактное давление
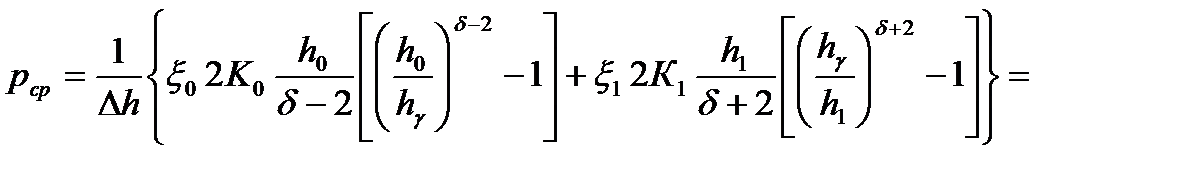
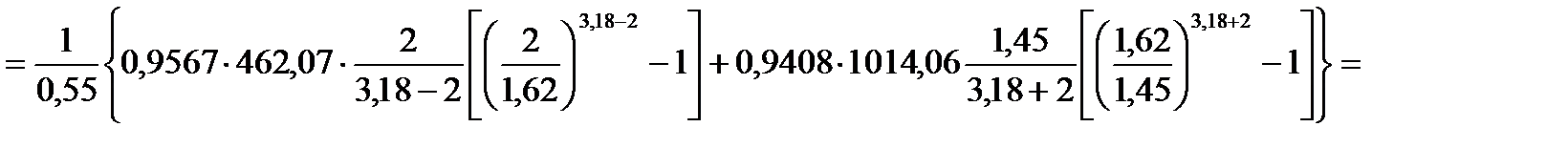
= 766,24 МПа.
16. Определяем усилие прокатки с учетом «сплющивания» валков
Fспл. = pcp ld b = 766,24 × 14,58× 1250 × 10-6 = 13,96 МН .
Пример 12.Определить усилие, действующее на валки при прокатке полосы из стали 09Г2 во второй клети НШС 2500 холодной прокатки. Диаметр стальных валков 490 мм, скорость прокатки 10,8 м/с, толщина полосы на выходе из первой клети 2,13 мм, ширина 1700 мм, относительное обжатие 15,2%. Прокатка ведется со смазкой валков (10% эмульсия) и натяжением: заднее – 10 МПа, переднее - 25 МПа.
Решение.
1. Определяем абсолютное обжатие полосы во второй клети
Dh = e h0 = 0,152 × 2,13 = 0,34 мм.
2. Вычисляем толщину полосы на выходе из второй клети
h1 = h0 – Dh = 2,13 – 0,34 = 1,79 мм.
3. Вычисляем длину дуги захвата без учета «сплющивания» валков
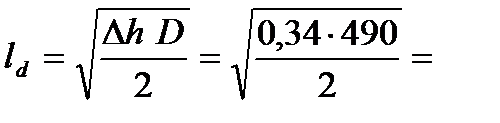 9,13 мм.
9,13 мм.
4. Определяем истинный предел текучести полосы после прокатки
sS1 = sS0 + a eb = 313,6 + 57,82 × 15,20,46 = 515 МПа .
5. Определяем коэффициенты заднего x0 и переднего x1 натяжения
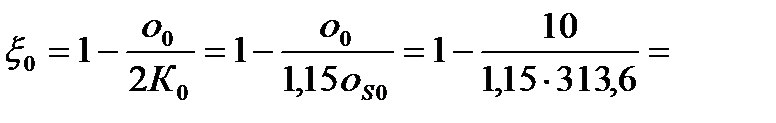 0,8675;
0,8675;
 0,8741.
0,8741.
6. Вычисляем коэффициент контактного трения при холодной прокатке с использованием смазки валков
f = Kм 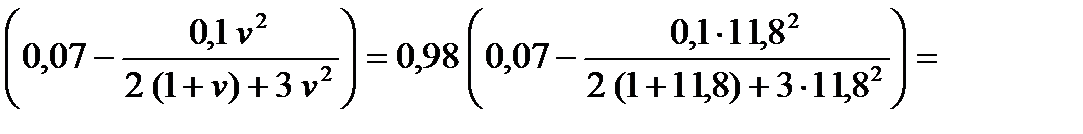 0,04
0,04
7. Вычисляем коэффициент d
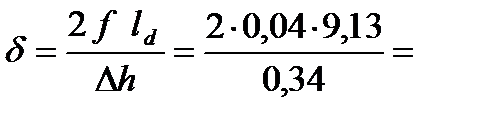 2,15.
2,15.
8. Определяем высоту полосы в нейтральном сечении
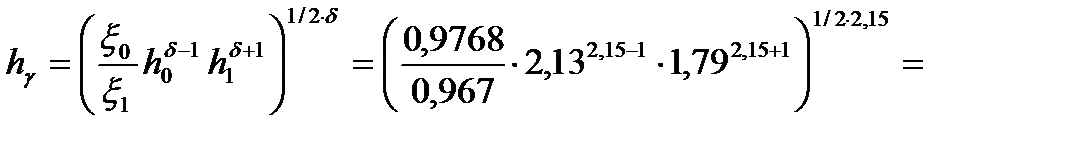 1,87 мм .
1,87 мм .
9. Вычисляем среднее контактное давление при прокатке
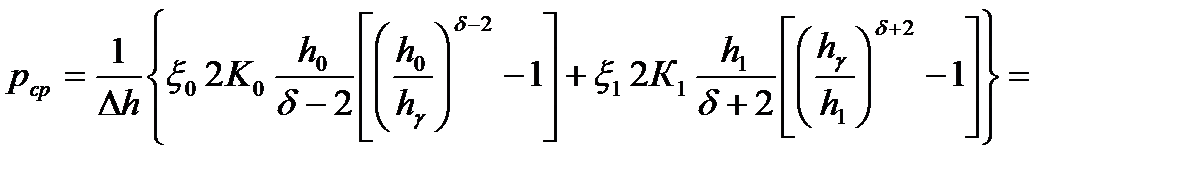
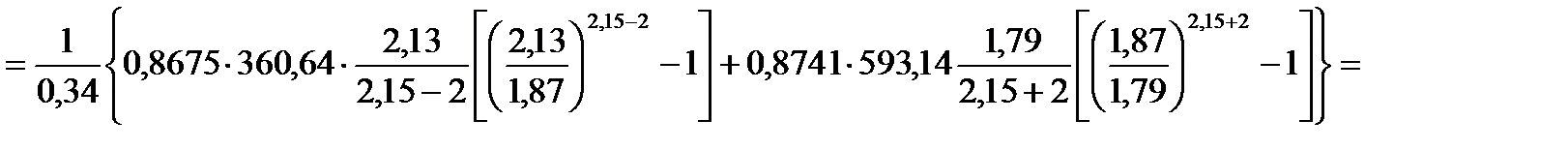
= 389,74 МПа .
10. Определяем усилие прокатки
F = pcp ld b = 389,74 × 9,13× 1700 × 10-6 = 6,05 МН .
11. Проверяем отношение усилия прокатки на единицу ширины полосы
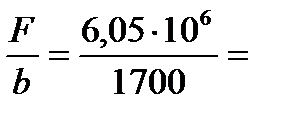 3559 Н/мм.
3559 Н/мм.
