Проектировочный расчет

По табл. 3.2 [1] принимаем для колеса предел контактной выносливости

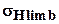= 2НВ + 70 = 2×245 + 70 = 560 МПа.

Срок службы привода в часах

t_ч = t_год ∙ 300 ∙ t_смен ∙ 7 = 8 ∙ 300 ∙ 2 ∙ 7 = 33600 ч;

число циклов нагружений зубьев колеса.

N_НЕ = 60 t_час ∙ n₂ = 60 ∙ 33600 462 = 9,314∙10⁸.

Базовое число циклов для материала колеса (по табл.3.2 [1])

.

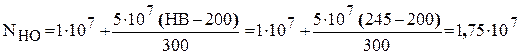Коэффициент долговечности

.

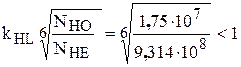Следовательно, при длительной эксплуатации коэффициент долговечности К_HL = 1. Примем коэффициент безопасности [S_Н] = 1,15.

Допускаемые контактные напряжения

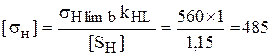МПа.

Коэффициент К_Нв при консольном расположении шестерни равен 1,35 (табл. 3.1 [1]). Коэффициент ширины венца по отношению к внешнему конусному расстоянию y_bRe= 0,285 (рекомендация ГОСТ 12289-76).

Внешний делительный диаметр колеса (по формуле (3.29) [1])

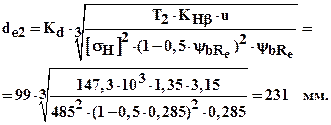
Для прямозубых передач К_d = 99,

u= u_p= 3,15.

Принимаем по ГОСТ 12289-76 ближайшее стандартное значение d_e2 = 250 мм. [1, с. 49].

Число зубьев шестерни выбираем из интервала 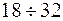.Число зубьев шестерни примем z₁=25; число зубьев колеса

z₂ = z₁^.u = 25^.3,15 = 78,75.

Примем z₂ = 79. Тогда

u = z₂/ z₁ = 79/25 = 3,16.

Отклонение от заданного (3,16 - 3,15)/3,15^.100 % = 0,32 %, что меньше установленных ГОСТ 2185-66 допустимых 3 %.

Внешний окружной модуль [1, с. 50]

m_e = d_e2/z₂ = 250/79 ≈ 3,164 мм.

Примем m_e = 3,2 ,

d_e2 = m_e ^. z₂ =3,2^.79 = 253 мм.

Отклонение от стандартного (253 - 250)/250^.100 % = 1,1 %, что меньше допустимых 2 %.

Внешний делительный диаметр шестерни

d_е1 = m_еz₁ = 3,2×25 = 80 мм.

Углы делительных конусов (по табл. 3.11):

ctg d₁ = u = 3,16;

d₁ =17°34’;

d₂ = 90° - d₁ = 90° - 17°34’ = 72°26’.

Внешнее конусное расстояние R_е и длина зуба b:

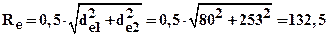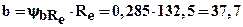мм;

мм.

Принимаем b = 38 мм.

Внешние диаметры шестерни и колеса (по вершинам зубьев):

d_ае1 = d_е1 + 2m_е^.cos d₁ = 80 + 2×3,2×cos 17°34’ = 86,1 мм;

d_ае2 = d_е2 + 2m_е^.cos d₂ = 253 + 2×3,2×cos 70°26’ = 255 мм.

Средний делительный диаметр шестерни

d₁ = 2^.(R_e - 0,5b)×sin d₁ = 2^.(132,5 - 0,5×38)×sin 17°34’ = 68,2 мм.

Средний окружной модуль

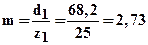мм.

Коэффициент ширины шестерни по среднему диаметру (по формуле (3.8) [1])

.

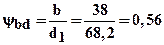Средняя окружная скорость колес

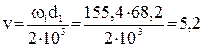м/с.

Примем 7-ю степень точности, т.к. для конических передач обычно принимают 7-ю степень точности.

Силы в зацеплении

Силы в зацеплении (по формулам (8.6) и (8.7) [1]):

окружная сила

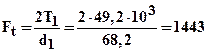Н;

радиальная для шестерни, равная осевой для колеса,

F_r1 = F_а2 = F_t tg a cos d₁ = 1443×tg 20°×cos 17°34’ = 501 Н;

осевая для шестерни, равная радиальной для колеса,

F_а1 = F_r2 = F_t tg a sin d₁ = 1443×tg 20°×sin 17°34’ = 158 Н.

Проверочный расчет на контактную выносливость

Для проверки контактных напряжений определяем коэффициент нагрузки:

.

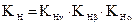По табл. 3.5 [1] при Ш_bd =0,56, при консольном расположении колес и твердости НВ<350 коэффициент, учитывающий распределение нагрузки по длине зуба, – К_Нb = 1,23.

Коэффициент, учитывающий распределение нагрузки между прямыми зубьями, – К_Нa= 1,02 (табл. 3.4 [1]).

Коэффициент, учитывающий динамическую нагрузку в зацеплении для прямозубых колес при 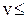5 м/с, – К_Нv=1,05 (табл. 3.6 [1], принято предельное значение).

Таким образом, К_Н = 1,23×1,02×1,05 = 1,3.

Проверяем контактное напряжение

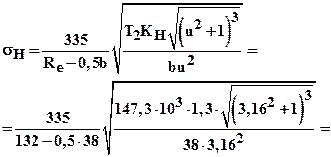
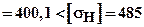МПа.

Проверочный расчет на контактную статическую прочность

При пиковой нагрузке

Расчетные контактные напряжения при пиковой нагрузке по формуле 3.21 [1]

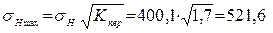МПа.

Допускаемое контактное напряжение при действии максимальной нагрузки для стальных колес с улучшением

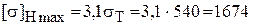МПа,

где предел текучести для стали Ст 40Х при диаметре заготовки > 160 мм s_т = 540 МПа;

s_Hmax = 521,6 < [s]_Hmax = 1674 МПа.

Условие прочности выполняется.