Проектировочный расчет передачи

Делительный диаметр шестерни

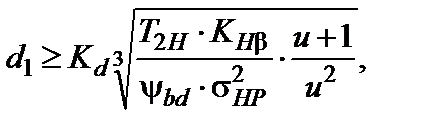
где K_d – вспомогательный коэффициент; K_d = 675 – для косозубых передач;

Ориентировочное значение межосевого расстояния [2,с. 45]

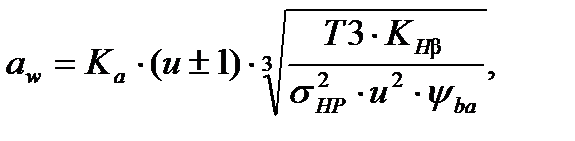
где знак «плюс» используется при расчете передач внешнего зацепления, а «минус» – для передач внутреннего зацепления;

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БНТУ 105081.018.ПЗ

K_a – вспомогательный коэффициент: [2, с.45];

Т₃ – вращающий момент на колесе (на ведомом звене);

u – передаточное число передачи;

К_Hβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, принимают в зависимости от твердости колес и параметра ψ_bd по графику [2, рис. 5.3]:

ψ_bd = b₂ / d₁ = 0,5 ψ_ba(u ± 1);

ψ_bd – коэффициент ширины колеса относительно делительного диаметра шестерни;

ψ_ba – коэффициент ширины колеса относительно межосевого расстояния; принимают из стандартного ряда чисел в зависимости от положения колес относительно опор [2, с. 22].

K_а = 430;

ψ_ba = 0,4; для косозубых

ψ_bd = 0,5 [0,4(4 + 1)] = 1;

K_Hβ = 1,12;

;

Полученное ориентировочное межосевое расстояние округляем до стандартного значения по предпочтительному ряду [2, табл. 5.4, с. 55]. Принимаем а_w = 135 мм.

Нормальный модуль при принятой термообработке колес рекомендуется выбирать из диапазона

m_n = (0,01–0,02) а_w = (0,01–0,02) · 135 = (1,35–2,7) мм.

Из стандартного ряда модулей [2, табл. 5.5, с. 55] принимаем m = 2 мм.

Рабочая ширина колеса:

b₂ = ψ_ba · а_w = 0,4 · 135 = 51 мм;

Ширина шестерни:

b₁ = b₂ + (2–7) мм = 51 + (2–7) = 53-58 мм.

Принимаем b₁ = 56 мм.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БНТУ 105081.018.ПЗ

Угол наклона зубьев β = 7–18°.

Предварительно приняв коэффициент осевого перекрытия εβ = 1 [8, с. 174, табл. 9.1], определим минимальный угол наклона зубьев:

sin β = π · mn εβ / b2 = 3,14 · 2 · 1 / 51 = 0,1256;

β = 7°12'55'' или βmin = arcsin(4mn / b2).

Величиной угла β можно задаться, например, β = 10°.

Суммарное число зубьев [2, с.46]

z_∑ = (2 · а_w · cos β) / m = (2 · 135 ·cos 7,2154) / 2 = 133,930.

Принимаем z_∑ = z₁ + z₂ = 124.

Определим числа зубьев шестерни z₁ и колеса z₂.

z₁ = z_∑ / (u +1) =124 / (4 +1) = 24,8;

принимаем z₁ = 25;

z₂ = z_∑ – z₁ = 124 – 25 = 99.

Фактическое передаточное число u_ф = z₂ / z₁ = 99/25 = 3,960.

∆u = (u_ф – u) / u · 100 % = ((4– 3,96) / 4) · 100 %) = 1% ≤ 4 %.

Уточним угол наклона зубьев:

cos β = m (z₁ + z₂)/(2 · а_w) = 2 (25 + 99) / (2 · 135) = 0,918;

β = 7,25220° =7°15’8’’

Определим делительные диаметры, диаметры вершин и впадин зубьев зубчатых колес:

d₁ = m · z₁ / cos β = 2 · 25 / 0,992 = 54,44 мм;

d₂ = m · z₂ / cos β = 2 · 99 / 0,992 = 215,56 мм;

d_а1= d₁ + 2 · m = 50,403 + 2 · 2 = 58,44 мм;

d_а2 = d₂ + 2 · m = 199,596 + 2 · 2 = 219,56мм;

d_f1= d₁ – 2,5 · m =50,403 – 2 · 2,5 = 57,15 мм;

d_f2 = d₂ – 2,5 · m = 199,596 – 2 · 2,5 = 210,56 мм.

Выполним проверку межосевого расстояния:

а_w = (d₁ + d₂) / 2 = (50,403 + 199,596) / 2 = 135 мм.

Вычислим величину усилий, действующих в зацеплении :

– окружная:

F_t = 2 · Т₃ / d₂ =2 · 314,871 / 199,596= 3155,08 Н;

– радиальная:

F_r = F_t · tg α_tw / cos β = 3155,08 ·tg 20° / 0,918 = 1157,61 Н;

– осевая:

F_а = F_t · tg β = 3155,08 ·tg7,25220° = 401,499 Н;

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БНТУ 105081.018.ПЗ .ПЗ

Проверочный расчет передачи на контактную усталость

Контактная выносливость устанавливается сопоставлением действующих в полюсе зацепления расчетного σ_Н и допускаемого σ_НР контактных напряжений [2, с.48]:

σ_Н = σ_Н0 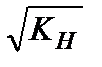≤ σ_НР,

где σ_Н0 – контактное напряжение в полюсе зацепления при K_Н = 1 [2, с.48]:

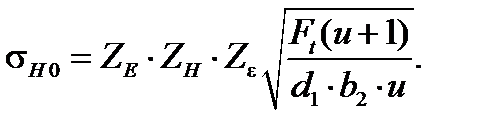
Коэффициент нагрузки K_Н определяют по зависимости [2, с.49]:

K_Н = K_А · K_Hv · K_Hβ · K_Hα,

где K_A = 1 – коэффициент, учитывающий внешнюю динамическую нагрузку [2,с.49];

K_Hv – коэффициент, учитывающий внутреннюю динамическую нагрузку, возникающую в зацеплении до зоны резонанса [2, с.49]:

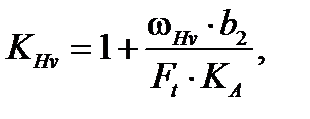
где ω_Hv – удельная окружная динамическая сила, Н/мм [2, с.49]:

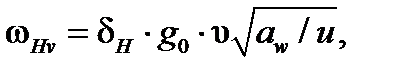
где δ_Н – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля головок зубьев [2,табл. 5.7];

g₀ – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса [2,табл. 5.8];

υ – окружная скорость зубчатых колес:

υ = πd_in_i/60;

K_Hα – коэффициент, учитывающий распределение нагрузки между зубьями [2,табл. 5.9];

ε_β – осевой коэффициент перекрытия: ε_β = b₂ · sin β / (π · m);

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БНТУ 105081.018.ПЗ БНТУ 303115.017.ПЗ

Z_E – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес; для стальных колес Z_E = 190 [2,с49];

Z_H – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления [2, с.49]:

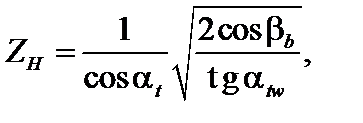
где α_t – делительный угол профиля в торцовом сечении: α_t = α = 20° [2, с.50];

β_b – основной угол наклона для косозубой передачи:

β_b = arcsin (sin β · cos 20°) ,[2, с.50];

α_tω – угол зацепления (без смещения);

tg α_tw = tg α / cos β [2, с.50];

Z_ε – коэффициент, учитывающий суммарную длину контактных линий (2, с.50); для косозубых передач при ε_β ≥ 1

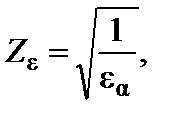
при εβ < 1

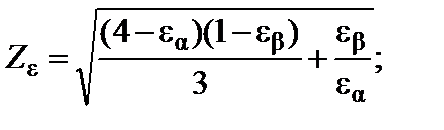
εα – коэффициент торцового перекрытия [8, с. 175, табл. 9.1]:

ε_α – коэффициент торцового перекрытия [2, с.50]:

ε_α = [1,88 – 3,2 (1 / z₁ ± 1 / z₂)] cos β.

Для рассчитываемого объекта имеем следующие данные: редуктор цилиндрический косозубый одноступенчатый,

частота вращения ведущего вала n₂ = 320,040мин^-1,

передаточное число редуктора u_ф =3,960;

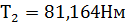
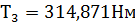
n₃ = 80

z₁=25;

z₂=99;

β = 7,25220° =7°15’8’’;

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БНТУ 105081.018.ПЗ

m=3мм;

a=135 мм;

b₂=51мм;

d₁=50,403 мм;

F_t = 3155,08 Н.

ε_β = b₂ · sinβ / (π · m) = 54 sin7,25220° / (3,14 ·2) = 1,085>1;

tg α_t = tgα / cosβ = tg20° / cos sin7,25220° = 0,3669;

α_t = 20,1484°;

β_b = arcsin (sinβ·cos20°) = 6,8127°;

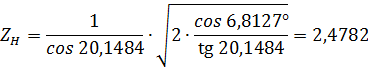
Z_E =190 МПа^1/2 ;

ε_α = [1,88 – 3,2 (1/25+ 1 / 99)] cos7°15’8’’ = 1,705;

;

;

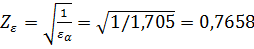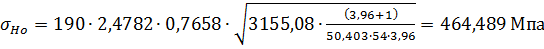υ = 3,14 · 50,403 · 320,040 / (60 ·10³) = 0,844 м/с.

Для данной скорости колес степень точности – 9-я [2, табл. 5.6].

δ_Н = 0,02; g₀ = 7,3;

;

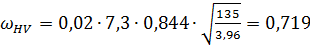K_Hv = 1+ (0,719 · 54)/3155,08= 1,012;

K_Hα = 1,0; K_А =1,0; K_Hβ = 1,12;

Изм.

Лист

№ докум.

Подпись

Дата

Лист

БНТУ 105081.018.ПЗ БНТУ 303115.017.ПЗ

K_Н = 1,0 · 1,012 · 1,12 · 1,0 = 1,133.

;

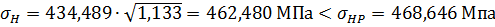Определим процент недогрузки:

∆σ_Н = |σ_НР – σ_Н| / σ_НР ·100 % = |468,646 –462,480| / 468,646 · 100 % = 1,3 %.

Условие прочности выполняется. По принятым в машиностроении нормам допускаются отклонения +5 % (перегрузка) и –10 % (недогрузка).