Этапы проведения корреляционного анализа

Многофакторный корреляционный анализ позволяет установить наличие, тесноту и форму связи между факторами и изучаемым показателем. Он состоит из нескольких этапов, деление на которые условно, так как отдельные стадии тесно связаны между собой.

Рассмотрим эти этапы.

1На первом этапе определяются цели и задачи исследования и на основе качественного анализа подбираются факторы, которые предположительно влияют на изучаемый показатель.

При их подборе необходимо учитывать:

– наличие причинно-следственных связей между показателями;

– значимость факторов, то есть степень их влияния на результативный показатель;

– возможность количественного измерения фактора.

2На втором этапе осуществляется сбор и первичная обработка исходной информации.

Совокупность данных должна быть достаточно большой. Информация должна соответствовать закону нормального распределения, согласно которому основная масса наблюдений по каждому показателю должна быть сгруппирована около его среднего значения.

Исходные данные должны быть качественно и количественно однородны. Качественная однородность предполагает приблизительно одинаковые условия и специфику формирования факторных и результативного признаков. Количественная однородность заключается в отсутствии таких наблюдений, которые значительно (аномально) отличаются от основной массы данных.

3 На третьем этапе осуществляется моделирование связей между факторами и результативным признаком, т.е. решается вопрос о выборе формы связи.

На основе экономического и логического анализа природы и сущности изучаемого явления подбирается тип математического уравнения, которое наилучшим образом отражает характер изучаемых зависимостей.

Обоснование уравнения связи проводится с помощью группировки данных, построения графика и т.д.

Размещение точек на графике показывает, какая зависимость образовалась: прямолинейная или криволинейная.

Для парной корреляции прямолинейную зависимость описывает уравнение прямой

у = a_o + a₁x_1,

а для множественной корреляции – уравнение линейной функции

у = а_о + а₁х₁ + а₂х₂ + … + а_nх_n,

где у – результативный показатель ;

а_о–постоянная величина, которая не связана с изменением факторов ;

аi - коэффициенты при переменных в уравнении регрессии;

хi - факторные показатели (переменные).

4На четвертом этапе проводится расчет численных значений параметров регрессионного уравнения. Он осуществляется методом наименьших квадратов, при котором в случае прямолинейной зависимости прямая на графике пройдет наиболее близко к точкам фактических наблюдений. Для этого решается система нормальных уравнений.

Построение уравнения регрессии проходит шаговым способом. При этом существуют два варианта:

а) сначала в расчет принимается один фактор, который является наиболее значимым, потом добавляется второй, третий и т.д. На каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции, коэффициент детерминации и статистические показатели, характеризующие надежность уравнения связи. Чем выше величины коэффициентов корреляции и лучше статистические характеристики, тем точнее уравнение связи описывает изучаемые зависимости. Если добавление новых факторов не улучшает оценочные показатели, то их надо отбросить и остановиться на том уравнении, где эти показатели наиболее оптимальны.

б) при втором варианте построение модели происходит в обратном порядке путем последовательного исключения наименее значимых факторов.

5. На пятом этапе дается статистическая оценка уравнения связи и экономическая интерпретация результатов корреляционного анализа.

Многофакторный корреляционный анализ играет важную роль в экономических исследованиях, так как позволяет:

1) изучить закономерности изменения результативного показателя в зависимости от разных факторов;

2) определить уровень внутрихозяйственных резервов;

3) спрогнозировать уровень изучаемого показателя.

Для определения резервов увеличения или снижения изучаемого экономического показателя за счет i-го фактора величина изменения этого фактора умножается на соответствующий ему коэффициент в уравнении регрессии (с его знаком).

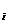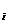∆у(х )=a ×∆x ,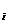

где а 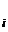-коэффициент в уравнении регрессии при i-м факторе;

Dx 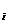-отклонение i-го фактора.

Тема 5