Интегральный метод измерения влияния факторов на результативный показатель.

Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток: при значительных отклонениях фактических данных от базисных результаты расчетов зависят от последовательности подстановок, в соответствии с которой замена осуществляется сначала по количественным и структурным факторам, затем – по качественным.

Однако, на практике встречаются модели, где все факторные показатели либо качественные, либо количественные, а иногда сложно определить какими они являются.

Кроме того, факторы действуют на результативный показатель не изолировано, а одновременно и взаимосвязано, что приводит к его дополнительному приросту (положительному или отрицательному), который при применении способов элиминирования присоединяется, как правило, к влиянию последнего фактора.

В связи с этим в детерминированном анализе может применяться интегральный метод для мультипликативных, кратных и смешанных моделей.

Его использование позволяет получать более точные результаты расчетов потому, что в данном случае они не зависят от порядка факторов в модели, а дополнительный прирост результативного показателя распределяется между ними.

Наиболее распространен интегральный метод для двухфакторных мультипликативных моделей.

Например, для двухфакторной модели вида.

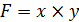
Влияние каждого фактора определяется по формулам:

.

∆F(y) = ∆y × x_o + (∆x ×∆y)/2.

Для трехфакторной модели вида

F= x × y × z

влияние каждого фактора определяется по формулам:

∆F(x) = 1/2∆x × (y_o × z₁ + y₁ × z_o) +1/3 × ∆x × ∆y × ∆z;

∆F(y) = 1/2∆y × (x_o × z₁ + x₁ × z_o) +1/3 × ∆x × ∆y × ∆z;

∆F(z) = 1/2∆z × (x_o × y₁ + x₁ × y_o) +1/3 × ∆x × ∆y × ∆z.

Способ долевого участия

В ряде случаев для определения величины влияния факторов на изменение результативного показателя может быть использован способ долевого участия, который применим к моделям кратно-аддитивного типа:

или

При этом сначала необходимо способом цепных подстановок определить, насколько изменился результативный показатель за счет числителя и за счет знаменателя, т. е. факторов первого порядка. Затем, зная, как факторы второго порядка повлияли на один из факторов первого порядка, можно определить их влияние на результативный показатель способом долевого участия.

Сущность его заключается в том, что доля каждого из факторов второго порядка в обобщающем их факторе первого порядка умножается на изменение результативного показателя за счет этого же фактора первого порядка.

Рассмотрим факторную модель вида y= a/b, где a и b – факторы первого порядка. В свою очередь фактор а зависит от изменения факторов второго порядка – с,d,m. Для расчета их влияния на изменение результативного показателя «у» применяют следующие формулы:

Рассмотрим пример. Рентабельность продукции (у) выросла на 8 процентных пунктов за счет увеличения на 1 тыс.руб. одного из факторов первого порядка – прибыли (∆а). При этом известно, что за счет увеличения объема продаж (d) прибыль возросла на 0,5 тыс.руб., за счет роста цен (d) прибыль возросла на 1,7 тыс.руб.,а за счет роста себестоимости продукции (m) прибыль снизилась на 1,2 тыс.руб.

Определим способом долевого участия влияние факторов второго порядка с, d и m на изменение уровня рентабельности.

=8,0×0,5/(0,5+1,7-1,2)=4,0 проц.пункта

=8,0×1,7/(0,5+1,7-1,2)=13,6 проц.пункта

=8,0×(-1,2)/(0,5+1,7-1,2)=-9,6 проц.пункта

Баланс отклонений: 4,0+13,6-9,6=8,0 процен. пункта

Лекция 1

4.8 Понятие стохастической связи

4.9 Корреляционный анализ и его значение для экономического анализа

4.10. Этапы проведения корреляционного анализа