Оптимизационные методы в принятии управленческих решений.

Многие задачи, с которыми приходится сталкивается экономисту в повседневной практике при анализе хозяйственной деятельности предприятий, многовариантны. Так как не все варианты одинаково хороши, среди множества возможных приходится отыскивать оптимальный. Значительная часть подобных задач на протяжении долгого времени решалась исходя из здравого смысла и опыта. При этом не было никакой уверенности, что найденный вариант является наилучшим.

В современных условиях даже не значительные ошибки могут привести к огромным потерям. В связи с этим возникла необходимость привлечения к анализу и синтезу экономических систем оптимизационных экономико-математических методов и ЭВМ, что создает основу для принятия научно обоснованных решений. Такие методы объединяют в одну группу под общим названием «оптимизационные методы анализа и принятия решения в экономике».

Чтобы решить экономическую задачу математическими методами, прежде всего необходимо построить адекватную ей математическую модель, т.е. формализовать цель и условия задачи в виде математических функций, уравнений и (или) неравенств.

В общем случае математическая модель оптимизационной задачи имеет вид:

max (min) : Z = Z(x) (11.1.)

при ограничениях

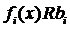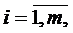, (11.2)

где:

R – отношения равенства, меньше или больше.

Если целевая функция (11.1) и функции, входящие в систему ограничений (11.2.), линейны относительно входящих в задачу неизвестных, такая задача называется задачей линейного программирования. Если же целевая функция (11.1.) или система ог­раничений (11.2.) не линейна, такая задача называется задачей линейного программирования.

В основном, на практике, задачи нелинейного программиро­вания путем линеаризации сводятся к задаче линейного про­граммирования. Особый практический интерес среди задач линейного программирования представляют задачи динами­ческого программирования, которые из-за своей многоэтапнос­ти нельзя линеаризовать. Поэтому мы рассмотрим только эти два вида оптимизационных моделей, для которых в настоящее время имеется хорошее математическое и программное обеспе­чение.

Модели и методы решения задачи линейного программирования. Среди оптимизационных моделей и методов, исполь­зуемых в теории экономического анализа, наиболее широкое распространение получили модели линейного программирова­ния, которые решаются с помощью универсального приема ­–симплексного метода. Для современных ПЭВМ имеется ряд па­кетов прикладных программ, которые позволяют решать любые задачи линейного программирования достаточно большой раз­мерности. Одновременно с решением исходной задачи указан­ные пакеты прикладных программ могут решать двойственную задачу, решение которой позволяет проводить полный экономи­ческий анализ результатов решения исходной задачи.

Решение задачи линейного программирования на ПЭВМ рас­смотрим на примере задачи об оптимальном раскрое материалов. По результатам решения проведем полный экономико-матема­тический анализ с использованием теории двойственности.

Пусть имеется 200 кг полотна шириной 86 см и 300 кг - ши­риной 89 см. Из него необходимо раскроить и сшить мужские куртки 44, 46, 52 и 54 размеров. Они должны быть изготовлены

в следующем соотношении к размерам: 44 - 25,38%; 46 ­27,88%; 52 - 24,54%; 54 - 25,54%. Итого - 100%.

Общий расход полотна, а также отходы, получаемые при рас­крое полотна, приведены в табл. 11.1 и 11.2.

Количество курток, которые выпускало предприятие в тече­ние месяца, показано в табл. 11.3.

Необходимо определить насколько рациональным оказался раскрой, а также какие размеры изделий целесообразнее раскра­ивать из полотна указанной ширины, чтобы сократить отходы.

Таблица 11.1.

Ширина полотна, см.	Размер курток
	520,27 576,42	553,5 593,49	597,4 627,2	605,6 647,77

Таблица 11.2.

Ширина полотна, см.	Размер курток
	66,27 94,45	75,5 97,49	78,4 105,7	85,6 109,7

Таблица 11.3.

Размер курток	Ширина полотна, см.

Решим данную задачу на ПЭВМ с использованием, например, инструментальных средств МВ Excel и сделаем экономический анализ полученного решения. Как правило, решение конкретной задачи на ПЭВМ включает в себя следующие этапы:

· составление математической модели;

· присвоение элементам модели определенных «имен»;

· составление матричной модели с поименованными элемен­тами;

· ввод и корректировка исходных данных;

· решение задачи на ПЭВМ;

· экономический анализ полученного решения.

Здесь х1, х2, х3, х4, х5, х6, х7, х8, обозначают соответственно количество изделий (штук) определенного размера, раскроенных из полотна шириной 86 и 89 см. Умножив количество изделий на нормы отхода, получим общую величину отходов производ­ства. Они должны быть минимальны. Тогда целевая функция имеет вид:

min: F(x) = 66,27 х1+ 75.5х2+ 78.4х3 + 95.6х4 +

+ 94.2х5 + 97.49х6+ 105.7х7+ 108.77х8.

Задача состоит в нахождении таких хj (j= 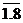), при которых целевая функция (11.1) достигнет минимума и выполняются сле­дующие условия:

520,27х1 + 553,5х2 + 597,4х3 + 605,4х4 = 200000; (11.4)

526,42х5 + 553,49х6 + 627,7х7 + 647,77х8 = 300000; (11.5)

х1 + х2 + х3 + х4 + х5 + х6 + х7 + х8 - х9 = 0; (11.6)

х1 + х5 – 0,2538х9 = 0; (11.7)

х2 +х6 – 0,2788х9 = 0; (11.8)

х3 + х7 – 0,2420х9 = 0; (11.9)

х4 + х8 – 0,2254х9 = 0; (11.10)

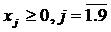. (11.11)

Здесь х9 – суммарный выпуск курток. Тогда условия (11.4) и (11.5) означают, что полотна шириной 86 см должно быть из­расходовано 200 кг, а полотна шириной 89 см - 300 кг; (11.6)­ – условие суммарного выпуска изделий; условия (11.7) – (11.10) означают сбалансированность раскроя изделий по соответствую­щим размерам; (11.11) – условие неотрицательности объемов производства.

На втором этапе каждой переменной, ограничениям, целе­вой функции и вектору ограничений (коэффициенты свободных членов) присваиваются «имена», которые должны включать не более восьми символов. Удобно, чтобы имена были информатив­ными, так как при этом облегчается использование выходных отчетов.

Элементы модели и присваиваемые им имена:

Переменная х1 х2 х3 х4 х5 х6 х7 х8 х9 Целевая функция (1.3) Ограничения по ресурсам: полотна шириной 86 см. (1.4) полотна шириной 89 см. (1.5) Общий объем производства (1.6) Ограничения по выпуску: курток размера 44 (1.7) курток размера 46 (4.8) курток размера 52(1.9) курток размера 54 (4.10) Вектор ограничений (200000, 300000, 0, 0, 0, 0, 0)

«Имя» ПР1 ПР2 ПР3 ПР4 ПР5 ПР6 ПР7 ПР8 ПР9 Отходы   Полотно 1 Полотно 2 Выпуск   Размер 44 Размер 46 Размер 52 Размер 54   Ресурсы

На третьем этапе составляем матричную модель с имено­ванными элементами модели.

На четвертом этапе введем исходные данные в ПЭВМ. При этом ввод осуществляется в соответствии с инструкцией к име­ющемуся пакету прикладных программ.

При завершении ввода исходной информации возможна ее распечатка для визуального контроля. По результатам контро­ля производится корректировка исходной информации и пере­ход на режим расчета.

Пятый этап. Решение задачи Возможно в двух режимах: решение прямой задачи; решение прямой и двойственной задач. При этом решение можно производить поэтапно, с выдачей проме­жуточных результатов алгоритма симплекс-метода, по которым можно судить о качественном процессе поиска оптимального ре­шения. По завершении результатов расчета устанавливается ре­жим распечатки (как прямой задачи, так и двойственной).

Так, в режиме расчета прямой задачи получим следующее решение, предварительно округлив результаты до целых:

ПР 1 = 150; ПР 2 = о; ПР 3 = 204; ПР 4 = о; ПР 5 = 64; ПР 6 = 235; ПР 7 = о; ПР 8 = 190; ПР 9 = 843.

Отходы = 75 743; Полотно 1 = 200 000; Полотно 2 300 = 000.

Следовательно, необходимо раскроить из полотна шириной 86 см 150 курток 44 размера и 204 куртки 52 размера, а из полот­на шириной 89 см - 64 куртки 44 размера, 235 курток 46 раз­мера и 190 курток 54 размера. Общий объем производства соста­вит 843 куртки. Суммарные отходы при таком варианте раскроя составят 75743 г, а ресурсы будут использованы полностью.

В режиме решения двойственной задачи получим значения двойственных оценок ресурсов:

Полотно 1 = 0,12996 Полотно 2 = 0,16616

Как видим, двойственные оценки объемов ресурсов отличны от нуля, следовательно, они «дефицитны». Их абсолютная ве­личина говорит о том, что увеличение объема ресурса на едини­цу приводит к качественному изменению целевой функции (11.1) на величину этой оценки. Следовательно, оценки можно счи­тать количественной мерой дефицита ресурсов: чем больше оценка, тем к большему эффекту приводит увеличение объема использования данного ресурса.

Одновременно с этим получим двойственные оценки произ­водимой продукции:

ПР 1 = о; ПР 2 = 4,70818; ПР 3 = о; ПР 4 = 4; ПР 5 = о; ПР 6 = о; ПР 7 = 0,73815; ПР 8 = о.

Здесь двойственные оценки ПР 2, ПР 4, ПР 7 принимают ну­левые значения. Абсолютные значения этих оценок говорят о том, что если мы все же будем раскраивать соответствующие изделия, потери от отходов будут только увеличиваться на ве­личину оценки от раскроя одной единицы изделия. Следова­тельно, раскраивать куртки 46 и 54 размеров из полотна 86 см нецелесообразно, точно так же как и куртки 52 размера - из по­лотна шириной 89 см.

Теперь сопоставим нормативные отходы при традиционном ва­рианте раскроя с отходами при оптимальном варианте (табл. 11.4).

Таблица 11.4.

Размеры	Отходы на ед. по норме ,г.	Фактический выход изделий, шт.	Отходы при фактич. выпуске, (гр.2*гр.3), г.	Оптимальный выход изделий, шт.	Отходы при оптим. выпуске (гр.2*гр.3), г.	Отклонения
количество, шт.	отходы, г.
Ширина полотна 86 см
	66,27 75,5 78,4 85,6 94,45		5301,6 8305,0 7526,4 5649,6 12649,6		9940,5 15993,6	+70 +110 +108 -66 -70	+4638,9 8305,0 +8467,2 5649,6 -66,0672
Ширина полотна 89 см
	97,49 105,7 109,77		12186,25 11415,6 13611,48		22910,15 20856,42	+110 -108 +66	+10723,9 -11415,6 +7244,82
Всего		76645,53		75743,42	–	-902,1

Из таблицы видно, что наиболее рационален раскрой из по­лотна шириной 86 см изделий 44 и 52 размеров, а из полотна шириной 89 см - 44, 46 и 54 размеров. Такой способ раскроя уменьшает отходы, увеличивает выпуск изделий, прибыль предприятия и его рентабельность.

Отметим, что в современных пакетах прикладных программ для решения задач линейного программирования симплекс-ме­тодом предусмотрены режимы расчета так называемых интер­валов устойчивости, как для ограниченных ресурсов, так и для переменных величин, принимающих ненулевые значения. Эко­номический смысл этих интервалов состоит в том, что измене­ние объемов ресурсов и значений переменных в пределах этих интервалов не изменяет структуру оптимального плана. Это позволяет предприятию проводить рациональную политику приобретения дополнительных ресурсов.