Определение ставки процентов

Для того, чтобы найти ставку i, необходимо решить одно из нелинейных уравнений (опять предполагаем, что речь идет о постоянной годовой ренте постнумерандо) следующего вида

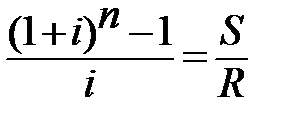или .

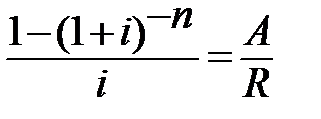Решить такие уравнения можно несколькими способами. Рассмотрим наиболее распространенные из них: метод линейной интерполяции и метод Ньютона-Рафсона.

Метод линейной интерполяции состоит в том, что сначала методом подбора ищут примерную оценку верхней и нижней ставки i. Затем эти найденные ставки подставляют в уравнение и сравнивают с правой его частью. Далее производится корректировка нижнего значения ставки по следующей формуле:

,

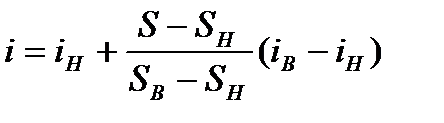где S_в и S_н – значение коэффициента наращения (или коэффициента приведения) ренты для процентных ставок i_в и i_н.

Затем скорректированное нижнее значение ставки подставляют в формулу и сравнивают его с правой частью. Если достигнутой точности недостаточно, повторно корректируют нижнее значение ставки (с заменой приближенной оценки ставки на более точную) по выше указанной формуле и так до момента, когда необходимая точность не будет достигнута.

Метод Ньютона-Рафсона также подразумевает подборку оценок. Этот метод разработан для нелинейных уравнений вида ƒ(х) = 0.

В данном методе алгоритм поиска приемлемого решения сводится к трем операциями на каждом шаге, которые зависят от типа ренты и исходных заданных величин.

Сначала будем считать, что известна наращенная сумма S и найдена какая-то начальная оценка процентной ставки (например, методом проб).

Если рассматривать постоянную годовую ренту постнумерандо с начислением процентов один раз в конце года (p=1, m=1), то необходимо решить следующее уравнение:

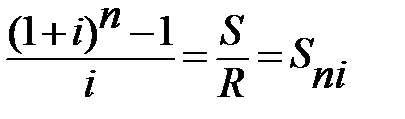или .

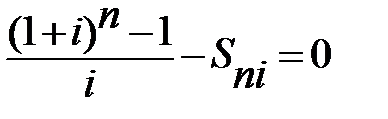Алгоритм уточнения оценки на каждом шаге k будет следующим:

, , .

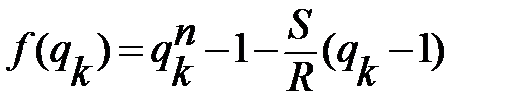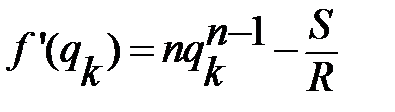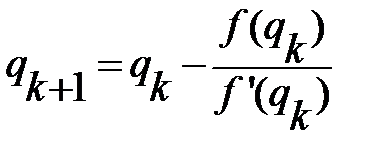Если рассматривать постоянную р-срочную ренту постнумерандо с начислением процентов один раз в конце года (p≥1, m=1), то необходимо решить следующее уравнение:

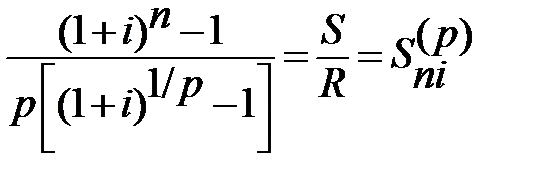или .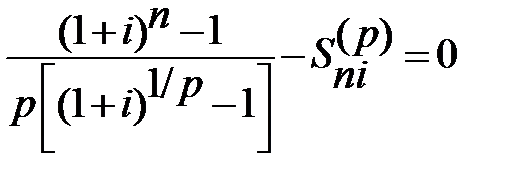

Алгоритм уточнения оценки на каждом шаге k будет следующим:

,

,

.

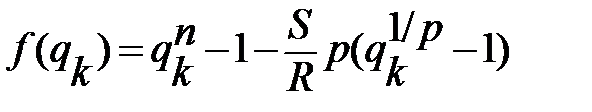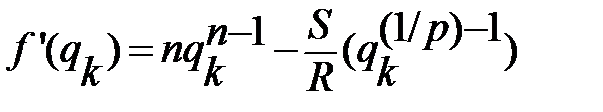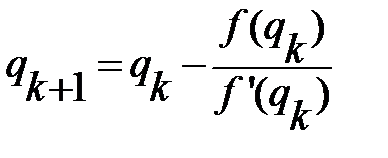Примечание:

Начальную оценку q_o = 1+i_o следует выбирать такой, чтобы соответствующий ей множитель наращения был максимально приближен к значению S/R. Это обеспечит сходимость алгоритма и сократит количество итераций. Вычисления прекращаются, как только будет достигнута приемлемая точность при сравнении множителя наращения и отношения S/R.

Теперь будем считать, что известна современная сумма A и найдена какая-то начальная оценка процентной ставки (например, методом проб).

Если рассматривать постоянную годовую ренту постнумерандо с начислением процентов один раз в конце года (p=1, m=1), то необходимо решить следующее уравнение: 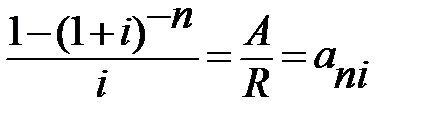или .

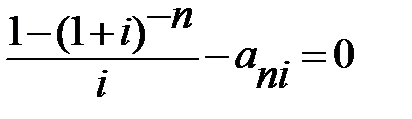Алгоритм уточнения оценки на каждом шаге k будет следующим:

,

,

.

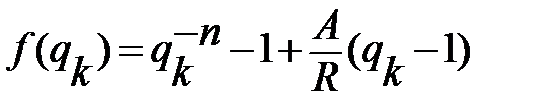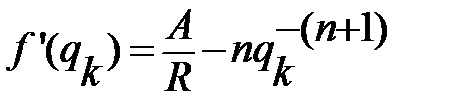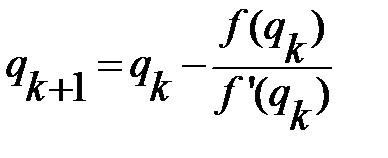Если рассматривать постоянную р-срочную ренту постнумерандо с начислением процентов один раз в конце года (p≥1, m=1), то необходимо решить следующее уравнение:

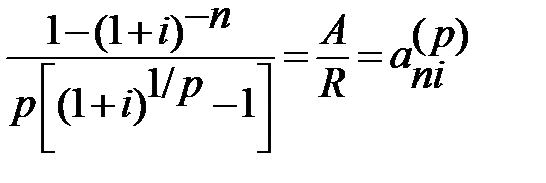или .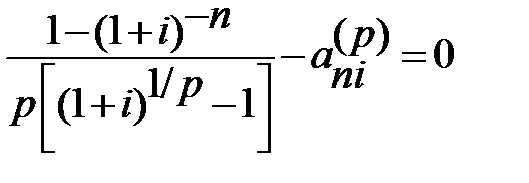

Алгоритм уточнения оценки на каждом шаге k будет следующим:

,

,

.

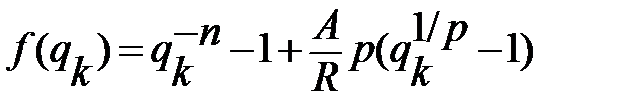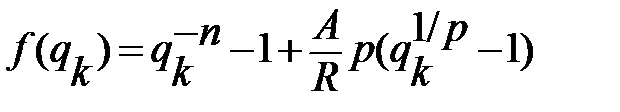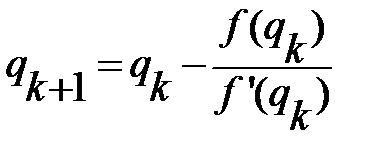Вопросы для самопроверки:

1. Дайте определение финансовых рент.

2. Классифицируйте финансовые ренты.

3. Что такое аннуитет?

4. Приведите примеры финансовых операций, денежные потоки которых представляют собой аннуитет.

5. Поясните, что такое приведенная стоимость денежного потока?

6. В чем отличие между рентами постнумерандо, пренумерандо, муннумерандо.

Тема 6.1. Основные способы погашения долга. Методы расчета платежей при погашении долга. Составление плана погашения долга.

Вопросы для рассмотрения:

1. Понятие и финансово-экономические условия кредита.

2. Погашение долга равными суммами основного долга.

3. Погашение долга равными суммами уплатами при известном сроке.

4. Погашение долга равными суммами уплатами при неизвестном сроке.

Составление планов погашения кредитов

Основная задача расчетов по кредиту – выбор и согласование метода определения срочных выплат процентов и основного долга.

Погашение задолженности может осуществляться единовременным платежом в конце срока займа или частичными платежами.

Рассмотрим случай погашения задолженности частичными платежами.

1.Погашение долга равными суммами основного долга.

Основной долг – D, срочная уплата – P, состоит из b – величины основного дола и величины процентов, n – срок, р – число платежей в году.

Формулы: периодическая величина основного долга .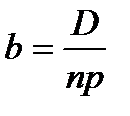

Срочная уплата: 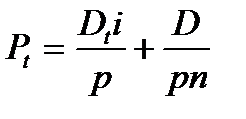, здесь 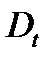– остаток задолженности.

Пример: клиент банка получил кредит 120 тыс.р., сроком на 1 год с ежемесячными платежами в конце каждого года, ставка 15% годовых. Составить план погашения кредита.

Месяцы	Остаток долга на начало месяца	Сумма погашения основного долга	Сумма выплат процентов	Сумма срочных уплат
			1,5	11,5
			1,375	11,375
			1,25	11,25
			1,125	11,125
			0,875	10,875
			0,75	10,75
			0,625	10,625
			0,5	10,5
			0,375	10,375
			0,25	10,25
			0,125	10,125
Итого			9,75	129,75

2.Погашение долга равными суммами уплатами.

а) известен срок займа

Срочная уплата равна: .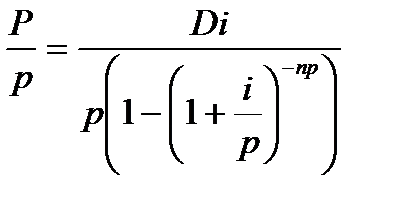

Сумма погашения основного долга: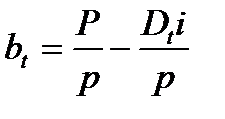

Пример: клиент получил кредит 10 тыс.р. на 3 года по ставке 12% годовых с условием погашения годовыми выплатами.

Год	Остаток долга на начало года	Сумма погашения основного долга	Сумма выплат процентов	Сумма срочных уплат
		2,96348981	1,2	4,16348981
	7,03651019	3,31910858	0,84438	4,16348981
	3,71740161	3,71740161	0,44609	4,16348981
Итого			2,49047	12,4904694

б) задана величина срочного платежа

Определяем срок: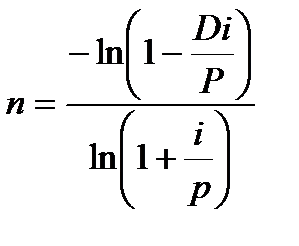

Пример:кредит на сумму 15 тыс. р. выдан под 12% годовых. Срочные уплаты 4 млн.руб. Рассчитать план погашения кредита, если платежи выплачиваются 1 раз в год, 2 раза в год. Получаем: n=5,3 года.

Год	Остаток долга на начало года	Сумма погашения основного долга	Сумма выплат процентов	Сумма срочных уплат
		2,2	1,8
	12,8	2,464	1,536
	10,336	2,75968	1,24032
	7,57632	3,0908416	0,9091584
	4,4854784	3,461742592	0,538257408
	1,023735808	1,023735808	0,122848297	1,146584105
Итого			6,146584105	21,1465841

Год	Остаток долга на начало года	Сумма погашения основного долга	Сумма выплат процентов	Сумма срочных уплат
		1.1	0.9
	13.9	1.166	0.834
	12.734	1.23596	0.76404
	11.49804	1.3101176	0.6898824
	10.1879224	1.38872466	0.61127534
	8.79919774	1.47204814	0.52795186
	7.32714961	1.56037102	0.43962898
	5.76677859	1.65399328	0.34600672
	4.1127853	1.75323288	0.24676712
	2.35955242	1.85842685	0.14157315
	0.50112556	0.50112556	0.03006753	0.5311931
Итого			5.5311931	20.5311931

3. Погашение займа переменным выплатами основного долга

а) Выплаты изменяются в арифметической прогрессии

Предположим, что контрактом предусмотрено погашение основного долга производить платежами, возрастающими или убывающими в арифметической прогрессии с разностью d. В этом случае выплаты основного долга составят R, R+d, … по годам. В последний год соответственно R+(n-1)d.

Величина основного долга равна сумме всех выплат, т.е. сумме чле­нов возрастающей арифметической прогрессии: 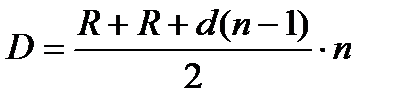. Найдем из этого уравнения :

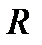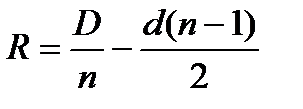
Пример: Кредит размером 4,0 млн. р. выдан на 5 лет под 15% годовых с начислением процентов в конце каждого расчетного периода (года). Выплаты основного долга должны возрастать ежегодно на 0,1 млн руб.

Год	Остаток долга на начало года	Сумма погашения основного долга	Сумма выплат процентов	Сумма срочных уплат
		0,6	0,6	1,2
	3,4	0,7	0,51	1,21
	2,7	0,8	0,405	1,205
	1,9	0,9	0,285	1,185
	1,0		0,15	1,15
Итого	-		1,95	5,95

б) Выплаты изменяются в геометрической прогрессии

Одним из вариантов погашения кредитной задолженности может быть такой, при котором погашение основного долга должно произ­водиться платежами, каждый из которых больше или меньше преды­дущего в qраз. Таким образом, эти платежи будут являться членами возрастающей или убывающей геометрической прогрессии. Члены этой прогрессии будут иметь вид: 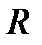, , 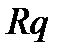, 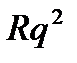… . Основной долг – сумма этих членов, т.е. 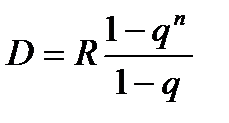, откуда 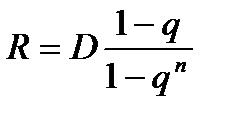(первый платеж по основному долгу).

Пример.Кредит в размере 300,0 тыс. долл. должен быть погашен в течение шести лет ежегодными выплатами. Процентная ставка 15% годо­вых, начисление процентов один раз в конце года. Платежи, обеспечиваю­щие погашение основного долга, должны увеличиваться в геометрической прогрессии на 5% ежегодно. Составить план погашения кредита.

Год	Остаток долга на начало года	Сумма погашения основного долга	Сумма выплат процентов	Сумма срочных уплат
		44,1052	45,0000	89,1052
	255,8948	46,3105	38,3842	84,6947
	209,5843	48,6260	31,4376	80,0636
	160,9583	51,0573	24,1437	75,2010
	109,9010	53,6102	16,4852	70,0954
	56,2907	56,2907	8,4436	64,7343
Итого	-		163,8942	463,8942

Конверсия займов

Конверсия займа – изменение условий погашения кредитов называется конверсией займа. При достижении соглашения о конверсии могут изменяться срок погашения займа, процентная ставка, порядок годовых выплат и т.п.

При любом методе конверсии первоначально определяются сумма выплаченного основного долга и величина непогашенной его части.

Непогашенная часть долга рассматривается как новый долг, под­лежащий уплате на новых условиях.

Рассмотрим один из вариантов конверсии, когда изменяются срок погашения займа и процентная ставка, а срочные уплаты как по ста­рым, так и по новым условиям производятся равными платежами; про­центы начисляются один раз в конце каждого расчетного периода.

Обозначим параметры займов: первоначальный срок погашения займов до конверсии; срок, на который продлен период погашения в резуль­тате конверсии; число оплаченных расчетных периодов до конверсии; процентная ставка до конверсии; процентная ставка после конверсии; величина срочной уплаты до конверсии; величина срочной уплаты после конверсии; величина основного долга; остаток долга на момент конверсии.

Для составления плана погашения конверсионного займа опре­деляют:

1) величину срочной уплаты по старым условиям: .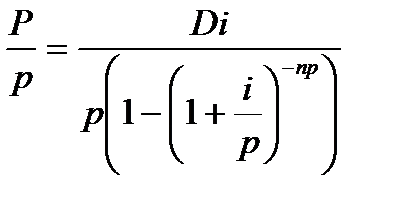

2) остаток долга на момент конверсии: .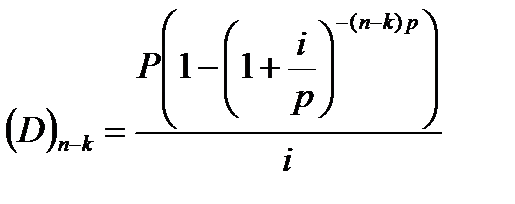

3) величину срочной уплаты по новым условиям: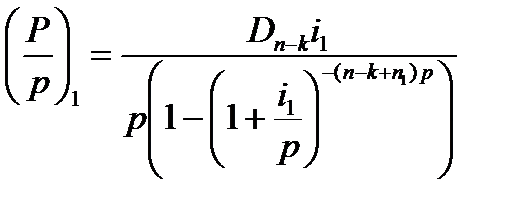

Пример.Кредит в сумме 40,0 тыс. долл., выданный на 5 лет под 6% го­довых, подлежит погашению равными ежегодными выплатами в конце каж­дого года. Проценты начисляются в конце года. После выплаты третьего платежа достигнута договоренность между кредитором и заемщиком о про­длении срока погашения займа на 2 года и увеличении процентной ставки с момента конверсии до 10%. Необходимо составить план погашения остав­шейся части долга.

Величина срочной уплаты по старым условиям: 9,4959 тыс. долл.

Остаток долга на момент конверсии: 17,4097 тыс. долл.

Величина срочной уплаты по новым условиям: 5,4923 тыс. долл.

План погашения на конверсированный кредит:

Год	Остаток долга на начало года	Сумма погашения основного долга	Сумма выплат процентов	Сумма срочных уплат
	17,4097	3,7513	1,7410	5,4923
	13,6584	4,1265	1,3658	5,4923
	9,5319	4,5391	0,9532	5,4923
	4,9928	4,9930	0,4993	5,4923
Итого	-	17,4099	4,5593	21,9692

Проверим правильность расчетов: сумма выплат по основному долгу до конверсии и сумма выплат после должны быть равны в сумме 40 тыс.долл.

R₁=9,4959-40*0,06= 7,0959 тыс. долл.

R₂= 7,0959 • 1,06 = 7,5217 тыс. долл.

R₃= 7,5217 • 1,06 = 7,9730 тыс. долл.

(помним формулу: 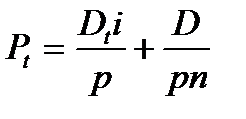, здесь 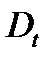– остаток задолженности)

7,0959+7,5217+7,9730=22,5906

17,41+22,59=40 тыс. долл.

Порядок действий при других условиях конверсии аналогичен.

Консолидация займов

В финансовой практике может возникнуть ситуация, когда кре­дитору, предоставившему несколько займов одному заемщику, более удобно или выгодно объединить эти займы в один, т.е. произвести их консолидацию. В случае согласия обеих сторон первым шагом при консолидации займов является нахождение величин остатков каждого долга. Рассчитав остатки долгов и просуммировав их, получают объединенный долг, на который составляется новый план погашения.

Пример.Банком было предоставлено предприятию два кредита. Первый, в размере 2,0 млн руб. под 8% годовых, должен погашаться равными полугодовыми выплатами в течение 6 лет, начисление процентов – по полугодиям. Второй – 1,5 млн руб. со сроком погашения 4 года, ставка 12%, капитализация ежегодная.

После выплаты в течение двух лет два долга объединяются в один на следующих условиях: консолидированный долг имеет срок погашения 8 лет, погашение производится равными полугодовыми срочными выплатами, процентная ставка 14%, капитализация полугодовая. Определить величину полугодовой срочной уплаты.

Срочная уплата первого займа: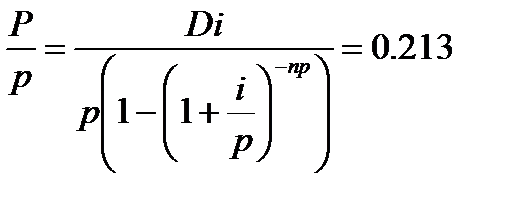

Остаток первого основного долга после двух лет его погашений (четыре срочные уплаты):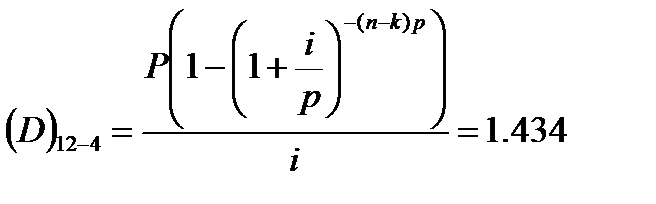

Срочная уплата второго займа: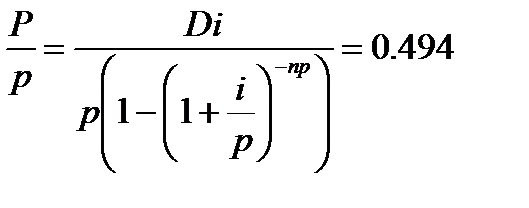

Остаток второго основного долга после двух лет его погашений (две срочные уплаты):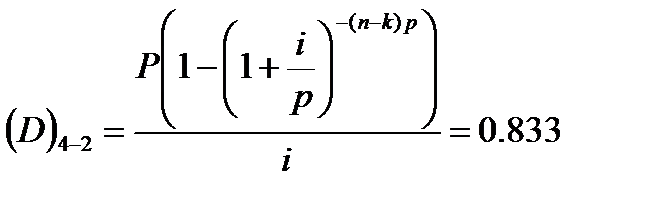

Общая величина непогашенных основных долгов после двухго­дичных выплат:

1,434 + 0,833= 2,267 млн. р.

Срочная уплата консолидированного займа:

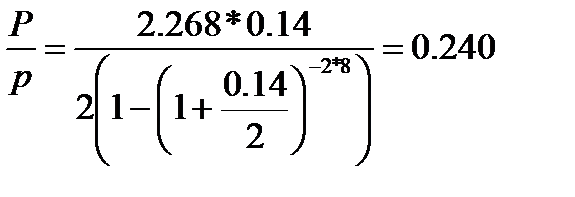
Вопросы для самопроверки:

1. Что такое кредит?

2. Назовите основную задачу расчетов по кредиту.

3. Какими способами может осуществляться погашение займа?

4. Что представляет собой конверсия займа?

5. Что представляет собой консолидация займа?