Дисконтирование по формуле сложных процентов.
Дисконтирование по сложным процентам осуществляется по формуле:
.
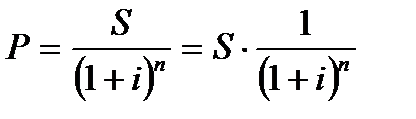Вопросы для самопроверки:
1. В чем отличие сложных процентов от простых?
2. В каких случаях целесообразно применение сложных процентов?
3. Что такое множитель наращения? В чем заключается его экономический смысл?
4. Какую процентную ставку называют силой роста?
5. Перечислите виды начисления процентов в зависимости от частоты начисления.
Тема 3.1.-3.2. Понятие эквивалентности процентных ставок. Вывод формул эквивалентности процентных ставок на основе равенства множителей наращения. Принцип финансовой эквивалентности обязательств. Уравнение эквивалентности. Объединение (консолидация) платежей.
Вопросы для рассмотрения:
1. Эквивалентность процентных ставок. Общие принципы.
2. Эквивалентность простой и сложной процентной ставки с начислением процентов 1 раз в год.
3. Эквивалентность простой процентной ставки и сложной с начислением процентов m раз в год.
4. Эквивалентность сложной процентной ставки с начислением процентов 1 раз в год и сложной процентной ставки с начислением процентов m раз в год.
5. Эквивалентность непрерывной процентной ставки и простой процентной ставки.
6. Эквивалентность непрерывной процентной ставки и сложной процентной ставки с начислением 1 раз в год.
7. Эквивалентность непрерывной процентной ставки и простой процентной ставки с начислением m раз в год.
8. Средняя процентная ставка.
9. Финансовая эквивалентность обязательств.
1. Принцип финансовой эквивалентности обязательств
В финансовой практике часто возникают ситуации, когда необходимо заменить одно обязательство другим, например, с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи), изменить схему начисления процентов и т. п. Таким общепринятым принципом, на котором базируются изменения условий контрактов, является финансовая эквивалентность обязательств.
Изменение условий контракта основывается на принципефинансовой эквивалентности обязательств, который позволяет сохранить баланс интересов сторон контракта. Этот принцип предполагает неизменность финансовых отношений до и после изменения условий контракта. При изменении способов начисления процентов необходимо учитывать взаимозаменяемость между различными видами процентных ставок.
Эквивалентными называются процентные ставки, которые при замене одной на другую приводят к одинаковым финансовым результатам, т.е. отношения сторон не изменяются в рамках одной финансовой операции.
При изменении условий платежей также необходимо учитывать разновременность платежей, которые производятся в ходе выполнения условий контракта до и после его изменения. Эквивалентными считаются такие платежи, которые оказываются равными после их приведения по заданной процентной ставке к одному моменту времени, либо после приведения одного из них к моменту наступления другого по заданной процентной ставке.
Приведение осуществляется путем дисконтирования (приведение к более ранней дате) или, наоборот, наращения суммы платежа (если эта дата относится к будущему).
Если при изменении условий контракта принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить.
2. Эквивалентность процентных ставок
Для нахождения значений эквивалентных процентных ставок следует составлять уравнение эквивалентности.
Эквивалентность простой процентной и простой учетной ставок.Исходные уравнения для вывода эквивалентности
S = P(1 + n ∙ i) и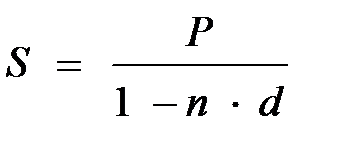 
Если результаты наращения равны, то получаем уравнение
P (1 + n ∙ i) =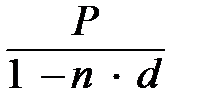 
.
Отсюда 1 + n ∙ i =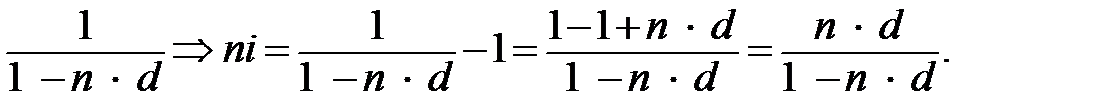 
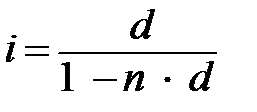и 
.
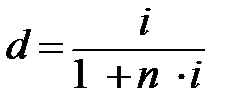Для одних и тех же параметров ссуды условие эквивалентности приводит к тому, что d<i. При этом с ростом срока финансовой операции различие между ставками увеличивается.
Пример 1. Определить простую учетную ставку, эквивалентную ставке обычных процентов 12 % годовых, при наращении за 2 года.
Решение. Параметры задачи: n = 2 года, i= 12 %. Тогда
d = 0,12/(1 + 2 ∙0,12) = 0,0968 или 9,7 %.
Следовательно, операция, в которой принята учетная ставка 9,7 %, дает тот же финансовый результат для 2-годичного периода, что и простая ставка 12 % годовых.
Эквивалентность простой и сложной процентных ставок. Наращенные суммы по простой и сложной процентным ставкам равны
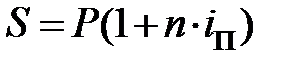и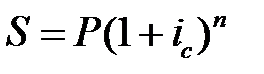 
.
Если равны результаты наращения, то уравнение эквивалентности
= 
.
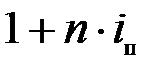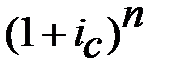Отсюда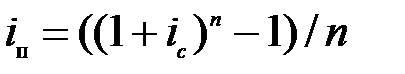 
и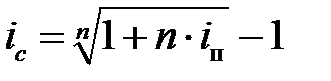 
.
При начислении процентов m раз в году аналогично рассуждая, получим: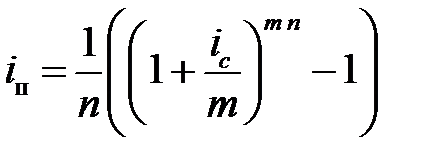 
и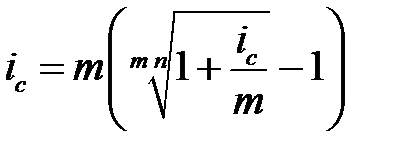 
.
Пример 2. Предполагается поместить капитал на 4 года либо под сложную процентную ставку 20 % годовых с полугодовым начислением процентов, либо под простую процентную ставку 26 % годовых. Найти оптимальный вариант.
Решение. Параметры задачи: n = 4 года, m = 2, iс = 20 %, iп = 26 %. Находим для сложной процентной ставки эквивалентную простую ставку:
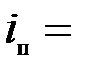
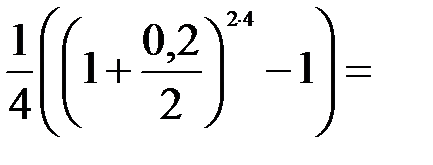0,285 9 или 28,59 %.
Таким образом, эквивалентная сложной ставке, по первому варианту, простая процентная ставка составляет 28,59 % годовых, что выше предлагаемой простой ставки в 26 % годовых по второму варианту. Следовательно, выгоднее разместить капитал по первому варианту, т.е. под 20 % годовых с полугодовым начислением процентов.
Пример 3.По трёхмесячному депозиту назначена ставка 10,2 % годовых. Какую ставку годовых процентов следует назначить на ежемесячные депозиты, чтобы последовательное переоформление этих депозитов привело к такому же результату, что и использование трёхмесячного депозита, если пренебречь двумя днями, которые теряются при переоформлении депозитов (T=360)?
Решение. Приравняем соответствующие множители наращения:
.
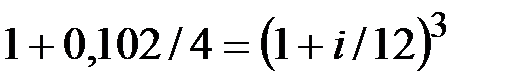Отсюда получаем, что i= 0,101 1 или 10,11 %.