Оценка риска с помощью леммы Маркова

И неравенства Чебышева

Одним из приемов получения оценки уровня риска или надежности в виде показателя вероятности может оказаться использование леммы Маркова. Уровень вероятности в этом случае определяется не очень четко, поэтому прибегать к данному приему следует в силу крайней необходимости, когда других способов более точной оценки уровня риска нет.

Лемма Маркова позволяет находить нижнюю границу вероятности того, что случайная величина Х не превысит некоторого, заранее заданного значения a. Она имеет следующий вид:

.

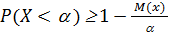Чтобы использовать лемму Маркова при оценке риска инвестиционных операций, в качестве Х необходимо взять такой показатель финансового состояния получателя инвестиций (объекта вложений), от которого в значительной мере зависит его платежеспособность, а значит, и благополучный возврат инвестиций.

Для промышленного предприятия таким показателем может быть коэффициент текущей ликвидности (КТЛ). В качестве величины a при этом можно будет взять пограничное значение КТЛ, равное 2. Предприятия с меньшим значением КТЛ должны считаться утратившими платежеспособность.

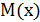в приведенном выше неравенстве обозначает математическое ожидание случайной величины. В качестве его в нашем случае следует взять среднее значение показателя, принятого за основу оценки платежеспособности получателя инвестиций.

Если мы возьмем в качестве такого показателя КТЛ, то после соответствующей подстановки выражение 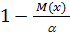будет отвечать на вопрос, чему как минимум равна вероятность потери средств, инвестированных в предприятие с тем или иным средним значением КТЛ.

Пример 2.8.

Оценить вероятность того, что инвестор может потерять свои средства, вложенные в предприятие, у которого среднее значение КТЛ составило 1,6.

Решение.

Используем лемму Маркова, предположив, что инвестиции будут потеряны, если КТЛ у объекта инвестиций останется ниже 2.

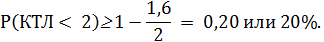
Достоинством леммы Маркова является то, что при ее использовании не накладывается никаких ограничений ни на возможный вид распределения вероятностей, ни на объем исходных данных.

Рассмотрим возможности использования неравенства Чебышева для оценки риска. Неравенство Чебышева имеет следующий вид:

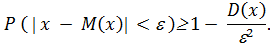
Неравенство говорит о том, что вероятность отклонения случайной величины Х от своего математического ожидания на величину, меньшую e, будет больше 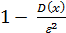. Вероятность противоположного события при этом будет определяться так:

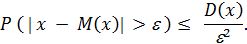
Пример 2.9.

Динамика КТЛ у предприятия, ожидающего инвестиций, за пять прошлых месяцев имеет следующий вид.

Месяц
Значение КТЛ	1,8	1,5	1,4	1,7	1,6

Найти вероятность того, что предприятие восстановит свою платежеспособность и погасит долг перед инвестором.

Решение.

Среднее значение КТЛ по этим данным составит:

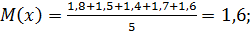
а дисперсия будет равна:

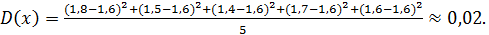
Определим вероятность того, что предприятие восстановит свою платежеспособность. Чтобы это произошло, КТЛ у предприятия должен вырасти и достичь величины 2, т.е. он должен будет отклониться от своего нынешнего среднего значения, равного 1,6, как минимум на 0,4, причем в большую сторону.

Вероятность отклонения случайной величины (здесь КТЛ) от своего среднего значения, равного 1,6, на величину большую 0,4 в обе стороны (и большую, и меньшую) равна:

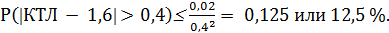
Вероятность отклонения в одну (большую) сторону будет не более:

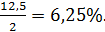
Итак, вероятность восстановления предприятием своей платежеспособности и возврата долга инвестору равна не более 6,25%. Значит, вероятность противоположного события, когда инвестор потеряет свои средства, вложенные в ненадежное предприятие, будет равна не меньше .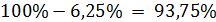

Достоинством неравенства Чебышева является то, что на его использование не накладывается каких-либо ограничений в части вида распределения вероятностей и объема исходных данных.