Детерминированый факторный анализ. Способы оценки влияния факторов в детерминированом факторном анализе

При проведении детерминированного факторного анализа наиболее часто встречаются 4 типа факторных моделей (рис. 19):

Рис. 19.Типология моделей, применяемых при проведении детерминированного

факторного анализа

1. Аддитивные модели - используются в случаях, когда результативный показатель можно представить как алгебраическую сумму величин нескольких факторных показателей:

Y = X1 + X2 + X3 + … + Xn

2. Мультипликативные модели - применяются тогда, когда результативный показатель представляет собой произведение величин нескольких факторов:

Y = X1* X2 * X3* … *Xn

3. Кратные модели - представляют собой ситуацию, когда результативный показатель получают в результате деления величины одного фактора на величину другого:

Y = X1 / X2

4. Смешанные (комбинированные) модели – это сочетание ранее перечисленных моделей в различных комбинациях. Например:

a+b a

Y = ----- ; Y = ----- ; Y = (a + b) * c… и другие.

c b+c

В детерминированном факторном анализе для измерения влияния факторов на результативный показатель используются различные методы (способы), каждый из которых имеет свои преимущества и недостатки (рис. 20):

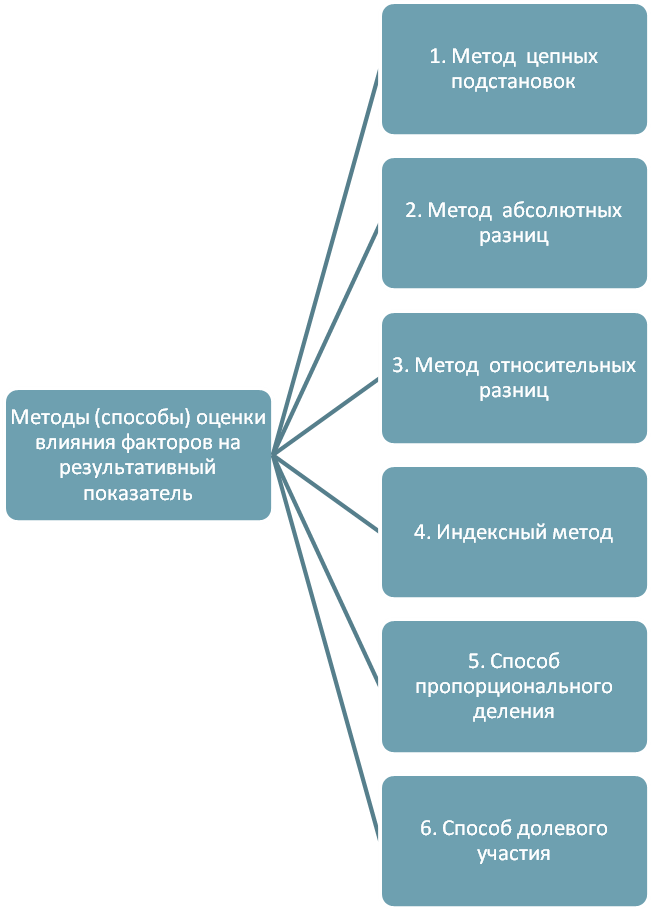
Рис. 20.Типовая классификация методов (способов) оценки влияния факторов на результативный показатель

Существуют и другие методы (способы) измерения влияния факторов на результативный показатель, однако они мало применяются на практике и достаточно сложны в своем использовании. В свою очередь, среди методов, представленных на рис. 20, наиболее часто применяются метод цепных подстановок, метод абсолютных разниц, а также метод относительных разниц.

1. Метод цепных подстановок- используется наиболее часто и является наиболее универсальным из всех методов. Указанный способ позволяет измерить влияние каждого отдельного фактора на прирост результативного показателя. Данный способ применяется в случае, если между изучаемыми показателями имеет место определенная функциональная зависимость.

Суть способа цепных подстановок заключается в последовательной замене базисной величины каждого фактора отчетными значениями и в последующей оценке влияния произведенной замены на результативный показатель. Данный способ основан на методе элиминирования.

Элиминирование - означает устранение влияния всех других факторов (кроме одного), то есть все остальные факторы остаются статичными (неизменными). Следует отметить, что, если в факторной модели присутствуют как количественные, так и качественные факторы, то замену факторов необходимо начинать с количественного фактора, который считается наиболее важным по сравнению с качественным.

Алгебраическая сумма влияния факторов должна быть равна приросту величины результативного показателя. Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах. По окончании расчетов определяется удельный вес (доля) влияния каждого фактора на результативный показатель как отношение влияния каждого фактора к совокупному отклонению.

Способ абсолютных разниц

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

Порядок аналитических расчетов на примере четырехфакторной мультипликативной модели выглядит следующим образом:

Yo ⁼ Ао * Bо* Cо* Dо

Y1 = A1* B1* C1 *D1

Расчеты влияния исследуемых факторов можно представить в следующем виде:

∆ Y (A) = ∆A * Bo* Co* Do

∆ Y (B) = ∆B * A1* Co* Do

∆ Y (C) = ∆C * A1* B1* Do

∆ Y (D) = ∆D * A1 * B1* C1

По окончании расчетов исчсляют общий баланс отклонений по следующей формуле:

∆Y = Y1 - Yo = ∆Y(A) + ∆Y(B) + ∆Y(C) + ∆Y(D)

3. Способ относительных разниц - заключается в проведении двух последовательный вычислительных операций. Первая операция заключается в определении относительных отклонений по каждому факторному показателю, а вторая операция связана с определением влияния изменения каждого фактора на результативный показатель.

Для примера используем вышеприведенную четырехфакторную функциональную зависимость:

Yo = Ao* Bo * Co * Do

Y1 = A1* B1 * C1 * D1

Первая операция по первому фактору состоит в вычислении процентного отношения по формуле:

∆ A( %) = ( Ai – Ao)/ Ao * 100 и т.д.

Расчет влияния изменения каждого фактора на результативный показатель (вторая операция) осуществляют по следующим формулам:

∆ Y (A) = Yo * A (%) : 100

∆ Y (B) = (Yo + ∆Y (A)) * ∆B % : 100

∆ Y (C) = (Yo + ∆Y(A) + ∆ Y(B)) * ∆C % : 100

∆ Y (D) = (Yo + ∆Y(A) + ∆Y (B) + ∆Y (C)) * ∆D % : 100

4. Индексный метод - основан на применении специальных индексов (от лат. слова «index» - показатель, указатель). В свою очередь, индекс - это показатель сравнения двух состояний одного и того же явления, индексируемая величина - это признак, изменение которого изучается.

Каждый индекс включает два вида данных:

- оцениваемые данные, имеющие название «отчетные» и обозначаемые значком «1»;

- данные, которые используются в качестве базы сравнения – «базисные»
обозначаемые знаком «0».

В экономическом анализе используются различные виды индексов (рис. 21):

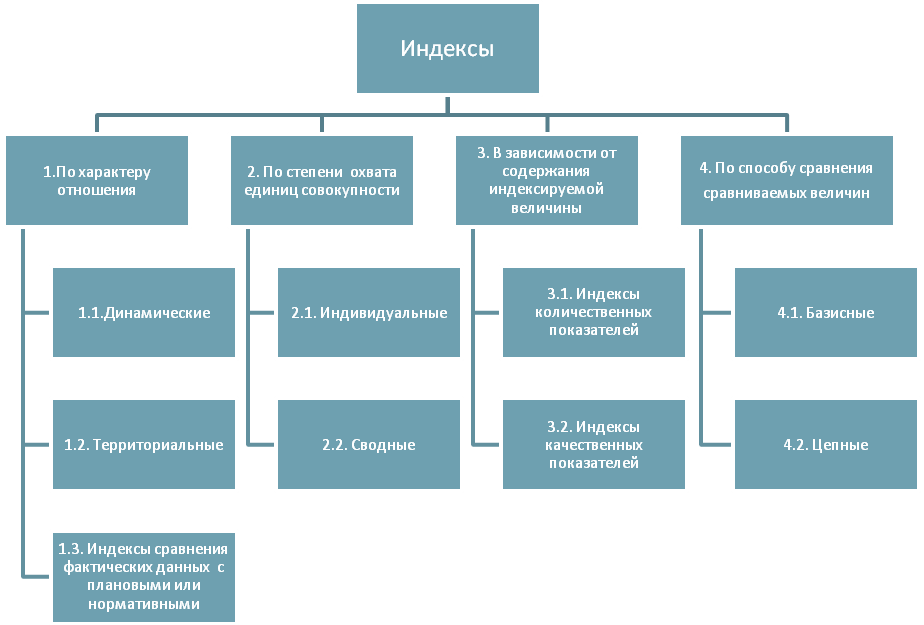
Рис. 21. Типовая классификация индексов, применяемых

в экономическом анализе

1.1. Динамические индексы - предусматривают сравнение изучаемых явлений во времени. При применении динамического индекса в качестве базы сравнения используют показатель предыдущего периода.

1.2. Территориальные индексы - используют для сравнения изучаемых явлений в пространстве.

1.3. Индексы сравнения фактических показателей с плановыми (нормативными) - применяются для оценки выполнения плановых заданий, договорных обязательств, а также нормативных показателей.

2.1.Индивидуальные индексы ( i ) - показывают изменение отдельных показателей или одного элемента статистической совокупности. К ним, например, относят:

- индивидуальный индекс цен (i _{pi ) :}

i _pi = _p1i /_p0i, где:

- p_0i - цена единицы продукции i-го вида базисного периода;_длдлдлдлдл_-

_jkjkjkjkj=jkjkjkjkjkjkjp1pppp- цен

- p_1i - цена единицы продукции i–го вида отчетного периода.

- индивидуальный индекс физического объема производства (I _qi) :

i _qi = q_1i / q_0i , где:

- q_0i ^- объем производства продукции i–го вида базисного периода;

- q_1i- объем производства продукции i-го отчетного периода.

- индекс себестоимости (i ^c):

i _сi = c_1i /c_0i , где:

с _0i и с _1i- индекс себестоимости продукции i-го вида, соответственно, базисного и отчетного периодов.

2.2. Сводные индексы ( I ) - отражают изменение по всей совокупности элементов сложного явления. Примерами сводных индексов являются:

- общий агрегатный индекс цен (индекс Пааше), схему построения которого предложил немецкий экономист Г. Пааше (1874 г.):

∑ q¹ p ¹

_{i i}

I p = ---------------

∑ q¹p⁰

_{i i}

Разница между числителем и знаменателем формулы означает изменение выручки от продаж в результате среднего изменения цен в отчетном периоде по сравнению с базисным.

- базовый взвешенный индекс цен (индекс Ласпейреса, схему построения которого предложил немецкий экономист Э. Ласпейрес (1864 г.):

∑ q⁰ p¹

^{i i}

I p = ------------

∑ q⁰p⁰

_{i i}

Индекс Ласпейреса определяет влияние изменения цен при условии продаж такого же количества товаров, как в базисном периоде.

3.1. Индексы количественных (объемных) показателей - характеризуют весь объем статистической совокупности (например, индекс физического объема продукции).

3.2. Индексы качественных показателей - характеризуют отдельную единицу статистической совокупности. Например, индексы цен, себестоимости.

4.1. Базисные индексы - получают путем сопоставления с уровнем периода, принимаемого за базу сравнения.

4.2. Цепные индексы – получают путем сопоставления текущих уровней с предшествующими.