Проценты и процентные ставки
Логика построения основных алгоритмов достаточно проста и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы P с условием, что через какое-то время t будет возвращена большая сумма S. Как известно, результативность подобной сделки может быть охарактеризована двояко: либо с помощью абсолютного показателя – прироста (S-P), либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом – ставкой. Этот показатель рассчитывается отношением приращения исходной суммы к базовой величине, в качестве которой можно брать либо P, либо S. Таким образом, ставка рассчитывается по одной из двух формул:
темп прироста 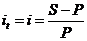 ; (1.1)
; (1.1)
темп снижения 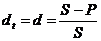 . (1.2)
. (1.2)
В финансовых вычислениях первый показатель имеет также названия: "процентная ставка", "процент", "рост", "ставка процента", "норма прибыли", "доходность", а второй – "учетная ставка", "дисконт".
Итак, под процентными деньгами, или, кратко, процентами, в финансовых расчетах понимают абсолютную величину дохода от предоставления денег в долг в любой форме: в виде выдачи денежной ссуды, продажи в кредит, помещения денег на сберегательный счет, учет векселя, покупка сберегательного сертификата или облигации и т.д. В какой бы форме не выступали проценты, это всегда конкретное проявление такой экономической категории, как ссудный процент.
Очевидно, что обе ставки i и d взаимосвязаны, т.е., зная один показатель, можно рассчитать другой:
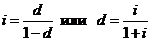 .
.
Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в формулах состоит в том, какая величина берется за базу сравнения: в формуле (1.1) – исходная сумма, в формуле (1.2) – возвращаемая сумма.
Как же соотносятся между собой эти показатели? Очевидно, что i>d, а степень расхождения зависит от уровня процентных ставок, имеющих место в конкретный момент времени. Так, если i=8%, то d=7,4%, т.е. расхождение сравнительно невелико; если i=80%, то d=44,4%, т.е. ставки существенно различаются по величине.
При заключении финансового или кредитного соглашения стороны (кредитор и заемщик) договариваются о размере процентной ставки – отношения суммы процентных денег (S-P), выплачиваемых за фиксированный отрезок времени, к величине ссуды. Интервал времени, к которому относится процентная ставка, называют периодом начисления. Ставка измеряется в процентах, в виде натуральной или десятичной дроби.
Начисление процентов, как правило, производится дискретно, т.е. в отдельные (обычно равноотстоящие) моменты времени (дискретные проценты), причем в качестве периодов начисления принимают год, полугодие, квартал, месяц. Иногда практикуется ежедневное начисление, а в ряде случаев удобно применять непрерывные проценты (см. пункт 2.4. Непрерывные проценты).
Проценты либо выплачиваются кредитору по мере их начисления, либо присоединяются к сумме долга. Процесс увеличения денег в связи с присоединением процентов к сумме долга называют наращением или ростомпервоначальной суммы.
В практике существуют различные способы начисления процентов, зависящие от условий контрактов. Соответственно применяют различные виды процентных ставок. Одно их основных отличий связано с выбором исходной базы (суммы) для начисления процентов. Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего срока ссуды или к сумме с начисленными в предыдущем периоде процентами. В первом случае процентные ставки называются простыми, во втором – сложными.
Процентные ставки, указываемые в контрактах, могут быть постоянными или переменными (“плавающими”). Плавающие ставки часто применяются во внешнеэкономических операциях. В этом случае значение ставки равно сумме некоторой базовой величины и надбавки к ней (маржи). Размер маржи определяется рядом условий (сроком операции и т.д.), он обычно находится в пределах 0,5–5%. Примером базовой ставки может служить лондонская межбанковская ставка ЛИБОР (LIBOR – London interbank offered rate) или московская межбанковская ставка МИБОР.
Рассмотрим методы анализа сделок, в которых предусматриваются разовые платежи при выдаче и погашении кредита или депозита. Задачи такого анализа сводятся к расчету наращенной суммы, суммы процентов и размера дисконта, современной величины (текущей стоимости) платежа, который будет произведен в будущем.
