Погашение долга переменными срочными уплатами
Далеко не всегда оказывается удобным условие Y=const.
Например погашение долга может быть связано с поступлением средств из каких-либо источников и зависеть от различных обстоятельств.
Срочные уплаты в этом случае образуют ряд, члены которого либо задаются заранее (график погашения), либо следуют какому – либо закону (прогрессии, заданной функцией).
Создание погасительного фонда
Если по условиям займа должник обязуется вернуть сумму долга в конце срока в виде разового платежа, то он должен предпринять для этого меры. При значительной сумме долга обычная мера заключается в создании погасительного фонда.
Погасительный фонд создается из последовательных взносов должника (например, на специальный счет в банке), на которые начисляются проценты. Сумма взносов в фонд вместе с начисленными процентами. Накопленная в погасительном фонде к концу срока, должна бать равна его сумме. Взносы могут быть как постоянными, так и переменными во времени.
Постоянные взносы в погасительный фонд
Необходимо определить размер срочных уплат и составляющих их элементов в зависимости от конкретных условий займов.
Пусть накопление производится путем регулярных ежегодных взносов R, на которые начисляются сложные проценты по ставке i одновременно происходит выплата процентов за долг по ставке r. Срочная уплата составит
Y=D*r+R
Обе составляющие срочной уплаты постоянны во времени.
Первая составляющая определяется величиной долга и процентной ставкой по займу.
Для нахождения второй составляющей пусть фонд должен быть накоплен за N лет. Тогда соответствующие взносы образуют постоянную ренту с параметрами R, N, I (пусть имеем дело с рентой постнумерандо)
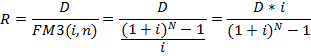
где FM3(i,N) – коэффициент наращения постоянного аннуитета со сроком N.
В целом срочная уплата находится по формуле:
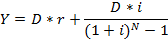
Если условия контракта предусматривают присоединение процентов к сумме основного долга, то срочная уплата определяется по формуле
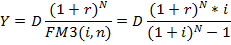
где (1+r)N – множитель наращения сложных процентов.
При создании погасительного фонда используется две процентные ставки – i (определяет темп роста погасительного фонда) и r (определяет сумму выплачиваемых за заем процентов).
Создание погасительного фонда выгодно должнику тогда, когда i>r, т.к. в этом случае должник на аккумулируемые в погасительном фонде средства получает больше процентов, чем сам выплачивает за заем.
Накопленные за t лет средства фонда определяются по формуле:
St-1=St(1+i)+Rt
Льготные займы и кредиты
В ряде случаев кредиты выдаются на льготных для заемщика условиях (под низкую процентную ставку).
Гранд – элемент – это условная потеря заимодавца, которая связана с применением более низкой процентной ставки, чем существующие ставки кредитного рынка.
Гранд элемент определяется в виде абсолютной или относительной величины.
Абсолютный гранд-элемент – рассчитывается как разность номинальной суммы займа и современной величины платежей по погашению займов, рассчитанный по рыночной ставке. В качестве ставки процента для расчета современной величины выбирают превалирующую на рынке долгосрочных кредитов ставку.
Размер абсолютного гранд элемента находится по формуле:
W=D-R
где D – сумма займа,
G – современная величина платежей, поступающих в счет погашения займа, рассчитанная по реальной ставке кредитного рынка.
Относительный гранд – элемент – характеризует отношение абсолютного гранд – элемента к сумме займа
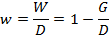
Выведем рабочие формулы для расчета W и w при условии, что долг и проценты выплачиваются в виде постоянных срочных уплат.
Пусть заем выдан на n лет и предусматривает выплату процентов по льготной ставке r. На денежном рынке аналогичные по сроку и величине займы выдаются по ставке i. В этом случае при отсутствии льготного периода срочная уплата составит:
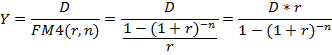
Современная величина всех выплат должника очевидно равна G=Y*FM4(i,n)
В итоге
W=D-G=D-Y*FM4(I,n)=D(1- 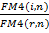 )
)
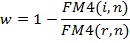
где FM4(i,n), FM4(r,n) - коэффициенты приведения постоянных годовых рент постнумерандо, определенные для процентных ставок i и r, i>r
наличие льготного периода увеличивает гранд – элемент.
Если в льготном периоде должник выплачивает проценты, то современная величина поступления по долгу определяется как сумма двух элементов – современных величин процентных платежей в льготном периоде и срочных уплат в оставшееся время.
Таким образом:
G=D*r*FM4(i,L) + Y*FM4(i, n-L)*vL
где n-L – продолжительность периода погашения задолженности,
L – продолжительность льготного периода.
Преобразуем формулу 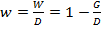
Современная стоимость поступлений по рыночной ставке i равна
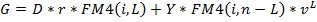
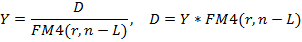
откуда
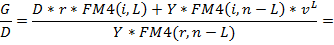
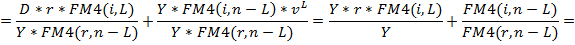
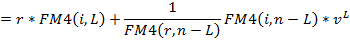
Таким образом:
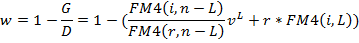
где FM4(i, n-L), FM4(r, n-L) – коэффициент приведения постоянных рент со сроком n-L и ставками i и r,
vL – дисконтный множитель по ставке i.
