Тема 1. Ведение. Финансовая математика (финансово – экономические расчеты)

Содержание

Тема 1. Ведение. Финансовая математика (финансово – экономические расчеты) 4

1.1. История развития и этапы становления науки «финансовая математика». Основополагающие взгляды и концепции, ведущие ученые и их труды.. 4

1.2. Сущность, функции и задачи финансовой математики на современном этапе. 8

Тема 2. Временная оценка денежных потоков. 11

2.1. Понятие денежного потока и его составляющие. 11

2.2. Виды денежных потоков. 11

2.3. Необходимость временной оценки денежных потоков. 12

2.4. Арифметическая и геометрическая прогрессия – последовательности чисел для анализа денежных потоков 13

Тема 3. Проценты, процентные деньги и процентные ставки. 15

3.1. Понятие процента, процентных денег и процентных ставок. 15

3.2. Простые проценты.. 16

3.2.1. Формула простых процентов. 16

3.2.2. Расчет процентов с использованием процентных чисел. 18

3.2.3. Переменные ставки. 19

3.2.4. Реинвестирование по простым ставкам.. 19

3.2.5. Определение срока ссуды и величины процентной ставки. 20

3.2.6. Дисконтирование по простым процентам.. 20

Тема 4. Функции сложного процента. 22

4.1. Функция №1 – будущая стоимость единицы.. 22

4.1.1. Формула сложных процентов. 22

4.1.2. Начисление процентов за дробное число лет. 23

4.1.3. Внутригодовые процентные начисления. 24

4.1.4. Номинальная и эффективная ставка процентов. 25

4.1.5. Переменная ставка сложных процентов. 26

4.1.6. Определение срока ссуды и величины процентной ставки. 27

4.1.7. Эквивалентность ставок и замена платежей. 27

4.1.8. Изменение финансовых условий. 27

4.1.9. Наращение по сложной учетной ставке. 28

4.2. Функция №2 – текущая стоимость единицы. Дисконтирование по сложной процентной ставке. 28

4.3. Функция №3 – текущая (приведенная) стоимость аннуитета (дисконтирование – обратная задача). 29

4.3.1. Определение текущей стоимости аннуитета. 29

4.3.2. Метод депозитной книжки. 34

4.3.3. Оценка аннуитета с изменяющейся величиной платежа (переменный аннуитет). 36

4.4. Функция №4 – периодический взнос на погашение кредита (взнос на амортизацию единицы). 38

4.5. Функция 5 – будущая стоимость аннуитета (наращение – прямая задача). 40

4.6. Функция №6 - периодический взнос в фонд накопления (фактор фонда возмещения). 45

4.7. Взаимосвязи между различными функциями. 45

Тема 5. Начисление процентов и налоги. 48

Тема 6. Валютные расчеты и проценты.. 50

6.1. Понятие национальной и иностранной валюты.. 50

6.2. Продажа валюты. Кассовые, форвардные и иные сделки. 51

6.3. Валютный арбитраж.. 55

Тема 7. Финансово – экономические расчеты при операциях с векселями. 57

7.1. Понятие векселя. Виды и сущность векселя. 57

7.3. Вексельный кредит: понятие, преимущества и недостатки. 59

7.3. Дисконтирование векселей по простой и сложной учетной ставке. 62

7.3.1. Дисконтирование векселей по простой учетной ставке. 62

7.3.3. Дисконтирование векселей по сложной учетной ставке. 63

Тема 8. Финансово – экономические расчеты при операциях с облигациями. 66

8.1.Основные определения и формулы.. 66

8.1.1. Понятие облигации. 66

8.1.2. Определение стоимости облигации. 67

8.1.3. Определение доходности облигаций. 69

8.1.3.1. Облигации без выплаты процентов (бескупонные или дисконтные облигации). 69

8.1.3.2. Облигации с выплатой процентов (купонные облигации). 70

Купонные облигации, выкупаемые по номиналу (облигации с периодической выплатой процентов и погашением номинала в конце срока). 70

Купонные облигации с периодической выплатой процентов и с выкупной ценой, отличающейся от номинала. 71

Купонные облигации с выплатой процентов и номинала в конце срока. 72

Тема 9. Финансово – экономические расчеты при операциях с акциями. 73

9.1. Основные определения. 73

9.2.Доходы от обыкновенных акций. 73

9.2.1. Метод капитализации дохода (модель дисконтирования дивидендов – модель Гордона). 73

9.2.2. Модель нулевого роста дивидендов. 76

9.2.3. Модель постоянного роста дивидендов. 76

9.2.4. Модель переменного роста (смешанная модель). 78

9.3. Доходы от привилегированных акций. 80

Тема 10. Инфляция. Учет инфляции в практике финансово – экономических расчетов. 82

10.1. Понятие, сущность и виды инфляции. 82

10.2. Индексы.. 82

10.3. Простые проценты и инфляция. 84

10.4. Сложные проценты и инфляция. 85

Тема 11. Финансово – экономические расчеты при предоставлении кредитов. 89

11.1. Разработка плана погашения долга и способы погашения задолженности. 89

11.1.1. Основные определения. 89

11.1.2. Разовое погашение кредита в конце срока. 89

11.1.3. Погашение основного долга (займа без процентов) равными долями. 90

11.1.3. Погашение долга равными срочными уплатами. 90

11.1.4. Погашение долга переменными срочными уплатами. 92

11.1.5. Создание погасительного фонда. 92

11.2. Льготные займы и кредиты.. 93

Тема 12. Финансово – экономические расчеты при лизинговых операциях. 95

12.1. Сущность и содержание лизинга. 95

12.2. Виды лизинговых сделок. 95

12.3. Способы, виды и состав лизингового платежа. 96

12.4. Порядок расчета величины лизингового платежа. 99

12.5. Выбор метода финансирования: покупка в собственность или лизинг. 103

Виды денежных потоков

Потки платежей могут быть регулярными (размеры платежей постоянные или следуют установленному правилу, предусматривающему равные интервалы между платежами) и нерегулярными.

Поток платежей, все члены которого являются положительными величинами, а временные интервалы между платежами одинаковы называется аннуитетом.

Аннуитет – частный случай денежного потока, в котором длительности всех периодов равны между собой. В качестве периода выступает любой промежуток времени.

Член аннуитета - любое денежное поступление.

Период аннуитета – величина постоянного временно интервала между двумя последовательными денежными поступлениями.

Если число равных временных интервалов ограничено, аннуитет называют срочным.

Срок аннуитета - интервал времени от начала первого периода аннуитета до конца последнего. Срок аннуитета можно определить, умножая его период на количество денежных поступлений.

Если в течение каждого базового периода начисления процентов денежные поступления происходят р раз, то аннуитет часто называют р-срочным. Часто в качестве такого базового периода выступает календарный год.

Типы аннуитетов:

Постнумерандо (или обычный аннуитет) – денежные поступления в конце периода аннуитета (например, регулярно поступающие платежи за пользование сданным в аренду участком в случае, если договором предусматривается регулярная оплата аренды по истечение определенного периода).

Пренумерандо (или авансовый аннуитет) - денежные поступления в начале периода аннуитета (например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления).

Если известно точное число членов аннуитета, то оно называется верным или безусловным.

Если количество членов аннуитета зависит от наступления некоторого события, то аннуитет называют условным (например пенсия, выплата которой прекращается после смерти пенсионера). Анализ условных аннуитетов – одна из основных задач страховой (актуарной) математики.

Переменный аннуитет - аннуитет, когда денежные поступления по периодам варьируется.

По числу раз начислений процентов по протяжении года различают:

· аннуитеты с ежегодным начислением;

· аннуитеты с начислением m раз в году;

· аннуитеты с непрерывным начислением.

Моменты начисления процентов необязательно совпадают с моментами выплат членов аннуитета. Однако расчеты заметно упрощаются, если момент начисления процентов и момент выплаты совпадают.

По количеству членов различают:

· аннуитеты с конечным числом членов или ограниченные аннуитеты (их срок заранее оговорен);

· бесконечные (вечные) аннуитеты – встречаются на практике в ряде долгосрочных операций, когда предполагается, что период функционирования анализируемой системы или срок операции весьма продолжителен и не оговаривается конкретными датами (например, выплаты процентов по бессрочным облигационным займам).

Рента – регулярный равновеликий доход, получаемый с капитала или земли, не требующий от получателя предпринимательской деятельности.

Финансовая рента – серия периодически осуществляемых платежей:

По величине своих членов ренты делятся на:

· постоянные (с одинаковыми размерами члена ренты);

· переменные (их члены изменяют свои размеры во времени, следуя какому – либо закону, например, арифметической или геометрической прогрессии, или несистематично (задаются таблицей)).

Простые проценты

Формула простых процентов

Процесс наращения – это процесс определения денежной суммы в будущем, исходя из заданной суммы сейчас.

Экономический смысл операции наращения – определении величины той суммы, которой будет располагать или желает располагать инвестор по окончании операции наращения.

При предоставлении денег в долг их владелец получает доход в виде процентов. При этом выделяется некоторый основной интервал времени, который называется базовым. На практике в качестве базового интервала часто берется год (стандартный временной интервал в финансовых вычислениях) и процентная ставка устанавливается в виде годовой ставки. Подразумевающей однократное начисление процентов по истечение года после получения ссуды.

PV – сегодняшняя стоимость денег;

FV - будущая стоимость сегодняшней суммы денег (PV);

r – ставка процентов (в десятичных дробях);

n – число лет на которое выдана ссуда.

PV

FV

n

t (время)

Сумма начисленных процентов (абсолютный прирост денег) (I) за 1 год:

I=FV-PV

Сумма начисленных процентов за ряд лет n (произведение абсолютных приростов на количество лет ссуды)

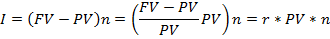
где 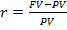– ставка процентов.

Т.о. размер ожидаемого дохода зависит от трех факторов:

- величина инвестированной суммы (PV),

-уровень процентной ставки (r),

- срок финансовой операции (n).

Определение наращенной суммы по схеме простых процентов (формула простых процентов)

FV=PV+I=PV+PV*r*n=PV(1+r*n)=PV*k_n,

где k_n = 1+r*n – множитель (коэффициент) наращения простых процентов.

К простым процентам прибегают в случаях:

- выдачи краткосрочных ссуд, т.е. ссуд, срок которых либо равен году, либо меньше его, с однократным начислением процентов;

- когда проценты не присоединяются к сумме долга, а периодически выплачиваются.

Формула простых процентов для случая, если срок ссуды (n) выражается в месяцах (М):

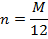
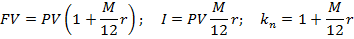
Формула простых процентов для случая, если срок ссуды (n) выражается в днях (t)

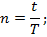
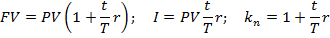
где t – число дней ссуды, т.е. продолжительность срока, на который выдана ссуда;

Т – расчетное число дней в году (временная база).

Временную базу (Т) можно представить по разному:

- как условно состоящую из 360 дней. В этом случае речь идет об обыкновенном или коммерческом проценте;

- как состоящую из действительного числа дней в году (365 или 366). В этом случае получают точный процент.

Определение числа дней ссуды (t):

- приближенное число дней ссуды получают тогда, когда исходят из того, что продолжительность любого месяца составляет 30 дней;

- точное число дней ссуды получают тогда, когда рассчитывают фактическое число дней между датой выдачи ссуды и датой возврата ссуды с использованием прямого счета или специальных таблиц порядковых номеров дней года.

Т.о. если время финансовой операции выражено в днях, то расчет простых процентов может быть произведен одним из трех способов:

1. Германская практика расчета (Германия, Дания, Швеция) – обыкновенные проценты (продолжительность года принимается равной 360 дням) с приближенным числом дней ссуды (продолжительность целого месяца принимается равной 30 дням( (360/360)

2. Французская практика расчета (Франция, Бельгия, Испания, Швейцария) - обыкновенные проценты (--//-- 360 дней) с точным числом дней ссуды (продолжительность ссуды рассчитывается точно по календарю) (360/365)

3. Английская практика расчета (Англия, США. Португалия) – продолжительность года и продолжительность ссуды берутся точно по календарю (365/365)

В зависимости от использоваия конкретной практики начисления простых процентов их сумма будет различаться по абсолютной величине. Результат финансовой операции зависит т выбора способа начисления простых процентов. Проценты с точным числом дней ссуды обычно получаются выше процентов с приближенным числом дней ссуды.

Учетная ставка процента определяется по формуле:

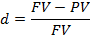
Ставка процента и учетная ставка взаимосвязаны, т.е. зная один показатель можно рассчитать другой.

Вывод формул:

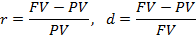
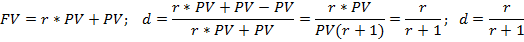
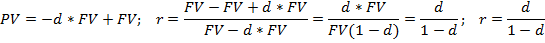
Дисконт фактор показывает какую часть сумма PV составляет в сумме FV.

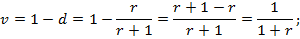
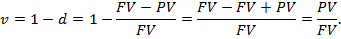
Индекс роста В суммы PV за время t

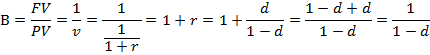
Индекс роста показывает во сколько раз увеличилась первоначальная сумма за время t.

Индекс роста за время t = t₁ + t₂ + t₃ +…+t_n равен:

В=В₁*В₂*В₃*…В_n.

При n=1 FV=PV(1+r),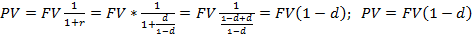

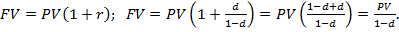
Т.о. FV=PV(1+r), PV=FV(1-d),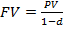

Переменные ставки

В своей практике банки зачастую изменяют процентные ставки. При переменной процентной ставке наращенная сумма FV определяется по формуле:

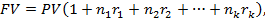
где k – количество периодов начисления;

n_k – продолжительность k-го периода, дней n=t/T,

r_k – ставка процентов в k-ом периоде, доли ед.

Формула сложных процентов

Применение схемы сложных процентов целесообразно тогда, когда проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга.

Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процента.

Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов и последующее начисление процентов происходит на увеличенную сумму долга.

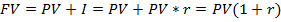– за один период начисления,

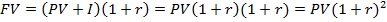– за два периода начисления.

(подставляем вместо I=PV*r)

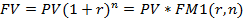- за n периодов начисления.

где FV - наращенная сумма долга,

PV – первоначальная сумма долга,

r - ставка процентов в периоде начисления,

n - количество периодов начисления,

FM1(r,n)=(1+r)ⁿ – множитель наращения сложных процентов (будущая стоимость единицы).

Сложные проценты отличаются от простых базой начисления.

Простые проценты начисляются все время на одну и ту же первоначальную сумму, т.е. база начисления является постоянной величиной.

Сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу.

Коэффициенты (множители) наращения зависят от процентной ставки и числа периодов наращения. Их можно определить по специальным таблицам.

Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (рубль, доллар, пр.) через n периодов при заданной процентной ставке r.

Сложные проценты

Простые проценты

FV

t

Рис. Наращение по простым и сложным процентам

Из рис. видно, что при краткосрочных ссудах (n<1) начисление по простым процентам предпочтительнее, чем по сложным процентам. При сроке ссуды в 1 год разница отсутствует. При среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам выше, чем по простым.

При любом r:

Если 0<n<1, то (1+nr)>(1+r)ⁿ

Если n=1, то (1+nr)=(1+r)ⁿ

Если n>1, то (1+nr)<(1+r)ⁿ

Финансовое соглашение может предусматривать плавающие процентные ставки

Пусть n₁, n₂, …, n_m следующие друг за другом периоды. На период n_k установлена процентная ставка r_k.

При капитализации процентов наращенная сумма за время определяется по формуле:

Метод депозитной книжки

Суть метода. Сумма, положенная на депозит, приносит доход в виде процентов. При снятии с депозита некоторой суммы базовая величина, с которой начисляются проценты, уменьшается. Эта ситуация и имеет место в случае с аннуитетом.

Текущая стоимость аннуитета – это величина депозита с общей суммой причитающихся процентов, ежегодно уменьшающаяся на равные суммы.

Эта сумма годового платежа включает в себя начисленные за очередной период проценты, а также некоторую часть основной суммы долга. Таким образом, погашение исходного долга осуществляется постепенно в течение всего срока действия аннуитета.

Структура годового платежа постоянно меняется: в начальные периоды в нем преобладают начисленные за очередной период проценты. С течением времени доля процентных платежей постоянно уменьшается и повышается доля погашаемой части основного долга.

Интерпретация приведенной стоимости аннуитета с помощью метода депозитной книжки.

Пусть получена ссуда в сумме D₁=S на n лет под процентную ставку r. Сложные проценты начисляются на непогашенный остаток.

Определяем величину годового платежа при возврате долга равными суммами в конце каждого года.

Пусть А – годовой платеж.

В конце первого года часть годового платежа I₁=S*r идет на уплату процентов.

Оставшаяся часть H₁=A-S*r – идет на уплату части долга.

Таким образом на начало второго года величина непогашенного остатка:

D₂=S-(A-S*r)=S(1+r)-A=D₁(1+r)-A.

Аналогично остаток долга на начало k-го года связан остатком долга на начало предыдущего года следующим соотношением:

D_k=D_k-1(1+r)-A, (*)

Из этой формулы:

А=D_k-1*r + (D_k-1 – D_k) – годовой платеж.

где D_k-1*r - проценты, начисляемые на текущий долг,

D_k-1-D_k – сумма, идущая на погашение основного долга.

Если D₁=S, D₂=S(1+r)-A, то

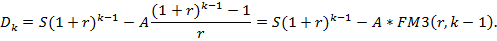
Т.к. долг должен быть выплачен через n лет, то D_n-1=0, т.е. справедливо равенство (k=n+1):

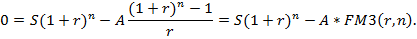
Из этого равенства следует:

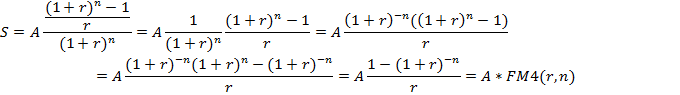
Следовательно S- приведенная стоимость постоянного аннуитета постнумерандо с членом, равным А, т.е.:

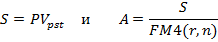
I_k=D_k*r – величина процентов за k-й год.

Умножая обе части (*) на r получим:

D_k*r=D_k-1(1+r)r-A*r,

т.е.I_k=I_k-1(1+r)-A*r (**)

Н_k=A-I_k – погашенная часть долга в k-м платеже.

Согласно (**) H_k=A-I_k-1(1+r)+A*r=(A-I_k-1)(1+r).

Таким образом

Н_k=H_k-1(1+r)

Из последней формулы видно, что суммы, идущие на погашение основного долга увеличиваются.

Валютный арбитраж

Валютный арбитраж - покупка (продажа) валюты с последующим совершением контрсделки (обратной сделки) для получения курсовой прибыли.

Виды валютного арбитража:

Пространтсвенный арбитраж – используется для получения прибыли за счет разницы курсов на различных валютных рынках.

Временной арбитраж – используется для получения прибыли за счетизменения курса в течение определенного времени.

Валютный арбитраж связан с открытием спекулятивной валютной позиции.

Валютная позиция банка определяется соотношением его требований и обязательств в соответствующих валютах.

В случае если требования и обязательства банка равны между собой валютная позиция будет закрытой.

В случае если требования и обязательства банка не совпадают валютная позиция будет открытой.

Виды открытых валютных позиций:

Короткая позиция - при которой сумма обязательств в валюте превышает сумму требований (обозначается знаком «-»).

Длинная позиция - возникает в том случае, когда сумма требований в иностранной валюте превышает сумму обязательств (обозначается знаком «+»).

Короткая позиция закрывается путем покупки ранее проданной валюты. Закрытие позиции при снижении курса приводит к получению курсовой прибыли. Следовательно, короткую позицию следует открывать, если ожидается понижение курса валюты.

Длинная позиция закрывается путем продажи ранее купленной валюты. Поэтому при длинной позиции возникает риск убытка от понижения курса, в то время как при повышении курса банк получит прибыль.

Процентным арбитражем на денежных рынках называется перемещение ресурсов от одной валюты к другой ради улучшения условий кредитования и заимствования.

Фактически процентный арбитраж сводится к выбору страны или валюты с наиболее благоприятной процентной ставкой кредита. В качестве финансовых инструментов при процентном арбитраже могут фигурировать срочные банковские депозиты. Перемещение ресурсов из одной валюты в другую предполагает наличие валютного риска.

Понятие облигации

Под облигацией понимается ценная бумага, свидетельствующая о том, что ее держатель предоставил заем эмитенту этой бумаги.

Фундаментальные свойства облигаций:

1. Наличие конечного срока действия облигации. При выпуске облигаций эмитент в проспекте эмиссии указывает срок погашении облигации, при наступлении которого предприятие выкупает свои облигации у инвесторов, выплачивая им номинальную стоимость облигации.

2. Владельцы облигации, как кредиторы, имеют приоритет в получении дохода:

- выплаты в пределах установленного норматива являются частью издержек предприятия и включаются в себестоимость (по облигациям эмитент даже при отсутствии прибыли обязан выплачивать доход);

- выплаты по облигациям являются обязанностью эмитента, которую он принял на себя, выпустив облигации в обращение (выплаты дивидендов по акциям не является жестким обязательством эмитента, по облигациям выплата процентов является обязательной);

3. Наличие у владельцев облигаций права на первоочередное удовлетворение их требований по сравнению с акционерами при ликвидации предприятия. Владельцы облигаций являются кредиторами. Поэтому в случае ликвидации предприятия им будет погашена вся задолженность по текущим платежам за истекший период и выплачена номинальная стоимость облигации. Расчеты же с акционерами производятся после погашения задолженности перед всеми кредиторами.

Основные параметры облигации:

- номинальная цена (номинал);

- выкупная цена или правило ее определения если она отличается от номинала;

- дата погашения;

- норма доходности или купонная процентная ставка;

- даты выплат процентов.

Виды облигаций:

1. По методу обеспечения:

Закладные (обеспеченные) облигации – выпускаются под залог конкретного имущества:

- ипотечные облигации (выпущены под залог земли или недвижимости);

- облигации с переменным (плавающим) залогом (в качестве обеспечения выступают машины, оборудование, материалы, стоимость которых подвержена колебаниям во времени);

- облигации под залог ценных бумаг.

Бесзакладные (необеспеченные) облигации – это прямые долговые обязательства компании, которые не обеспечены никаким залогом.

2. По способу получения дохода:

Купонные облигации – облигации, к которым прилагаются купоны с указанием на них процента доходности и даты выплаты дохода (облигации с фиксированным и плавающим купоном)

Дисконтные – облигации, по которым проценты не выплачиваются, а владелец облигации получает доход за счет того, что облигация продается с дисконтом, т.е. по цене ниже номинала. Выкуп облигации осуществляется по номинальной стоимости за счет чего их владельцы получают соответствующий доход.

3. Индексируемые облигации – выпускаются с целью защиты инвестора от обесценения облигаций в связи с инфляцией, изменением валютного курса и т.д. Отличительной чертой индексируемых облигаций является то, что сумма выплат по купону и номинальная стоимость облигаций корректируется на специальный коэффициент, отражающий изменение соответствующего показателя (темп инфляции, динамика валютного курса и т.д.)

Индексы

Измерение уровня инфляции

Базовыми показателями, которые используют для измерения уровня инфляции, служат индексы цен.

Виды индексов цен.

1. Индексы оптовых цен – показывают изменения среднего уровня цен реализации продукции промышленных, торговых и сельскохозяйственных предприятий (но не оптовой торговли);

2. Индексы розничных цен – рассчитывают либо как совокупный индекс цен на продукцию, продаваемую в розничной торговле, либо только по корзине специально значимых товаров. Второй из этих индексов означает «стоимость жизни» в стране особенно важен ля населения.

3. Дефлятор ВНП – определяется по объему конечной продукции, которая формирует стоимость ВНП, в том числе по ценам на важнейшие товары, покупаемые населением, оборудование и другие основные средства, покупаемые фирмами, тарифам на услуги, оказываемые государственному сектору, а также внешнеторговым ценам. Исключаются только цены на промежуточные продукты, которые служат в качестве оборотных средств. Эти индексы являются важнейшими показателями, т.к. отражают действительный уровень инфляции в стране.

Наиболее известные для расчета индекса цен формулы:

1. Формула Ласпейреса

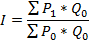
2. Формула Пааше

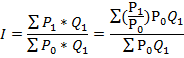
3. Формула Фишера

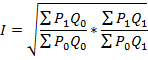
где Р₁ и Р₀ – цены текущего и базисного периодов;

Q₁ и Q_{2 –} количество продукции в текущий и базисный периоды.

Пусть выбран определенный набор товаров и услуг и пусть за время t его стоимость изменилась от суммы Р₁ до суммы Р₂.

Пусть индекс цен будет выражаться формулой:

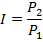
Темпом инфляции за время t называется величина

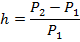
Темп инфляции (умноженный на 100) показывает, на сколько процентов выросли цены за период времени t.

Соотношение между индексом цен и темпом инфляции:

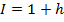
Например, если I=2,4, то h=1,4, т.е. цены за рассматриваемый период выросли в 2,4 раза, или, что эквивалентно, на 140%.

Индекс цен за данный период показывает, во сколько раз выросли цены по отношению к уровню цен предыдущего года.

Если известны индексы цен 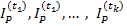(или темпы инфляции 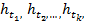) за периоды времени t₁, t₂, …, t_k и эти периоды расположены последовательно друг за лругом, то индекс цен за время t = t₁+t₂+…+t_k будет равен

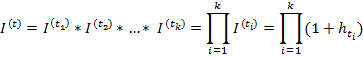
Знак 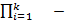обозначается умножение.

Если за время t была получена некоторая наращенная сумма FV, а индекс цен составил величину I^(t), то эта сумма с учетом ее обесценения составит:

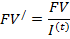
Например при годовой инфляции 20% сумма в 3 тыс. руб. через год по своей покупательной способности в ценах текущего дня (т.к. t=1, h₁=0,2, I=1,2) составит величину

Простые проценты и инфляция

Пусть на капитал PV происходит начисление простых процентов по ставке r в течение времени n и индекс цен за это врем равен I⁽ⁿ⁾, тогда, учитывая обесценение денег за это время получим:

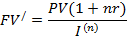
где 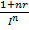– множитель наращения простых процентом инфляции.

Из формулы следует, что реальное наращение первоначального капитала с учетом покупательной способности денег будет только в том случае, если 1+nr>I⁽ⁿ⁾

Если 1+nr=I⁽ⁿ⁾ , то наращение только компенсирует действие инфляции

Из равенства 1+nr=I⁽ⁿ⁾ найдем r

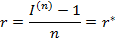
где r^* - минимально допустимая процентная ставка, при которой не происходит реального уменьшения капитала (эрозии капитала).

Ставка, превышающая r* называется положительной процентной ставкой, т.к. только при ее применении будет происходить реальное увеличение капитала.

Брутто – ставка (r^/) – ставка процентов, индексированная с учетом роста уровня цен для учета инфляции

Для обеспечения полной компенсации негативного воздействия инфляции и получения доходности согласно первоначальной ставке r, размер брутто – ставки r^/ определяется из равенства

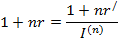
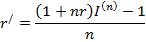
Если задана брутто – ставка r^/ (т.е. объявлена норма доходности), то можно определить реальную процентную ставку, т.е. доходность с учетом инфляции при начислении простых процентов

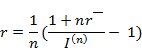
Т.о. при инфляции различают следующие виды процентных ставок

Номинальная процентная ставка – это исходная базовая (как правило годовая) процентная ставка, указанная в договорах. Доходность, выражаемая этой ставкой, не скорректирована на инфляцию.

Реальная процентная ставка - показывает доходность с учетом инфляции, характеризующейся снижением покупательной способности денег. В условиях инфляции она всегда меньше номинальной процентной ставки и может быть даже отрицательной.

Положительная процентная ставка - это любая ставка, при которой будет происходить реальное увеличение стоимости капитала при данном индексе инфляции.

Брутто – ставка процента – ставка процента, индексированная с учетом роста уровня цен для учет инфляции (ставка при которой капитал действительно растет с необходимой доходностью) .

В условиях галопирующей инфляции (15-20% в год) используется и плавающая процентная ставка.

При начислении процентов на вклады и кредиты сроком до года применяется формула 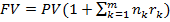, которую можно записать в виде:

где t_k – продолжительность в днях периода, на который установлена процентная ставка r_k,

Т - количество дней в году.

Величина учетной ставки d^/, компенсирующей инфляционные потери, определяется из равенства:

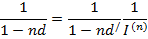
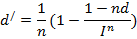
Если задана ставка d^/ , то из последнего равенства можно определить реальную учетную ставку, позволяющую оценить соответствующим образом доходность при инфляции

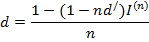
Если индекс цен меньше единицы, то это свидетельствует о дефляции.

Сложные проценты и инфляция

Пусть на капитал PV в течение n лет начисляются сложные проценты и индекс цен за это время равен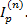

FV=PV*cⁿ, 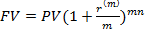= PV*cⁿ.

где m - количество начислений в год.

Но с учетом инфляции:

(*)

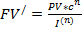Отсюда ясно, что для того, чтобы не происходило эрозии капитала должно выполняться неравенство сⁿ≥I⁽ⁿ⁾, что равносильно неравенству

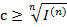
причем если , то наращение капитала лишь нейтрализует действие инфляции.

Ставка, для которой соответствующий коэффициент с превышает с^*, называется положительной ставкой.

Например, если 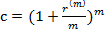, то положительная процентная ставка определяется из неравенства , откуда следует

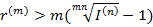
Если в течение n лет ожидаемый ежегодный индекс инфляции равен I, то I=1+h, I⁽ⁿ⁾=(I)ⁿ=(1+h)ⁿ, где h – ожидаемый ежегодный темп инфляции.

Тогда .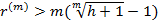

Если сложные проценты начисляются один раз в год, то должно быть r^(m)=r>h, т.е. процентная ставка должна превышать темп инфляции.

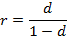
Полагая, что , находим, что положительная учетная ставка удовлетворяет неравенству 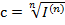, , 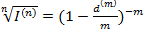, 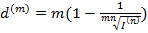а при m=1 и I⁽ⁿ⁾=(1+h)ⁿ получим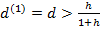

Для обеспечения реального роста стоимости первоначального капитала необходимо исходную ставку увеличивать (индексировать). Выбор величины такой индексированной ставки, называемой брутто-ставкой, определяется поставленными целями.

Для обеспечения реальной доходности согласно коэффициенту наращения с необходимо так индексировать исходную ставку (увеличивать на инфляционную премию), чтобы новый коэффициент наращения с^/ полностью компенсировал потери из-за инфляции. Т.о., с^/ определяется из равенства:

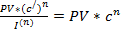, Þ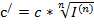

Размер брутто – ставки (r^/) обеспечивает полную компенсацию негативного воздействия инфляции и получение доходности. Следовательно в формуле (*) множитель сⁿ нужно приравнять к множителю , тогда если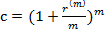

,

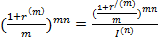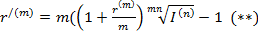– брутто ставка наращения

Задавая брутто- ставки в формуле (**) можно определить реальную ставку наращения r^(m) (выразим из (**) r^(m))

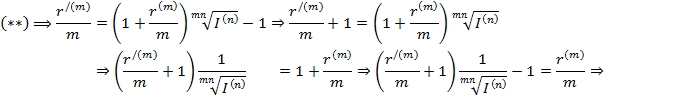
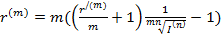- реальная ставка наращения

Выводим формулы для определения реальной брутто – ставки d^/(m) и реальной учетной ставки d^(m)

Если , то с учетом (*)