Алгоритм метода имитации Монте-Карло

Шаг 1. Опираясь на использование статистического пакета, случайным образом выбираем, основываясь на вероятностной функции распределения значение переменной, которая является одним из параметров определения потока наличности.

Шаг 2. Выбранное значение случайной величины наряду со значениями переменных, которые являются экзогенными переменными используется при подсчете чистой приведенной стоимости проекта.

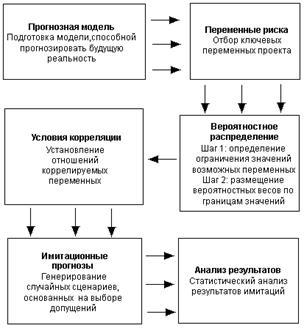
Рис. 4.3.1 Построение модели методом Монте-Карло [11]

Шаги 1 и 2 повторяются большое количество раз, например, 1000, и полученные 1000 значений чистой приведенной стоимости проекта используются для построения плотности распределения величины чистой приведенной стоимости со своим собственным математическим ожиданием и стандартным отклонением.

Используя значения математического ожидания и стандартного отклонения, можно вычислить коэффициент вариации чистой приведенной стоимости проекта и затем оценить индивидуальный риск проекта, как и в анализе методом сценариев.

Применение метода имитации Монте-Карло требует использования специальных математических пакетов, в то время, как метод сценариев может быть реализован даже при помощи обыкновенного калькулятора.

Анализ рисков с использованием метода имитационного моделирования Монте-Карло представляет собой “воссоединение” методов анализа чувствительности и анализа сценариев на базе теории вероятностей.

Итогом такого комплексного анализа выступает распределение вероятностей возможных результатов проекта.

Задание

Используйте придуманную вами задачу разработки управленческого решения. Задайтесь параметром, который может рассматриваться в условиях риска, и решите ее методом Монте-Карло.

Порядок выполнения работы

1. Задайтесь параметром, который может рассматриваться в условиях риска. Это может быть тот же самый параметр или какой-либо другой. Согласуйте с преподавателем выбранный вами параметр.

2. Задайтесь законом распределения случайного параметра.

3. Получите выборку значений этого параметра и определите на ее основе параметры функции распределения.

4. Запустите датчик псевдослучайных чисел и сгенерируйте выборку объемом не менее 10000 значений.

5. Постройте гистограмму распределения случайных чисел от датчика.

6. Рассчитайте средние значения карманов распределения

7. Подставьте средние значение карманов гистограммы в качестве параметра и решите задачу оптимизации, определяя при этом решение и значение критериальной функции.

8. Замените на построенной ранее гистограмме значения на оси абсцисс на значения критериальной функции и постройте график функции распределения целевой функции (интегральное представление).

9. Выберите оптимальное решение, соответствующее максимуму среднего значения критериальной функции (М‑постановка) или заданному значению вероятности (Р‑постановка).

Контрольные вопросы

1. В чем суть анализа влияния факторов финансового риска при помощи метода Монте-Карло?

2. Каковы преимущества метода Монте-Карло?

3. Что позволяет получить использование метода Монте-Карло при оценке проектных и финансовых рисков?

4. На чем основано построение модели реализации проекта методом Монте-Карло?

Лабораторная 4.4. Освоение различных методик оценки финансовых рисков по инвестиционному проекту с помощью средств MS EXCEL

Цель работы 4.4. – приобрести навыки использования методов оценки финансовых рисков инвестиционных проектов с помощью средств MS EXCEL.

Теоретическое основание

В настоящее время в теории и практике хозяйствования одним из направлений оценки эффективности инвестиционных проектов в условиях нестабильной внешней среды является метод сценариев. Данный метод предполагает прогнозирование вариантов развития внешней среды и расчет оценок эффективности инвестиций для каждого сценария. Если сценариям приписываются определенные вероятности, то можно построить профиль риска, оценить стандартное отклонение и асимметрию распределения. Часто разрабатывают так называемые "пессимистический", "наиболее вероятный" и "оптимистический" сценарии, позволяющие приближенно оценить разброс результатов проекта и его прибыльность (убыточность) при ухудшении экономической ситуации [13].

Метод сценариев позволяет совместить исследование чувствительности результирующего показателя с анализом вероятностных оценок его отклонений. Процедура использования данного метода в процессе анализа инвестиционных рисков включает следующие действия:

1. Определяется несколько вариантов изменений ключевых исходных показателей.

2. Каждому варианту изменений приписывается его вероятностная оценка.

3. Для каждого варианта рассчитывается вероятное значение критерия NPV, а также оценки его отклонений от среднего значения.

4. Проводится анализ вероятностных распределений полученных результатов.

Проект с наименьшим стандартным отклонением и коэффициентом вариации считается менее рисковым.

Пример 1

Предположим, что по результатам анализа проекта из предыдущего примера были составлены следующие сценарии его развития и определены возможные вероятности их осуществления (см. таблицу 3). Необходимо провести анализ риска проекта.

Таблица 4.4.1.

Сценарии реализации проекта по производству продукта «А»

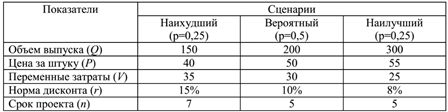
Решение с помощью Excel:

Для формирования первого сценария выполним следующие действия:

1. Выделим в листе Анализ чувствительности (рисунок 1) блок ячеек В2:В6.

2. Выберем в главном меню Сервис пункт Сценарии. В появившемся диалоговом окне Диспетчер сценариев зададим операцию Добавить. Результатом указанных действий будет появление окна Добавление сценария.

3. Введем имя сценария Вероятный. В поле Изменяемые ячейки содержатся координаты входного блока В2:В6.

4. После нажатия кнопки [ОК] на экране появится диалоговое окно Значения ячеек сценария, содержащие данные выделенного ранее блока, которые не будем изменять. Выполним нажатие кнопки [ОК].

Таким образом, будет сформирован «Вероятный» сценарий (см. рисунок 4.4.1.).

Рисунок 4.4.1. – Диалоговое окно Значения ячеек сценария «Вероятный»

Чтобы сформировать следующий сценарий («наилучший» или «наихудший» в соответствии с данными таблицы 4.4.1.), выберем в Диспетчере сценариев кнопку Добавить и повторим действия 2-4. Завершив формирование сценариев, выберем Отчет, укажем требуемый пункт Структура, нажмем кнопку [ОК] (рисунок 4.4.2.).

В результате Excel автоматически сформирует отчет на отдельном листе рабочей книги и присвоит ему имя Структура сценария.

Далее выполним ряд несложных преобразований, которые должны содержаться в листе Структура сценария (рисунок 4.4.3.). Во-первых, удалим ненужные строки и столбцы.

Во-вторых, добавим строку Вероятности.

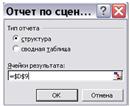
Рисунок 4.4.2. – Диалоговое окно Отчет по сценарию

Далее проведем вероятностный анализ риска инвестиционного проекта.

Присвоим ячейке В13 собственное имя Среднее и введем следующую формулу:

=СУММПРОИЗВ(B4:D4;B11:D11) Результат: 10496.

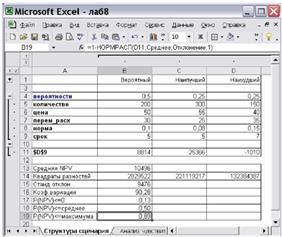
Рисунок 4.4.3. – С помощью листа Структура сценария можно проводить вероятностный анализ риска инвестиционного проекта

Для вычисления стандартного отклонения необходимо предварительно найти квадраты разностей между средней ожидаемой NPV и множеством ее полученных значений.

Поэтому в ячейку В14 введем формулу, которую скопируем в ячейки С14:D14

=(B11-Среднее)^2 Результат: 2829522.

Присвоим ячейке В15 собственное имя Отклонение и введем следующую формулу:

=КОРЕНЬ(СУММПРОИЗВ(B14:D14;B4:D4)) Результат: 9476.

В ячейку В16 введем формулу для расчета коэффициента вариации:

=Отклонение/Среднее*100 Результат: 90,28.

Таким образом, исходя из предположения о нормальном распределении случайной величины, с вероятностью около 70% можно утверждать, что значение NPV будет находиться в диапазоне 10496±9476 (одна «сигма»). Определим вероятность того, что значение

NPV будет:

1) меньше либо равно нулю;

2) меньше либо равно среднему значению;

3) меньше максимального значения.

Для этого в ячейки В17, В18 и В19 введем соответственно формулы:

=НОРМРАСП(0;Среднее;Отклонение;1) Результат: 0,13.

=НОРМРАСП(Среднее;Среднее;Отклонение;1) Результат: 0,50.

=1-НОРМРАСП(D11;Среднее;Отклонение;1) Результат: 0,89.

Данные результаты говорят о том, что при соблюдении требований закона нормального распределения, величина NPV в 13 случаях из 100 будут меньше нуля, в половине случаев – меньше среднего значения и в 89 случаях меньше максимального значения, полученного по наиболее благоприятному сценарию.

Как видно из полученного отчета, критерий NPV при наиболее неблагоприятном развитии событий будет отрицательным (-1010 руб.). Полученные результаты в целом свидетельствуют о наличии риска для этого проекта. Среднее значение NPV (10496) превышает как прогноз экспертов (8814), так и величину стандартного отклонения (9476).

Значение коэффициента вариации (90%) близко к 100%, следовательно, собственный риск данного проекта следует признать значительным. Но в том случае, если значения стандартного отклонения и коэффициента вариации по этому проекту меньше, чем у остальных альтернатив, при прочих равных обстоятельствах ему следует отдать предпочтение.

В целом метод сценариев позволяет получить достаточно наглядную картину результатов для различных вариантов реализации проектов. Он обеспечивает информацией, как о чувствительности, так и возможных отклонениях выбранного критерия эффективности.

Задания для самостоятельного решения

1. Используя данные из примера, рассмотренного в лабораторной работе 4.4., проведите анализ чувствительности критерия NPV в зависимости от изменения: 1) цены изделия и переменных затрат с шагом 5 ден. ед. за штуку; 2) нормы дисконта с шагом 1%; 3) срока проекта с шагом 1 год.

2. Фирма «X» рассматривает проект по выпуску продукта «П» со следующими исходными данными:

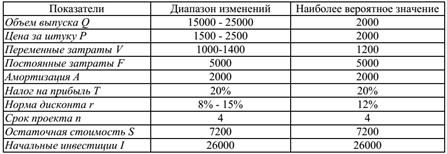
Определите:

а) критерии NPV, IRR, PI при наиболее вероятных значениях ключевых параметров;

б) то же при наименее благоприятных значениях ключевых параметров.

Проведите анализ чувствительности NPV проекта к изменениям ключевых переменных с шагом 10%. Изменение какого параметра оказывает наиболее сильное влияние на NPV проекта?

3. Используя данные и результаты анализа предыдущего задания, проведите графический анализ безубыточного объема выпуска продукта «П».

4. Инвестиционная компания обратилась к вам c просьбой провести оценку риска проекта со следующими сценариями развития.

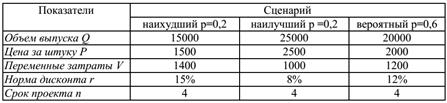
Остальные данные возьмите из задания 2.

Определите:

а) критерии NPV, IRR, PI для каждого сценария;

б) ожидаемые значения критериев эффективности.

Проведите:

а) анализ вероятностных распределений критерия NPV;

б) оценку собственного риска проекта.

Контрольные вопросы

1. Что предполагает метод сценариев при осуществлении оценки проектных и финансовых рисков?

2. Какие возможности открывает для предпринимателя использование метода сценариев при оценке проектных и финансовых рисков?

3. Какова последовательность действий при осуществлении оценки проектных и финансовых рисков методом сценариев?

Лабораторная работа №5 (2 часа)

ФИНАНСИРОВАНИЕ РИСКОВ

Лабораторная работа 5. Разработка плана погашения кредита

Цель работы 5 – приобрести навыки составления плана погашения кредита с помощью MS EXCEL.

Теоретическое основание

Разработка планов погашения кредитов – одна из важнейших и часто встречающихся на практике задач. Как правило, кредит погашается одинаковыми платежами, равномерно распределенными во времени. Такой метод погашения часто называется амортизацией долга. Возникающие при этом денежные потоки представляют собой аннуитет. Основная задача планирования поступлений (выплат) по кредитам сводится к исчислению составных элементов платежей и распределению их во времени. Возможные стратегии погашения кредита в условиях денежного дефицита представлены на рисунке 5.1.

Рисунок 5.1. Оплата кредиторской задолженности за товары, работы, услуги в условиях денежного дефицита [14]

Кроме этого, необходимопоследовательно отсортировать кредиторскую задолженность по таким признакам:

1) по срокам оплаты (сначала просроченная);

2) по риску инициирования банкротства (сначала с высоким риском, потом с меньшим);

3) по уровню штрафных санкций (сначала с высокими, затем с низкими);

4) по плановым срокам оплаты (чем раньше дата оплаты, тем выше выдается в сортировке);

5) по убыванию суммы кредиторской задолженности (логика в том, что чем выше сумма задолженности, тем выше риск инициирования банкротства, соблазн перепродать долг или подать в суд, то есть истребовать в судебном порядке штрафные санкции, плюс риск судебных издержек).

Для повышения эффективности плана погашения кредита следует:

· решить вопрос о целесообразности работы с поставщиками;

· мотивировать сотрудников для более эффективной работы с кредиторской задолженностью;

· выявить и устранить причины неэффективного управления кредиторской задолженностью;

· определить оптимальную структуру кредиторской задолженности для конкретного предприятия и в конкретной ситуации;

· проанализировать соответствие фактических показателей их рамочному уровню, а также причины возникших отклонений;

· разработать и провести комплекс практических мероприятий по приведению структуры долгов в соответствие с плановыми (оптимальными) параметрами.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Сформируем шаблон для разработки планов погашения кредитов, представленный на рисунке 5.5.1.

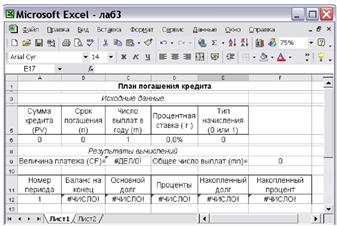
Рисунок 5.2. – Шаблон для разработки планов погашения кредитов

Первая часть этого шаблона предназначена для ввода условий, на основании которых получен (выдан) кредит, т.е. для задания величин PV, r, n. Кроме того, как и в предыдущих случаях, необходимо предусмотреть вариант выплат процентов т раз в году, а также различные типы начисления процентов — в начале или в конце каждого периода. По умолчанию определим: m = 1, тип начисления — 0 (конец периода). Для записи исходных данных удобно использовать табличную форму с более компактным и наглядным их представлением. С учетом оформления, заголовков и таблицы для ввода исходных данных эта часть шаблона будет занимать первые шесть строк электронной таблицы. Перед тем как приступить к проектированию второй части шаблона, целесообразно выполнить еще одну полезную операцию — определить собственные имена для ячеек, в которые будут вводиться исходные данные. Предлагаемые имена для ячеек приведены в таблице 5.1.

Таблица 5.1.

Имена ячеек шаблона

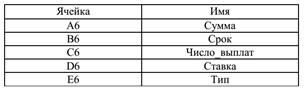
В Excel ячейкам можно присваивать символические имена, определяемые пользователем. Эти имена могут использоваться в качестве адресных ссылок на ячейки, блоки, отдельные значения или формулы. Определение имен — своего рода правило хорошего тона и дает целый ряд преимуществ. Например, формула

=Количество*Цена

несет в себе гораздо больше информации, чем формула

=А1*В1.

В свою очередь формулу в ячейке можно также задать именем, например,

=Выручка,

предварительно определив ее как

=Количество*Цена или =А1*В1.

В общем случае символические имена (именные ссылки) могут быть использованы везде, где можно применить обычные адресные ссылки Excel. При определении имен следует руководствоваться правилами:

• имя должно начинаться с буквы или символа _;

• использование пробелов в именах недопустимо, в качестве разделителей слов следует применять знак _ (например, Число выплат);

• длина имени не должна превышать 255 символов.

Существует несколько способов определения имен. Наиболее простой — использование окна имен, которое расположено в левой части строки ввода Excel. По умолчанию, если имена в рабочей книге не определены, окно имени всегда показывает адрес активной ячейки (например, в новой таблице его содержимым будет ссылка на первую ячейку — А1). Для того чтобы определить имя для ячейки, необходимо выполнить следующие действия:

1) сделать ячейку активной (т.е. установить в нее указатель);

2) щелкнуть мышью по окну имен. При этом ссылка на ячейку будет выделена, а указатель примет вид вертикальной черты.

3) ввести с клавиатуры требуемое имя и нажать клавишу [ENTER].

После выполнения указанных действий при активизации данной ячейки в окне всегда будет показано определенное для нее имя. Задание имен можно также осуществить в режиме диалога, воспользовавшись пунктом Имя темы Вставка главного меню Excel.

Руководствуясь любым способом, определите имена, приведенные в таблице 5.5.1, для соответствующих ячеек шаблона. Продолжим формирование шаблона. Вторая часть шаблона должна содержать результаты вычислений по периодам. Ее можно представить в виде таблицы, состоящей из шести граф: номер периода, баланс на конец периода, сумма основного долга, сумма процентов, сумма накопленного долга, сумма накопленных процентов. Формулы, используемые в шаблоне, приведены в таблице 5.2.

Таблица 5.2.

Формулы шаблона

Обратите внимание на то, что все функции заданы с отрицательным знаком. Это обеспечивает возможность ввода исходных данных и получения результатов вычислений в виде положительных величин, избавляя нас от проблем интерпретации знаков. Кроме того, требование ввода исходных данных в виде положительных величин обусловлено спецификой форматов функций ОБЩПЛАТ и ОБЩДОХОД. Полученная в результате таблица-шаблон должна иметь вид, показанный на рисунке 5.5.1. Наличие ошибок в блоке формул В12:F12 связано с отсутствием исходных данных. Сформированный шаблон требует дополнительных пояснений. Выполняя операции по формированию шаблона, вы уже обратили внимание на способ указания имен ячеек при задании формул. Почему же здесь выбран такой способ адресации? При разработке универсального шаблона для автоматизации расчетов по составлению планов погашения долгосрочных кредитов мы заранее не можем знать, какие сроки проведения операции будут предусмотрены тем или иным контрактом. Известно лишь, что сроки проведения подобных операций составляют не менее одного года (периода). Поэтому при разработке шаблона необходимо предусмотреть возможность выполнения необходимых расчетов по крайней мере для минимально возможного срока проведения операции n = 1. Именно такая «базовая» таблица-шаблон и была сформирована в результате выполнения описанных выше действий. Имея базовый шаблон, можно легко получить таблицу для любого числа периодов, скопировав необходимое количество раз формулы блока В12:F12. Однако в случае использования обычной (относительной) адресации ячеек при выполнении команды копирования произойдет автоматическая перенастройка адресов ячеек в формулах относительно начала блока-получателя, что приведет к искажению общего смысла и ошибкам в вычислениях. Напомним, что параметры PV, r, n, m, тип, принимающие участие в расчетах, являются постоянными на протяжении всего срока проведения операции, тогда как номер периода t должен изменяться от 1 до m*n. Поэтому после выполнения команды копирования при относительном способе адресации только номер периода (изменяемый параметр) в функциях будет указан правильно. Чтобы избежать подобных коллизий в формулах, содержащих постоянные параметры (PV, r, п, т, тип), необходимо использовать метод абсолютной адресации ячеек. Этот вид адресации и обеспечивают в данном случае пользовательские имена, присвоенные ячейкам А6, В6, С6, D6, Е6 (таблица 5.5.1). Кроме того, применение пользовательских имен повышает наглядность формул, делая их более понятными. Ячейка С9 содержит формулу расчета периодического платежа, a F9 — общего числа периодов проведения операции. Значение последней показывает нам также предел копирования формул блока В12:F12. Проверим работоспособность шаблона на примере из предыдущей лабораторной работы.

Пример 1.

Банком выдан кредит в 10 000 ден. ед. на 5 лет под 12% годовых, который должен быть погашен равными долями, выплачиваемыми раз в конце каждого года. Разработать план погашения кредита.

Решение с помощью Excel.

Рассмотрим решение данного примера по этапам.

1. Введите исходные данные в блок ячеек А6:Е6. После ввода данных в ячейке С9 появится результат расчета периодического платежа, а в F9 — общего числа периодов проведения операции.

2. Сделайте активной ячейку А12. Выберите в главном меню тему Правка пункт Заполнить подпункт Прогрессия. На экране появится диалоговое окно подпункта Прогрессия. Сделайте активным переключатель по столбцам и щелкните левой клавишей мыши в поле Предельное значение. Введите число периодов (ячейка F9) в поле Предельное значение. Нажмите кнопку [ОК] или клавишу [ENTER]. Результатом выполнения этих действий будет заполнение ячеек колонки А последовательным рядом чисел, начиная с ячейки А12.

3. Скопируйте формулы из блока В12:F12 необходимое число раз.

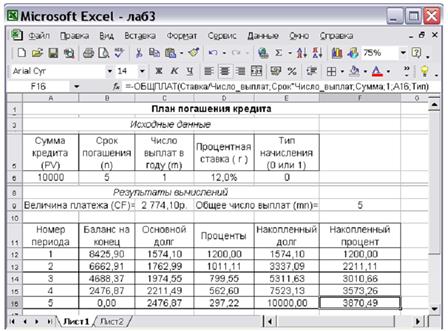
Рисунок 5.3. – План погашения кредита

Полученная в результате таблица будет иметь вид, показанный на рисунке 5.5.2. Указанные в п. 2 операции можно было выполнить и без использования главного меню, произведя следующие действия:

1) сделать активной ячейку А12 и установить указатель мыши на ее нижний правый угол. При этом указатель примет вид маркера заполнения — «+»;

2) нажать клавишу [CTRL] и, не отпуская ее, протащить мышью маркер заполнения необходимое количество раз вниз (по колонке А). При этом в левом углу строки ввода будет выводиться значение счетчика ряда. Разработка подобных процедур позволяет существенно упростить и повысить эффективность решения многих финансовых задач.

Задания для самостоятельного решения

1. Разработайте план погашения кредита, полученного на следующих условиях:

а) 50 000 сроком на 7 лет под 8% годовых при выплате один раз в конце каждого года;

б) 100 000 сроком на 10 лет под 5% годовых при выплате один раз в конце каждого квартала;

с) 75 000 сроком на 3 года под 12% годовых при выплате один раз в конце каждого месяца.

2. Разработайте план погашения кредита, полученного на следующих условиях:

а) 50 000 сроком на 7 лет под 8% годовых при выплате один раз в начале каждого года;

б) 100000 сроком на 10 лет под 5% годовых при выплате один раз в начале каждого квартала;

с) 75 000 сроком на 3 года под 12% годовых при выплате один раз в начале каждого месяца.

3. Коммерческая организация получила банковский кредит в размере 150 тыс. руб. на пятилетний срок с уплатой 10%, начисляемых ежегодно. Погашение кредита и процентных платежей осуществляется равными взносами в течение пяти лет, начиная с конца первого года. Требуется определить размер ежегодных процентных платежей и основной суммы долга по банковскому кредиту.

4. Фирма получила банковский кредит в размере 200 тыс. руб. на трехлетний срок с уплатой 12%, начисляемых ежегодно. Погашение кредита и процентных платежей осуществляется равными взносами в течение пяти лет, начиная с начала первого года. Требуется определить размер ежегодных процентных платежей и основной суммы долга по банковскому кредиту.

5. Коммерческая организация приобретает новое компьютерное оборудование за 25,3 тыс. руб., при этом планируется в течение ближайших 5 лет ежегодно получать экономию затрат по ведению бухгалтерского учета в размере 10 тыс. руб. Средние ставки по банковским депозитам составляют 15% годовых. Оценить целесообразность данной инвестиции в сравнении с альтернативными вложениями средств в банковский депозит.

Контрольные вопросы

1. Какие возможные стратегии погашения кредита в условиях денежного дефицита вам известны?

2. По каким признакам необходимо отсортировать кредиторскую задолженность предприятия при управлении риском непогашения кредита?

3. Что необходимо осуществить для повышения эффективности плана погашения кредита?

4. Как добиться наибольшей оптимизации при разработке плана погашения кредита?

Лабораторная работа 6 (2 часа).

ФИНАНСИРОВАНИЕ РИСКОВ

Управление рисками методами учета фактора времени в финансовых операциях

Цель работы 6 – изучение методов учета фактора времени в финансовых операциях.

Теоретическое основание

В финансовом менеджменте фактор времени учитывается с помощью методов наращения и дисконтирования, в основу которых положена техника процентных вычислений. С помощью этих методов осуществляется приведение денежных сумм, относящихся к различным временным периодам, к требуемому моменту времени в настоящем или будущем. При этом в качестве нормы приведения используется процентная ставка - r. В узком смысле процентная ставка представляет собой цену, уплачиваемую за использование заемных денежных средств. Однако в финансовом менеджменте ее также часто используют в качестве измерителя уровня (нормы) доходности производимых операций, исчисляемого как отношение полученной прибыли к величине вложенных средств и выражаемого в долях единицы (десятичной дробью) либо в процентах. Под наращением понимают процесс увеличения первоначальной суммы в результате начисления процентов. Экономический смысл метода наращения состоит в определении величины, которая будет или может быть получена из некоторой первоначальной (текущей) суммы в результате проведения операции. Другими словами, метод наращения позволяет определить будущую величину (future value - FV) текущей суммы (present value - PV) через некоторый промежуток времени, исходя из заданной процентной ставки r(rate). Дисконтирование представляет собой процесс нахождения величины на заданный момент времени по ее известному или предполагаемому значению в будущем, исходя из заданной процентной ставки. В экономическом смысле величина PV, найденная в процессе дисконтирования, показывает современное (с позиции текущего момента времени) значение будущей величины FV. Нетрудно заметить, что дисконтирование - это по сути зеркальное отражение наращения. Используемую при этом процентную ставку r называют нормой дисконта. В зависимости от условий проведения финансовых операций, как наращение, так и дисконтирование могут осуществляться с применением простых, сложных либо непрерывных процентов. Простые проценты, как правило, используются в краткосрочных финансовых операциях, срок проведения которых меньше года. Базой для исчисления процентов за каждый период в этом случае служит первоначальная (исходная) сумма сделки. В общем случае наращение и дисконтирование по ставке простых процентов осуществляют по формулам:

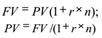
где n — число периодов; r — ставка процентов. Сложные проценты широко применяются в долгосрочных финансовых операциях со сроком проведения более одного года. Они могут использоваться и в краткосрочных финансовых операциях, если это предусмотрено условиями сделки либо вызвано объективной необходимостью (например, высоким уровнем инфляции, риска и т.д.). При этом база для исчисления процентов за период включает в себя как исходную сумму сделки, так и сумму уже накопленных к этому времени процентов. Методы наращения и дисконтирования играют важную роль в финансовом анализе, так как являются инструментарием для оценки потоков платежей CF (cash flows).

Оценка потоков платежей

Проведение практически любой финансовой операции порождает движение денежных средств: возникновение отдельных платежей или множества выплат и поступлений, распределенных во времени. В процессе количественного анализа финансовых операций удобно абстрагироваться от их конкретного экономического содержания и рассматривать порождаемые ими движения денежных средств как численный ряд, состоящий из последовательности распределенных во времени платежей CF0, CF1 ..., CFn. Для обозначения подобного ряда в мировой практике широко используется термин поток платежей, или денежный поток (cash flow), которым необходимо управлять для обеспечения эффективности функционирования организации [15]. Отдельный элемент такого численного ряда CFt представляет собой разность между всеми поступлениями (притоками) денежных средств и их расходованием (оттоками) на конкретном временном отрезке проведения финансовой операции. Таким образом, величина CFt может иметь как положительный, так и отрицательный знак. Количественный анализ денежных потоков, генерируемых за определенный период времени в результате реализации финансовой операции или функционирования каких-либо активов, в общем случае сводится к исчислению следующих характеристик:

FVn - будущей стоимости потока за n периодов;

PVn - современной стоимости потока за n периодов.

Часто возникает необходимость определения и ряда других параметров финансовых операций, важнейшие из которых:

CFt — величина потока платежей в периоде t;

r —процентная ставка;

n — срок (количество периодов) проведения операции.