Схема и некоторые особенности применения метода Монте-Карло

Рассмотрим схему и некоторые особенности применения метода Монте-Карло или, иначе, метода статистических испытаний, на простейшем примере вычисления площадей плоской фигуры.

Пусть произвольная плоская фигура площадью S располагается внутри единичного квадрата площадью 1 (рис. 9.1). Требуется определить площадь этой плоской фигуры S. Имеется несколько способов решения этой задачи от планиметрирования до взвешивания. В данном случае используется другой способ.

В единичном квадрате выбирается N случайных точек. Обозначим через N' число точек, попавших внутрь рассматриваемой фигуры.

Геометрически очевидно, что

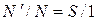, (9.1)

где 1 – площадь единичного квадрата. Отсюда площадь плоской фигуры:

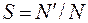(9.2)

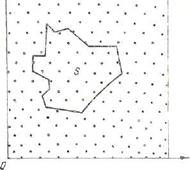
Рис. 9.1. Произвольная плоская фигура в площади единого квадрата.

Для реализации данного примера вычисления площади необходимо было выполнить следующий набор действий.:

1. В площади единичного квадрата (рис. 9.1) случайно выбирается какая то точка. При этом, так как точка выбирается случайно, координаты случайной точки, допустим у₁ и х₁, являются значениями случайных величин Y и X, изменяющихся в пределах от 0 до 1. Затем случайно выбирается вторая точка, затем третья и.т. д. Таким образом, можно сказать, что первое действие для решения задачи о площади плоской фигуры заключается в задании двух значений случайной величины определяющих положение точки в единичном квадрате.

2. Проверяется, принадлежит ли эта точка площади S заданной фигуре (принадлежит ли значение или значения случайных величин интервалу значений данной фигуры);

Первое и второе действие составляют одно случайное испытание. Перед тем как перейти к третьему действию — определению исследуемого признака — случайное испытание повторяется N раз.

3. Находится отношение числа точек, принадлежащих данной фигуре, к общему числу точек в единичном квадрате..

* В общем случае эти пределы могут быть иными.

Изложенный алгоритм во многом отражает суть метода Монте – Карло.

Таким образом, метод Монте-Карло состоит из серии случайных испытаний, подвергнутых последующей статистической обработке. Отсюда другое название метода — метод статистических испытаний.

На приведенном простом примере можно выявить характерные особенности и условия применения метода Монте-Карло.

Первой его особенностью является простая структура вычислительного алгоритма.

Второй особенностью является медленная сходимость метода. Так, погрешность вычислений площадей (экспериментов вообще) методом Монте-Карло медленно уменьшается с увеличением числа испытаний. Можно показать, что эта погрешность пропорцио­нальна корню квадратному из N [ ], т. е.

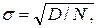(9.3)

где D — некоторая постоянная, N — число испытаний.

Отсюда следует, что для того, чтобы уменьшить погрешность в 10 раз, нужно увеличить число испытаний в 100 раз.

Именно поэтому для применения метода статистических испы­таний обычно используют ЭВМ.

Третьей особенностью метода Монте-Карло является его ис­ключительная универсальность. Как следует из приведенного при­мера, он может быть использован для вычисления площадей и, по аналогичной схеме, объемов, т. е. в общем случае метод может быть использован для вычисления двойных, тройных интегралов и т. д.

Рассмотрим теперь необходимые условия применения метода. Вернемся еще раз к примеру на вычисление площадей. Пусть фигура в площади единичного квадрата на рис. 9.1 представляет собой мишень. Стрелок, находящийся на некотором расстоянии от мишени, стреляет N раз, целясь в центр мишени. Конечно, не все пули будут ложиться в центр мишени. Они пробьют на мишени 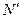случайных точек, распределенных относительно центра по нормальному закону. Можно ли по этим точкам оценить площадь S? Конечно, нет, так как в этом случае получим значительное завышение площади, причем завышение будет тем больше, чем выше квалификация стрелка.

Отсюда следует важный вывод, что площади определяются правильно только в том случае, когда случайные точки (значения случайных величин) равномерно разбросаны по всей площади единичного квадрата, в котором находится рассматриваемая фигура.

Таким образом, для применения стандартной, принятой в гидрологии схемы метода моделирования Монте-Карло необходимо выполнение двух обязательных условий:

1) наличие случайных чисел, равномерно распределенных в заданном интервале. Обычно принимается интервал от 0 до 1. Если границы интервала возможных значений отличаются от заданного, то они легко приводятся к нему;

2) разработка приема определения области (площади, отрезка кривой, точки), куда попадают случайные числа.

Числа, удовлетворяющие первому условию, называются случайными числами, равномерно распределенными в интервале, от 0 до 1. Обычно они обозначаются α (могут быть и другие обозначения).

Пример определения площади плоской фигуры был использован для уяснения общей схемы и некоторых особенностей метода Монте-Карло. Покажем теперь, что этот же метод — метод статистических испытаний — может быть использован для моделирования различных гидрологических процессов. С этой целью, в качестве введения к более сложным схемам, рассмотрим моделирование наиболее простых процессов, значения которых могут быть представлены в виде последовательности значений дискретной случайной величины. Предваряя последующее изложение, заметим также, что в тех случаях, когда моделирование производится не по какому-либо конкретному ряду, а по заданным характеристикам распределения процесс моделирования часто называется розыгрышем.