Связь между параметрами и видом движения жидкостей

Скорость и ускорение

Положение частицы жидкой среды в произвольный момент времени t описывается координатами x=x(t), y=y(t), z=z(t) в прямоугольной системе координат или радиус-вектором 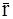=(x, y, z)^T ( ).

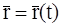Основой описания движения жидкой среды методом Эйлера является векторное поле скоростей 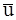=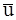(x,y,z,t), где 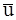=(u_x, u_y, u_z)^T – скорость частицы, находящейся в момент времени t в точке с координатами x, y, z.

Скорость связана с изменением положения частицы d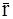обычным соотношением 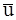=d/d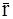t=(dx/dt, dy/dt, dz/dt)^Т и, соответственно u_x=dx/dt, u_y=dy/dt, u_z= dz/dt.

Внимание! Это соотношение справедливо лишь в указанном случае, когда d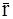описывает перемещение частицы из рассматриваемой точки, т.е. – является дифференциалом ее траектории. Из рассматриваемой точки (x, y, z), можно дать разные приращения d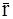=(dx, dy, dz)^T,но лишь одно из них равно 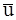dt=(u_xdt, u_ydt, u_zdt)^T, а именно – то, которое удовлетворяет уравнению касательной 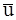´ 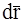=0, или dx/u_x=dy/u_y=dz/u_z.

Огибающая скоростей в каждой точке (для рассматриваемого момента времени), или линия, касательная к которой в каждой точке совпадает с мгновенным направлением скорости в этой точке, называется линией тока. Таким образом уравнение 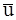´ 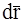=0, или эквивалентные ему соотношения dx/u_x=dy/u_y=dz/u_z являются уравнениями линии тока.

Ускорение частицы 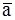=(a_x, a_y, a_z)^T в произвольной точке в момент времени t также является полем 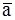=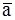(x,y,z,t). Ускорение в каждой точке представляет собой полную производную скорости в этой точке, т.е. 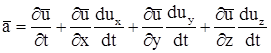, где dx, dy, dz – не произвольные приращения, а те, которые определяются движения частицы из рассматриваемой точки. Следовательно,

.

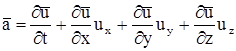Первое слагаемое называется локальным ускорением. Оно характеризует изменение местной скорости в той же точке со временем. Остальные называются конвективными (конвекционными) и показывают изменение скорости в пространстве. Проекции ускорения по осям имеют вид

;

;

.

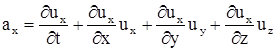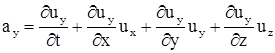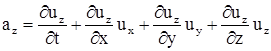Входящие в эти выражения производные проекций скорости по изменениям координат принято делить на прямые (продольные) 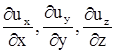и косые (поперечные) 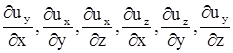. Такие же названия используют для соответствующих составляющих проекций конвективного ускорения по координатным осям: 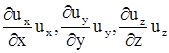- прямые (продольные) и 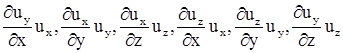- косые (поперечные) составляющие конвективного ускорения.

В общем случае ускорение можно записать в виде .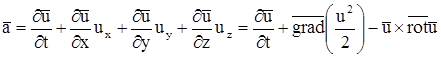

Чтобы убедится в этом, достаточно рассмотреть одну из проекций ускорения и выполнить очевидные преобразования:

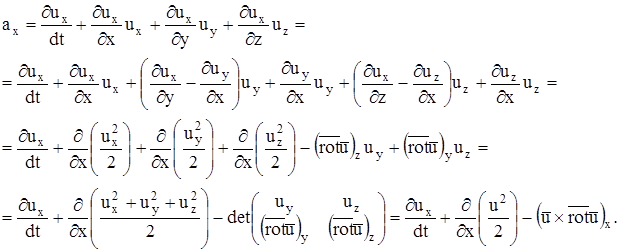
Здесь 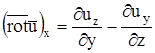, , 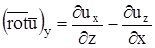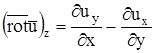- проекции ротора.

Проделав это с остальными проекциями, можно получить указанное выше выражение ускорения.

Связь между параметрами и видом движения жидкостей

Наличие или отсутствие тех или иных составляющих скорости, а также их производных, или особые соотношения между ними определяют вид или особые случаи движения.

Движение называется стационарным (установившимся), если 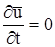, т.е. отсутствует локальное ускорение. Если локальное ускорение не равно нулю, то движение называют нестационарным, или неустановившимся.

Далее для упрощения движение будет предполагаться установившимся.

При выявления особых видов или составляющих движения удобно рассмотреть для произвольной системы координат элементарный объем в виде прямоугольного тетраэдра, вершина О которого находится в начале координат, а три ребра - вдоль осей этой системы (рис. 1а). Длины этих ребер - dx, dy, dz соответственно.

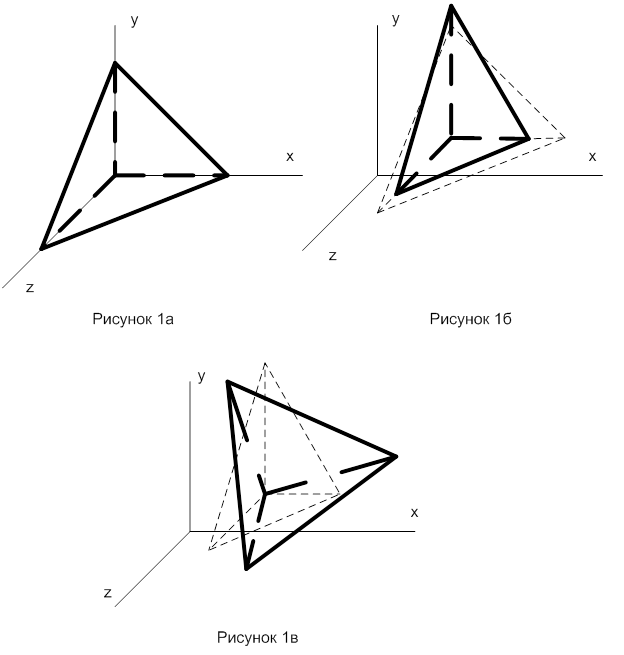
Если отсутствуют конвективные ускорения, т.е. скорости во всех точках выделенного объема 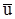одинаковы, то выделенный объем будет двигаться как твердое тело, причем - поступательно, и через интервал времени dt займет положение, показанное на рис. 1в пунктиром. Каждая точка переместиться на .

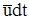Если нулю равны только косые составляющие ускорения, а прямые - имеют ненулевые значения, то за dt точки выделенного объема переместятся на различные расстояния, в частности, вершины тетраэдра переместятся на 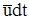, , 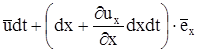, 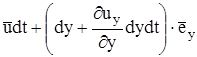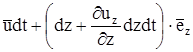соответственно, где 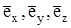- орты осей системы координат. Это положение выделенного объема показано на рис.1б сплошными линиями и на рис.1в - пунктиром. Очевидно, что при этом перемещении выделенный объем деформировался. Например, расстояние вдоль осей между вершинами тетраэдра изменится от dx, dy, dz до 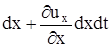, , 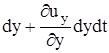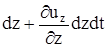соответственно. Величина деформации вдоль осей (линейной деформации) равна 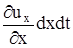, , 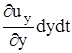, 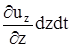относительной деформации - 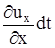, , 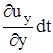, 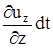а относительной деформации в единицу времени (скорости деформации) - , , .

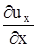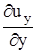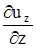Очевидно, что для твердого тела такое движение невозможно. Там проекции скорости на линию, соединяющую каждую пару точек, должны совпадать.

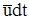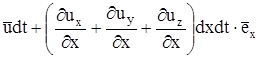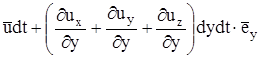
Если косые производные также не равны нулю, то положение вершин тетраэдра будет определяться соотношениями , , , 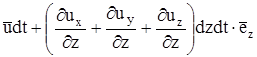т.е. ребра тетраэдра не только изменят длину, но и повернутся на величину, определяемую косыми производными.

Для твердого тела косые производные должны быть связаны соотношениями 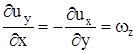, , 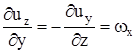, 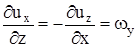так как все точки недеформируемого тела должны иметь одинаковую угловую скорость .

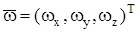Таким образом, наличие ненулевых прямых (продольных) составляющих ускорения, а также нарушение соотношений для косых (поперечных) составляющих приводит к деформации рассматриваемого элементарного объема, величина которой может быть определена по этим составляющим. Для простоты рассматривается случай плоского движения, т.е. когда u_z=0, 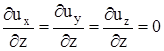(заметим, что в этом случае элементарный объем удобнее взять в виде призмы единичной высоты с основанием ОАВ (в этом случае очевиден переход от плоскости к объему), а не тетраэдра). Обобщение на пространственный случай, как увидим из вывода - также очевидно.

При нулевых косых производных грань (треугольник) ОАВ (см. рис. 2, где ОА=dx, ОВ=dy) преобразуется в треугольник О'А'В'.

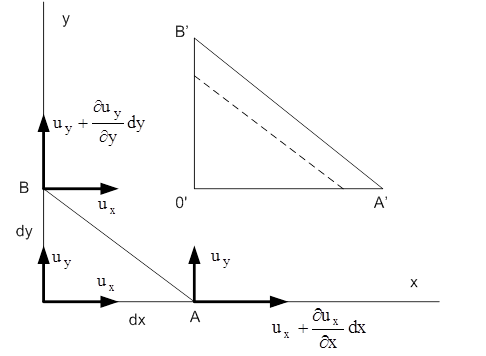
Рисунок 2

Величина объемной деформации dw, т.е. изменения объема, с учетом единичной длины вдоль оси z, равна

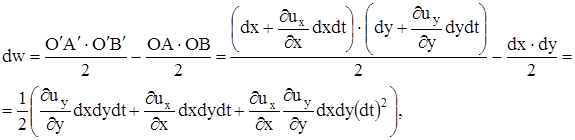
или, оставляя слагаемые одного порядка малости 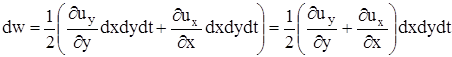. Относительная объемная деформация равна 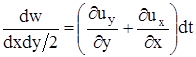, а относительная объемная деформация в единицу времени, или скорость объемной деформации равна .

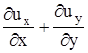Если движение не плоское, то, проделав аналогичные выкладки для элементарного объема в виде тетраэдра или прямоугольного параллелепипеда, можно получить, что относительная объемная деформация в единицу времени (скорость объемной деформации) в общем случае равна

.

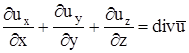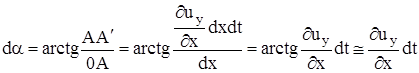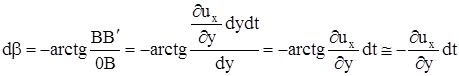При ненулевых поперечных ускорениях ребра рассматриваемого объема перестанут быть параллельными координатным осям. Например, при плоском движении ребра ОА и ОВ (см. рис. 3) повернутся на углы и соответственно, т.е. грань (треугольник) ОАВ трансформируется в треугольник ОА''В''. Для наглядности (но - без потери общности, так как это не меняет выражений для углов da и db) здесь не показаны рассмотренные выше поступательное движение и объемная деформация. Знак минус в выражении для db объясняется тем, что положительному приращению в направлении оси х соответствует отрицательное приращение угла b.

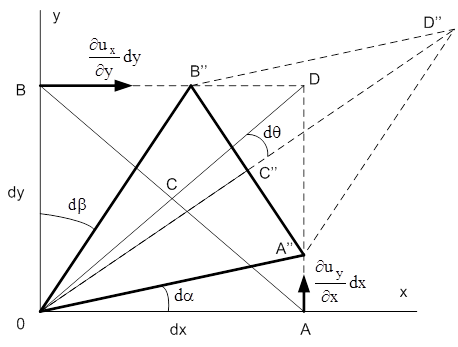
Рисунок 3

Смещения точки А" по х и В" по у являются величинами большего порядка малости, из-за чего на рисунке не показаны.

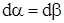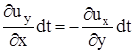Очевидно, что такая трансформация соответствует и повороту и деформации рассматриваемого объема (треугольника). Если этот треугольник представить множеством отрезков, начинающихся в вершине О и заканчивающихся на противолежащей к этой вершине стороне, то при отсутствии деформации все эти отрезки повернулись бы на одинаковый угол (как в твердом теле), т.е. условие отсутствия деформации , или , или 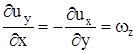. При одновременной с поворотом деформации углы поворота этих отрезков становятся разными 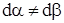. В этом случае в качестве угла поворота естественно принять средний угол поворота этих отрезков, т.е. 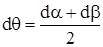. Очевидно, что это тот угол, на который повернется биссектриса ОС треугольника ОАВ при его трансформации в треугольник ОА''В'' (биссектриса примет при этом положение ОС'').

Отсутствию вращения при наличии деформации соответствует нулевое значение этого угла 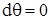, или 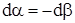(т.е. - сохранение положения биссектрисы). Поэтому совпадающую с биссектрисой ось называют осью деформации, а в качестве угла деформации принимают разницу между углам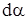и и 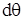, или, что то же самое с учетом знака - между углам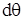и и 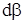, т.е. 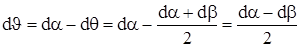. Угловые деформации называют также деформациями сдвига, так как при такой деформации параллельные отрезки смещаются относительно друг друга (например, отрезки OA” и BD” на рис.3). Угол сдвига 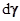показывает на сколько изменился при деформации первоначально прямой угол (например, между отрезками OA и OB). Очевидно, что .

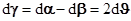Итак, косые составляющие ускорения при плоском движении приводят к повороту оси деформации на угол 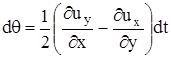и угловой деформации относительно этой оси на угол .

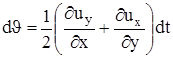Угловая скорость вращения вокруг оси z 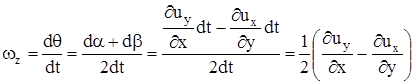, а скорость изменения угла деформации, называемая также скоростью угловой деформации .

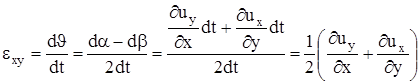Скорость деформации сдвига .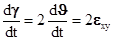

Если движение не плоское, то, проделав аналогичные выкладки для элементарного объема в виде тетраэдра или прямоугольного параллелепипеда, можно получить, что в общем случае угловые скорости вокруг осей определяются выражениями

, , ,

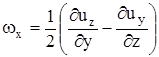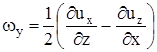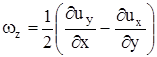а скорости угловой деформации - выражениями

, , .

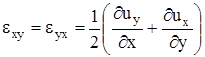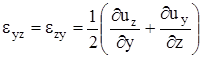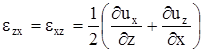Выражения для угловых скоростей в точности совпадают с проекциями ротора скорости 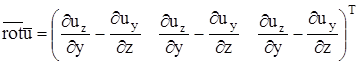, деленными пополам, т.е. 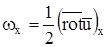, , 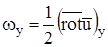, 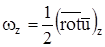или .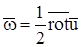

Заметим, что полученные выражения угловых скоростей справедливы и для твердых тел, так как для них 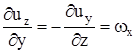, , 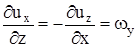, 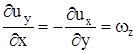при этом скорости угловой деформации тождественно равны нулю.

Следует заметить, что при ненулевых косых производных происходит не только поворот и угловые деформации (сдвига), но одновременно - и линейные деформации растяжения вдоль оси OD и сжатия вдоль оси AB.

При этом деформация из-за косых составляющих ускорения при нулевых прямых составляющих не меняет величины элементарного объема. В этом можно убедится, сравнив площади треугольников ОАВ и ОА''В'', которые при плоском движении соответствуют объему призм единичной длины вдоль оси z. Площадь треугольника ОА''В'' (см. рис.3), очевидно, равна площади прямоугольника OADB (показанного пунктиром) за вычетом площадей треугольников ОАА'', ОВВ'' и А''В''D

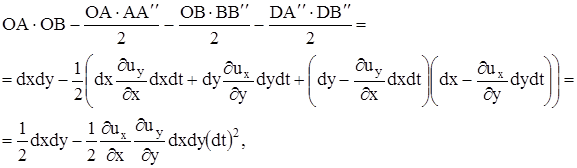
т.е. с точностью до бесконечно малых величин высшего порядка совпадает с площадью треугольника ОАВ, очевидно, равной .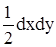

Если движение не плоское, то в неизменности элементарного объема при наличии только косых составляющих ускорения можно убедиться, проделав аналогичные выкладки для элементарного объема в виде тетраэдра или прямоугольного параллелепипеда. Несложно убедиться и в том, что при этом отсутствует и линейная деформация, т.е. длина любого малого отрезка dl изменится на величину более высокого порядка малости. Например, отрезок ОА на рис.3 длиной dx перейдет в отрезок ОА'', длина которого .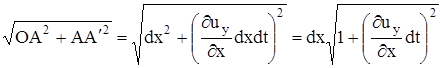

Поэтому деформация при наличии только косых составляющих ускорения называется угловой деформацией или деформацией сдвига, в отличие от объемной деформации, возникающей при ненулевых прямых составляющих ускорения.

Для описания общей деформации, или деформационного движения жидкости вводят матрицу скоростей деформации 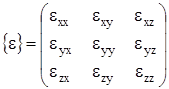, называемую также тензором деформации, элементы которой 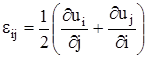, 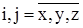. Как видно из полученных выше соотношений, диагональные элементы этой матрицы, определяемые прямыми производными скорости, показывают скорость относительной деформации вдоль осей (деформации растяжения-сжатия, приводящей к изменению объема), а внедиагональные, определяемые косыми производными, являются скоростями угловой деформации.

Таким образом, движение в окрестности любой рассматриваемой точки жидкости можно представить состоящим из движений трех видов: поступательного (определяемого скоростью в этой точке), вращательного относительно этой точки и деформационного. Два последние вида движения определяются конвективными производными скорости.

Формально этот факт принято записывать в виде соотношения, связывающего скорости в двух близких точках установившегося течения. Если, например, известны скорость и ее конвективные производные в произвольной точке А, то скорость в близкой к ней точке В, очевидно, можно найти из соотношения 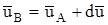, где 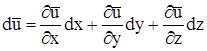. Здесь dx, dy, dz - составляющие вектора 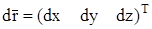), соединяющего точку А с точкой В.

Проекция дифференциала скорости вдоль оси х

.

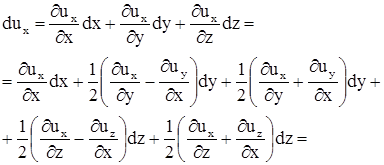
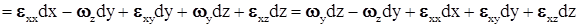Последнее выражение можно представить в виде

,

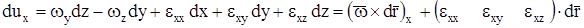или в виде

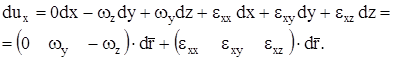
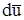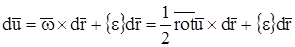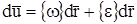Проделав аналогичные действия для остальных проекций вектора , легко получить, что , или , где 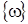- матрица, составленная из проекций вектора угловых скоростей : .

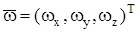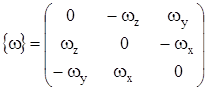Таким образом

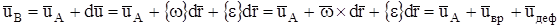, где 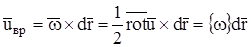- скорость вращения (поворота), а 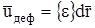- скорость деформации. Это соотношение известно как теорема Гельмгольца о составляющих скорости течения.

Сравнить с соотношением для твердых тел.

Особые случаи движения жидкостей.

1. Движение при отсутствии объемных деформаций, условием которого является .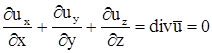

Для сплошных несжимаемых жидкостей, в которых невозможны объемные деформации, это уравнение должно выполняться при любом характере их движения. Для таких жидкостей невыполнение этого уравнения возможно лишь при разрывах (нарушениях сплошности) среды. Поэтому уравнение 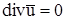является условием неразрывности и называется уравнением неразрывности.

2. Движение при отсутствии вращения частиц, или безвихревое движение, условие которого ,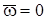

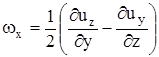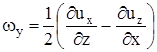или =0, 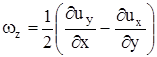=0, =0,

или , , .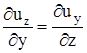

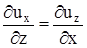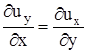Безвихревым такое движение называется потому, что условие 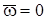эквивалентно 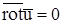(так как 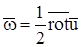), а ротор имеет эквивалентное название вихрь.

Безвихревое движение (течение) называется также потенциальным, так как при таком движении поле скоростей является потенциальным, т.е., для каждой точки этого поля существует функция 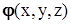, называемая потенциалом, градиент которой совпадает с вектором скорост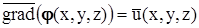и , или , , .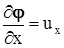

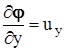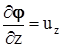Другими словами, если равенства 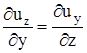, , 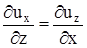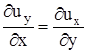выполняются, то существует функция 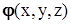, являющаяся решением системы уравнений 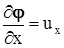, , 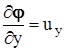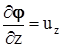. Это утверждение не требует специального доказательства, так как почти точно совпадает с известной из математического анализа теоремой Фробениуса о существовании и единственности решения систем уравнений в частных производных, точнее - со следствием, или частным случаем этой фундаментальной теоремы для системы уравнений вида 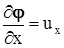, , 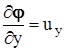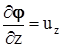. Для полного совпадения нужно, чтобы существовали все вторые производные функций 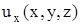, , 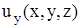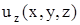). Нужно также обратить внимание, что по теореме Фробениуса такая функция 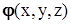существует для малых или односвязных окрестностей рассматриваемой точки.

Легко также увидеть, что всякое потенциальное поле является безвихревым. Доказательством этому служит известный положение о тождественном равенстве нулю ротора градиента любой функции. Действительно, если поле потенциально (т.е., существует функция 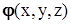, такая, ч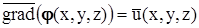то ), то 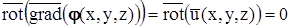, т.е. такое поле является безвихревым.

Это же доказательство в непосредственном виде сводится к определению всех вторых смешанных частных производных функции 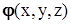по независимым переменным x, y, z и использованию их попарных равенств. Например, 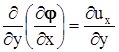, 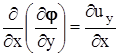при тождестве 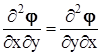приводит к одному из равенств, определяющих безвихревой характер движения 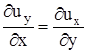. Аналогично можно прийти к остальным равенствам.

При безвихревом (потенциальном) движении 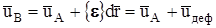, а выражение для ускорения приобретает вид .

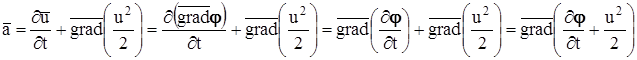В качестве особых случаев движения жидкости иногда выделяют также течение без деформаций, т.е. - совпадающее с движением твердого тела («консервативное течение», или «отвердевшее течение») и поступательное течение, при которых 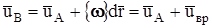и 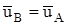соответственно.