Сарос. тұтылуды бақылаудың ғылыми мағнасы.

Негізгі әдебиеттер:

1. Кононович Э.В., Мороз В.И. Общий курс астрономии.-М:УРСС,2001.-544бет

2. Рамазанова С., Тоқсеитова Р. Астрономия. Шымкент. 2009. 238бет.

3. Рамазанова С., Садық Б. Жалпы астрономия курсынан зертханалық практикум. Шымкент.

2008. 54 бет.

4. Рамазанова С. Астрономия пәнінен практикалық сабақтарға арналған оқу-әдістемелік құрал.

Шымкент. 2010.

5. Дагаев М.М., ДеминВ.Г., Климишин И.В., Чаругин В.М. Астрономия.-М.:Просвещение. 1983,

384бет.

6. Курышев В.И. Практикум по астрономии.-М.:Просвещение.1986, 144бет.

7. Дагаев М,М, Лабораторный практикум по курсу общей астрономии.-М.:Просвещение. 1980,

128бет.

8.Дагаев М.М. Наблюдения звездного неба.-М.:Наука,1980, 454бет.

Қосымша әдебиеттер:

1.Климишин И.А. Астрономия наших дней. –М.:Наука,1980,456бет.

2.АндриановИ.К., МарленскийА.Д. Астрономические наблюдения в школе.-М.:

Просвещение.1987, 112бет.

3.КуликовскийП.Г. Справочник любителя астрономии.-М.:Физматгиз.1961, 494бет.

4.Физика космоса. Маленькая энциклопедия.-М.:Советская энциклопедия. 1986, 783бет.

5.Лейзер Д. Создавая картину Вселенной. –М.:Мир. 1988, 324бет.

11-ші лекция.Аспан механикасының негідері, бүкіл элемдік тартылыс заң. Планеталық орбиталардың элементтері. Тартылыс заңның әмбебаптылығы. Кеплердің жалпылама заңдары. Аспан денелерінің массаларын анықтау. Ауытқу теориясының элементтері. Плутон және Нептун планеталарының ашылуы.

Кеплердің заңдары планеталар дүниесінің бір дұрыс жүйе екенін көрсетті. Сондықтан барлық планеталарды Күнмен байланыстыратын, олардың қозғалысын реттейтін «күш» барлығы туралы идея дами бастайды.

Тартылыс күшінің бар екендігін, оның аралыққа байланысты өзгеретінің ХVII ғ. ғалымдар талқылай бастады. Әуелі Италия оқымыстысы Борелли, онан кейін Галилей, Ньютонның замандасы Гук, ақырында Ньютон табиғаттың ең бір негізгі заңы бүкіл әлемдік тартылыс заңын математикамен негіздеп, ол арқылы тек Жердегі құбылысты ғана емес Күн жүйедегі құбылысты да түсіндірді.

1687 жылы баспадан Ньютонның атақты еңбегі «Табиғат философиясының математикалық бастамысы» /Математические начала натуральной философии/ жарыққа шығады. Оның ақырғы кітабында мынадай теорема айтылып дәлелденеді:

«Басты планеталарды түзу сызқты қозғалыстан үнемі бұратын күштер Күнге қарай бағытталған және Күнмен планетаның ара қашықтығының квадраттарына кері пропорционал болады».

Осы теореманы Ньютон Айға қолданып, Айдың өз орбитасында ұстайтын күш Жер бетіндегі ауырлық күшпен тепе-тең екенін дәлелдейді. Еркін құлаған дененің Жер бетіндегі үдеуін 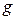– деп, Ай қашықтығындағы үдеуін 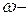деп, Жердің массасын 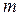, радиусын 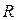, Ай мен Жердің қашықтығы 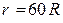, гравитациялық тұрақты 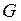. Сонда, 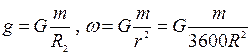. Осы екі өрнекті салыстырып 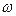-ны есептесек, 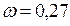см/с².

Енді Айдың орбиталық қозғалысының центрге тартқыш үдеуін есептейік. Бұл үдеуді мына өрнекпен анықтаймыз:

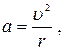
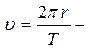Айдың орбиталық жылдамдығы,

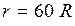– Айдың орбиталық радиусі,

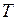– Айдың айналу периоды.

Сонда,

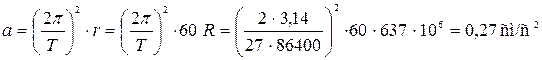
жоғарғы нәтижемен бірдей шықты.

Осыдан Ньютон қорытынды жасайды: Жер бетіндегі ауырлық күш Айды да өз орбитасында ұстап тұрады екен.

Бұл күштің өрнегін Кеплер заңдарынан қорытуға болады. Кеплердің І заңы бойынша планетаның орбитасы эллипс, оның бір фокусында Күн тұрады. Осы фокусты координат жүйесінің басы етіп алып орбитаның теңдеуін полярлық координат жүйесінде өрнектейік:

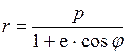(1)

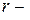планетаның радиус – векторы,

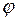– полярлық бұрыш,

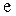– эксцентриситет,

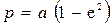– орбитаның параметрлері,

– орбитаның үлкен жарты осі.

Кеплердің ІІ заңы математикалық түрде мынадай өрнекпен жазылады:

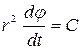(2)

С – екі еселенген секторлық жылдамдық,

Кеплердің ІІІ заңы бойынша

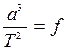(3)

Т – айналу период,

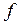– барлық планеталар үшін жалпы тұрақты.

Күштін өрнегін анықтау үшін кинетикалық энергияның теңдеуін дифференциалды түрде жазамыз. Кинетикалық энергияның өсімшесі жұмысқа тең, ендеше:

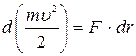(4)

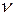– планетаның сызықты жылдамдығы,

– планетаның массасы,

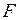– Күнге қарай әсер ететін күш.

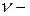ны полярлық координаттарда өрнектеп (4) теңдеуге 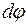-ді ендірсек, мынадай нәтиже аламыз:

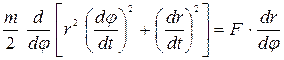(5)

(2) теңдеуден: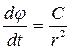

Сонда: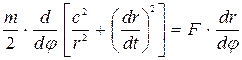

Жақшаны туынды алып ашамыз, сонда:

,

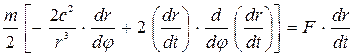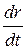– ны алмастырайық: 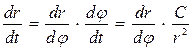немесе

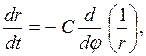ал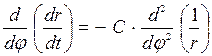

Бұл нәтижелерді жоғарғы теңдікке ендірсек, сонда:

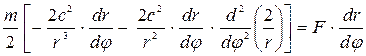
Жақшадан - 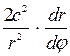шығарамыз және 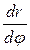- ге қысқартамыз:

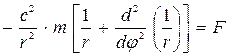(6)

Енді (1) теңдеуден 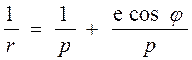, ал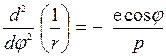

Осыларды (6) теңдеуге еңдірсек:

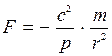, немесе (8) 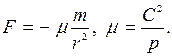8 теңдеуден күштің тартылыс күші екені және оның қашықтықтың квадратына кері пропорционалдығын көреміз. Енді 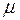коэффициентінің барлық планеталар үшін тұрақты екенін көрсетейік.

Планетаның секторлық жылдамдығы 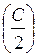радиус-вектордың бірлік уақыт аралығындағы сызатын ауданы. Планетаның айналу периоды Т болатын болса, эллипстің ауданын С, және Т арқылы өрнектейік:

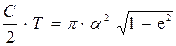, осыдан 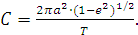Бұны теңдеуге ендірсек:

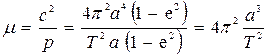
Кеплердің ІІІ заңы бойынша 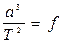, сондықтан 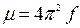– тұрақты. Демек 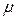барлық планеталар үшін ортақ тұрақты екен.

Планета Күнге массасына пропорционал, ал қашықтықтың квадратына кері пропорционал күшпен тартылады. Ньютонның ІІІ заңы бойынша Күнде планетаға осындай күшпен тартылады.

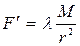(10), немесе 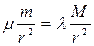. Осыдан, 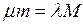, яғни 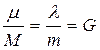тұрақты. Сонда 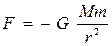(11)

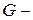гравитациялық тұрақты және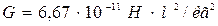

Кез келген массалары 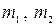ге тең материалдық нүктелер үшін (11) өрнекті былай жазамыз:

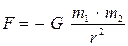, яғни

Кез келген екі материалдық нүкте массаларына тура пропорционал ал қашықтықтарының квадратына кері пропорционал күшпен тартылады.

Бүкіл әлемдік тартылыс заңы тек материалдық нүктелерге дүрыс келеді. Тартылыс күш тартылатын денелердің формаларына тәуелді болады. Ньютон осы заңның массаларының таралуы сфералық-симметриялық болатын денелерге қатысты дұрыс орындалатындығын дәлелдеген. Аспан денелерінің /Жер, Күн, Ай, планеталар, жұлдыздар/ формалары шар тәрізді және массаларының таралуы сфералық болғандықтан оларға бүкіл әлем тартылыс заңын осы формасында қолдануға болады /бірінші жуықтау бойынша/.

Бүкіл әлемдік тартылыс заңы және динамиканың ІІ заңынан мынадай салдар шығады:

1. Екі материалдық нүкте бір біріне шамалары тең күштермен тартылады. Ал үдеулерінің шамалары массаларына кері пропорционал болады.

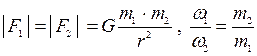
2. Екі материалдық нүктелердің салыстырмалы үдеуі олардың массаларының қосындысына пропорционал болады.

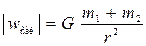
3. Егерде массалары 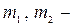ге тең екі материалдық нүктелер үшінші массасы 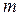материалдық нүктеден бірдей 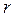қашықтықта орналасатын болса, олар үшінші нүктеге қарай шамалары бірдей болмайтын

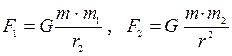күштермен тартылады да, ал үшінші денеден алатын үдеулері тең 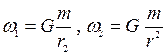болады. Мысалы: Жер, Ай, Күн.