Расчетное определение пределов прочности льда

МОРСКАЯ ЛЕДОТЕХНИКА

РАСЧЕТНЫЕ РАБОТЫ

Учебное пособие

Санкт – Петербург

УДК

ББК

Т

Сазонов К.Е.

Морская ледотехника. Расчетные работы. Учебное пособие. – СПб: ФГУП «Крыловский государственный научный центр», 2016, с.: ил.

Учебное пособие содержит описание расчетных работ по курсу «Морскаяледотехника». Расчетные работы посвящены определению физико-механических свойств льда, расчету ледового сопротивления ледоколов и судов ледового плавания, а также способам теоретической оценки глобальной и локальной ледовых нагрузок на морские инженерные сооружения. Пособие предназначено для студентов, обучающихся по специальностям «Кораблестроение» и «Океанотехника».

УДК

ББК

ÓК.Е.Сазонов, 2016.

ÓФГУП «Крыловский государственный научный центр», 2016.

Оглавление

Предисловие………………………………………………………………………………..
Расчетная работа № 1.Расчетное определение пределов прочности льда………….
Расчетная работа № 2Определение сопротивления судна в сплошных ровных и битых льдах, определение характеристик его ледовой ходкости…………………………...
Расчетная работа № 3Определение толщины ледяного покрова и параметров смерзаемости ледяного канала. Расчет сопротивления судна при движении в канале
Расчетная работа № 4. Определение ледового сопротивления судна по данным модельного эксперимента………
Расчетная работа № 5. Расчет ледовой нагрузки на цилиндрическую вертикальную опору………………………………………………………….
Расчетная работа № 6. Расчет ледовой нагрузки на коническую опору …………
Расчетная работа № 7. Расчет давления льда на единичную опору при термическом расширении……….

Требования к выполнению работ

Рекомендуемая литература

Предисловие

Учебный курс "Морскаяледотехника" читается студентам старших курсов ФКО с целью дать им необходимые сведения об особенностях взаимодействия различных объетов морской техники со льдом. Курс "Морскаяледотехника" разбит примерно на две равные части. В первой части курса дается описание ледяного покрова с физико-географической точки зрения и с точки зрения физики твердого тела, а также изучается взаимодействие с ледяным покровом ледоколов и судов ледового плавания. Во второй части курса рассматривается воздействие льда на различные морские инженерные сооружения, большинство из которых предназначено для добычи углеводородного сырья на шельфе замерзающих морей.

Расчетные работы также можно разбить на две части. В первой работе изучаются приемы численного определения механических свойств морского льда. В последующих двух работах выполняются расчеты ледового сопротивления судна при его движении в различных ледовых условиях. Работа №4 дает учащимся представление о методах обработки данных модельного эксперимента в ледовом бассейне при определении характеристик ледового сопротивления судна.

В последних трех работах изучаются методы определения расчета глобальной ледовой нагрузки на морские инженерные сооружения.

Структура описания каждой лабораторной работы традиционная. Некоторые расчетные формулы приводятся в работе без вывода. Вывод формул должен быть выполнен студентами самостоятельно. Число исходных данных к каждой работе ограничено 10 вариантами.

Отчеты по лабораторным работам оформляются так же, как и в других учебных курсах, и обязательно содержат физический анализ полученных результатов.

Расчетная работа № 1

Расчетное определение пределов прочности льда

Литература

1. Гладков М.Г., Петров Г.И., Федоров Б.А. Схема расчета предела прочности льда. /Труды ААНИИ, т.379, 1983, с.75-88.
2. Морской лед. Сбор и анализ данных наблюдений, физические свойства и прогнозирование ледовых условий. Под ред. И.Е. Фролова и В.П.Гаврило. СПб, Гидрометеоиздат, 1997, 402 с.

Общие пояснения

При осуществлении хозяйственной деятельности в полярных регионах часто возникает необходимость получения информации о прочностных свойствах льда. Получение этой информации традиционным путем с помощью проведения механических испытаний не всегда возможно, т.к. требует больших временных затрат. Кроме этого для выполнения механических испытаний необходимо иметь специальное оборудование, обеспечивающее их выполнение. Поэтому для получения оперативных оценок прочностных свойств льда используют различные косвенные измерения. Следует подчеркнуть, что такими способами можно получить лишь оценки средних величин значений пределов прочности. Подобные методики не содержат информации о случайной изменчивости пределов прочности льда.

Данные многолетних исследований показывают, предел прочности льда для любого типа деформации (сжатие, изгиб и срез) определяется следующими параметрами:

- соленостью льда 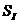, ⁰/₀₀;

- температурой льда 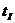, ⁰С;

- структурой льда;

- плотностью льда, кг/м³

- размерами образца.

На результаты определения пределов прочности льда существенное влияние оказывают условия проведения эксперимента. К ним обычно относят:

- свойства среды, в которой находится испытываемый образец льда;

- направление приложения нагрузки относительно ориентации основных структурных элементов льда (кристаллов, блоков кристаллов, рассолосодержащих каналов, воздушных полостей);

- скорость нагружения образцов льда.

Для учета всех этих факторов при определении пределов прочности льда применяют математические выражения, имеющие следующую структуру:

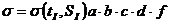, (1.1)

где 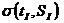- обобщенный предел прочности льда при заданном виде деформации, зависящий от температуры льда и его солености; a, b, c, d и f –поправки, учитывающие влияние структуры льда (а), плотности льда (b), свойств среды (с), направления приложенной к образцу нагрузки (d) и скорости нагружения образца (f). Данные, на основе которых находятся зависимости 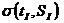, получают путем испытаний малых образцов льда.

В общем виде расчетную схему, базирующуюся на соотношении (1.1) можно представить следующим образом.

1. По семейству графиков, полученных при обобщении экспериментальных данных и отражающих зависимость пределов прочности малого образца льда от типа деформации, температуры и солености, находится обобщенный предел прочности льда .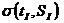

2. В полученное значение вводятся поправки, учитывающие влияние структуры льда, его плотности, свойств среды, направления приложения к образцу нагрузки и скорости нагружения.

Методика выполнения работы

Теоретические основы

Сотрудником ААНИИ Н.В.Черепановым была разработана структурно–генетическая классификация льда по условиям его образования и солености воды. Льды природных водоемов подразделяются на четыре основные группы:

- группа "А" – льды, образующиеся из пресной или сильно распресненной воды соленостью менее 2 ⁰/₀₀;

- группа "Б" – льды, образующиеся в распресненной воде соленостью от 2 до 24.7 ⁰/₀₀;

- группа "В" – льды, образующиеся в морской воде соленостью более 24.7 ⁰/₀₀;

- группа "Г" – льды, претерпевшие термические преобразования в процессе своего существования.

Различные типы льдов, принадлежащих одной группе, имеют различный числовой индекс, который показывает степень динамичности условий ледообразования. Чем выше индекс, тем динамичнее условия. В таблице 1.1 представлена взаимосвязь различных видов ледообразования с формированием определенных структурно генетических типов льда. Основные типы пресноводных и морских льдов представлены на рис. 1.1 и 1.2. Более подробное их описание изложено в справочном пособии [2].

Таблица 5.1

Виды ледообразования и формирование структурно-генетических типов льда

Вид ледообразо-вания	Конжеля-ционное	Конжеляционно-внутриводное	Внутри-водно-шуговое	Инфиль-трационное	Вторично-рекристал-лизационное
Тип льда	А1, А2, А3, А4, Б1, Б2, Б3, Б4, В1, В2, В3	А5. А6, Б5, Б6, В4, В5, В6	А7, А8, Б7, Б8, В7, В8	А9, Б9, В9	Г1, Г2, Г3, Г4

Далее при рассмотрении влияния структуры льда на его прочностные характеристики все расчетные данные будут приводится для двух наиболее распространенных групп льда, а именно для групп "А" и "В". В первом приближении расчетные данные для группы "Б" могут быть получены как среднее значение между соответствующими значениями групп "А" и "В".

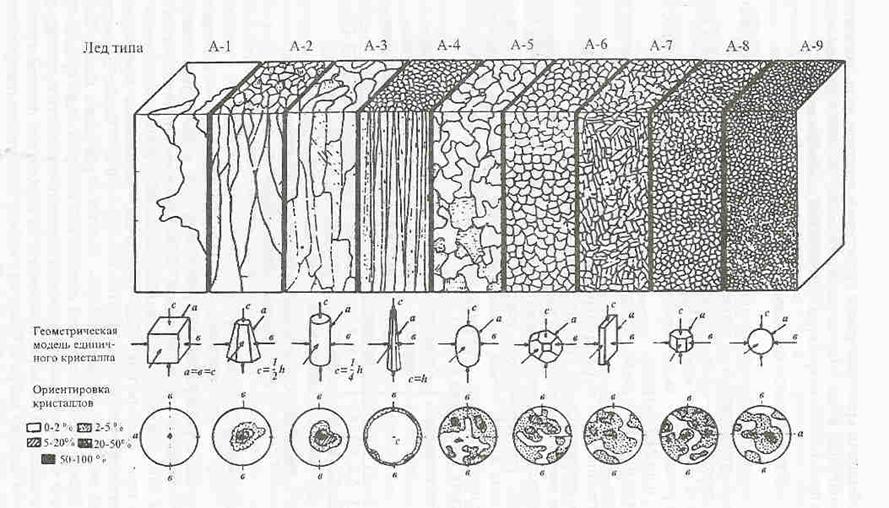
Рис. 1.1. Основные типы пресноводных льдов (группа "А").

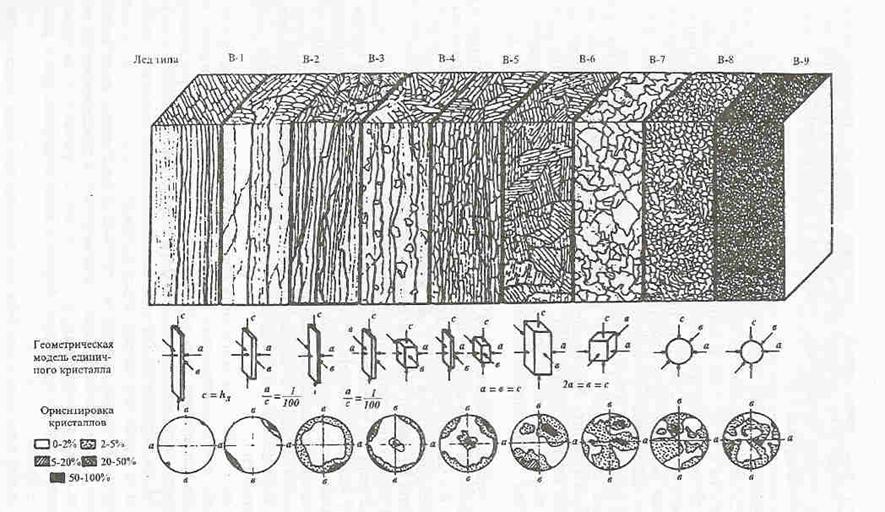
Рис. 1.2.Основные типы морских льдов (группа "В")

При определении пределов прочности льда с помощью соотношения (1.1) учет структуры льда осуществляется с помощью безразмерного коэффициента а. Значения этого коэффициента приведены в таблице 1.2.

Таблица 1.2

Значения коэффициента а, учитывающего структуру льда

Класс льда	Структура и тип льда	Значенияа для разных типов деформации
сжатие	изгиб	срез
Пресноводный	Призматическая А1, А2	1.5	1.6	-
Шестовато-игольчатая А3, А4	1.0	1.0	1.0
Зернистая А6, А7, А8, А9	0.5	0.5	-
Морской	Волокнистая крупноагрегатная В1	1.3	1.1	1.6
Волокнистая В2, В3, В4	1.0	1.0	1.0
Волокнистая В5	1.0	0.8	1.0
Зернистая В6, В7, В8, В9	0.5	0.5	0.9

Влияние плотности льда на его прочностные свойства описываются коэффициентом b, значения которого представлены в таблице 1.3.

Таблица 1.3

Значения коэффициента b, учитывающего плотность льда

Плотность льда, кг/м3	Значения b для разных типов деформации
Для воздушных полостей сферической формы	Для воздушных полостей цилиндрической формы
Сжатие и срез	Изгиб	Сжатие и срез	Изгиб
	1.0	1.0	1.0	1.0
	0.99	0.98	0.92	0.85
	0.97	0.95	0.86	0.76
	0.95	0.92	0.81	0.7
	0.91	0.87	0.73	0.59
	0.87	0.82	0.67	0.52

Значение коэффициента с, учитывающего влияние среды, окружающей образец, на его прочностные свойства не зависит от вида деформации образца. Величина этого коэффициента при проведении испытаний на воздухе равна 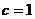, а при проведении испытаний в воде - .

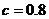Значения безразмерных коэффициентов d и f зависят от вида деформации образца, поэтому данные для нахождения этих коэффициентов будут приведены ниже при рассмотрении при рассмотрении методик расчета пределов прочности льда.

Расчет пределов прочности образцов льда при сжатии.

1. По семейству графиков, представленных на рис. 1.3, определяется 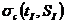при заданных температуре и солености льда.

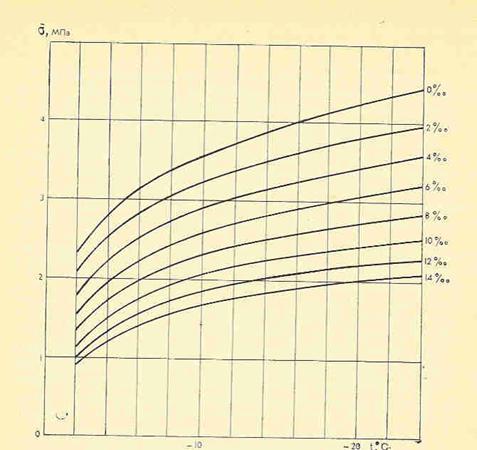
Рис. 5.3. Зависимость обобщенного предела прочности малых образцов льда на сжатие от его температуры и солености

2. Определяются значения поправочных коэффициентов в выражении (1.1). Значения коэффициентов a, b, cприведены в таблицах 1.2 и 1.3. Величины коэффициентов d и f определяются из таблицы 1.4 и рис.1.4.

Таблица 1.4

Значения коэффициента d, учитывающего направление приложения нагрузки относительно ориентации основных структурных элементов льда при сжатии и срезе.

Направление приложения нагрузки ко льду	Значения d
Перпендикулярно граням образца, параллельным поверхности ледяного покрова, из которого образец взят (вдоль длинных осей структурных элементов льда)	1.2
Параллельно граням образца, параллельным поверхности ледяного покрова, из которого образец взят (перпендикулярно длинным осям структурных элементов льда)	0.8
Параллельно или перпендикулярно граням образца, параллельным поверхности ледяного покрова, из которого образец взят (безразлично по отношению к структурным элементам изотропного льда). Для пресноводных и морских льдов зернистой структуры (А6, A7, A8, A9, B6, B7, B8, B9.	1.0

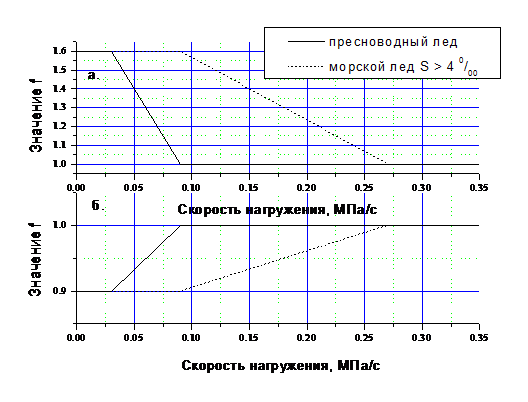
Рис.1.4. Значения коэффициента f, учитывающего скорость нагружения образцов при сжатии.

а. При приложении нагрузки вдоль структурных элементов льда;

б. При приложении нагрузки перпендикулярно структурным элементам льда.

Расчет предела прочности льда при изгибе.

1. По семейству графиков, представленных на рис. 1.5, определяется 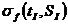при заданных температуре и солености льда. Балки для проведения испытаний выбирались из ледяного покрова таким образом, чтобы их длинные ребра были параллельны поверхности льда. Разрушение балки осуществлялось по двух опорной схеме, в которой нагрузка прикладывается в точке равноудаленной от опор.

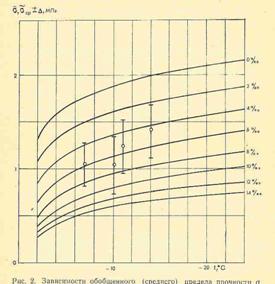
Рис. 1.5. Зависимости обобщенного предела прочности льда на изгиб от температуры льда и его солености.

2. Определяются значения поправочных коэффициентов в выражении (1.1). Значения коэффициентов a, b, c приведены в таблицах 1.2 и 1.3. Значение коэффициента d, учитывающего направление приложения нагрузки относительно ориентации основных структурных элементов балки для данных, приведенных на рис. 1.5, следует принимать равным 1. Значение коэффициента f по графику, представленному на рис.1.6.

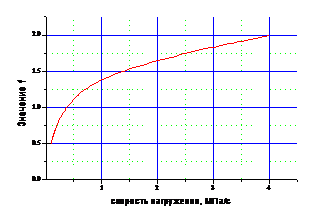
Рис. 5.6. Зависимость коэффициента f от скорости нагружения образца.

Расчет предела прочности при сдвиге.

1. По семейству графиков, представленных на рис. 1.7, определяется 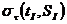при заданных температуре и солености льда.

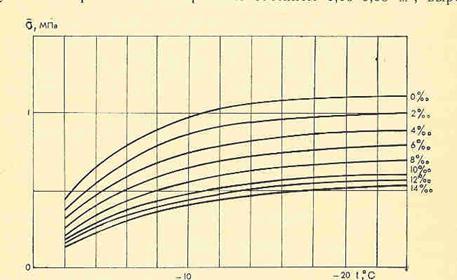
Рис. 5.7. Зависимости обобщенного предела прочности льда при срезе от температуры льда и его солености.

2. Определяются значения поправочных коэффициентов в выражении (1.1). Значения коэффициентов a, b, c и d приведены в таблицах 1.2, 1.3 и 1.4. Значение коэффициента f, учитывающего скорость возрастания нагрузки, следует принимать равным 1.

Исходные данные

Исходные данные для выполнения работы представлены в табл. 1.5., варианты 0 ¸ 9.

Таблица 1.5

Характеристика льда	Номер варианта
Тип льда	В1	В2	В3	В4	В5	В6	В7	В8	В9	А4
Диапазон изменения температуры льда, 0С	от –2 до –20 (шаг 2 0С)
Соленость льда, 0/00
Плотность льда, кг/м3
Форма воздушных включений	сф.	цил.	сф.	цил.	сф.	цил.	сф.	цил.	сф.	цил.
Среда, в которой проводятся истытания	возд.	вода	возд.	вода	возд	вода	возд	вода	возд	вода
Направление приложения нагрузки	;	^	;	^	;	^	;	^	;	^
Скорость приложения нагрузки, МПа/с	сжатие	0,1	0,11	0,12	0,13	0,14	0,15	0,2	0,28	0,27	0,04
изгиб	0,1	0,15	0,2	0,25	0,3	0,5			2,5	0,04
n

Пояснения к таблице:

- сф. – сферические, цил. – цилиндрические;возд. – воздух;

- ; - нагрузка приложена параллельно граням, параллельным поверхности ледяного покрова; ^ - нагрузка приложена перпендикулярно граням, параллельным поверхности ледяного покрова;

- n – число, которое показывает во сколько раз необходимо увеличить размер расчетного образца по сравнению с малым образцом.

Порядок выполнения работы

1. Рассчитать величины пределов прочности льда для заданного диапазона изменения температуры. Расчет выполняется на основании выражения (5.1). Значения поправочных коэффициентов определяются по приведенным в работе графикам и таблицам в соответствии с исходными данными.

2. Построить графики зависимости пределов прочности льда от температуры .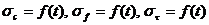

3. Строятся графики, иллюстрирующие взаимосвязь различных пределов прочности льда. Для построения этих графиков из зависимостей 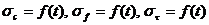исключается температура. В результате строятся два графика .

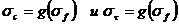Составление отчета

В отчет по лабораторной работе входят:

1. графики зависимостей , ;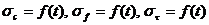

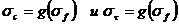2. анализ полученных результатов.

Расчетная работа № 2

Общие пояснения

При проектировании ледоколов и судов активного ледового плавания, а также при разработке различных морских транспортных систем, предназначенных для эксплуатации на замерзающих акваториях, одним из важнейших моментов является определение ледового сопротивления, испытываемого судном при движении во льдах. Многообразие наблюдаемых в реальных условиях различных ледовых образований не позволяет создать расчетные методы определения ледового сопротивления для всех них. Поэтому в морской ледотехнике принято определять ледовое сопротивление для так называемых эталонных ледовых условий. Принято считать, и это подтверждается практикой эксплуатации судов во льдах, что хорошие показатели ледовой ходкости проектируемого судна в эталонных условиях обеспечивают ему эффективность во всем многообразии ледовых условий. К эталонным ледовым условиям обычно относятся следующие: сплошной ровный ледяной покров, мелкобитый лед естественного или искусственного (канал за ледоколом) происхождения, торосистые образования, тертый лед в набитом канале или на акватории порта.

В настоящее время разработано довольно большое количество различных расчетных методов для определения ледового сопротивления судна. Все эти методы можно условно разбить на три большие группы: эмпирические, полуэмпирические и теоретические методы. К эмпирическим методам относятся методы, построенные исключительно на основании обработки данных натурных или модельных экспериментов. Как правило, при анализе таких методов крайне сложно понять, почему тот или иной значимый физический параметр включен в формулу именно таким, а не иным способом. В качестве примера можно привести эмпирическую формулу Л.Г.Цоя для определения предельнойледопроходимости судна.

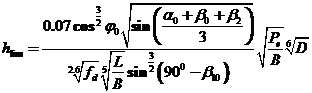, (2.1)

где 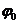- угол наклона форштевня к конструктивной ватерлинии (КВЛ); 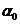- угол наклона носовой ветви ватерлинии к диаметральной плоскости на 0-ом теоретическом шпангоуте; 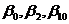- углы развала шпангоутов на 0-ом, 2-ом и 10-ом теоретических шпангоутах соответственно; 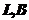- длина и ширина судна по КВЛ; 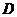- весовое водоизмещение судна, т; 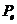- суммарная тяга гребных винтов на режиме, близком к швартовному, т; 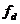- коэффициент динамического трения корпуса о лед.

Формула (2.1) получена на основе обработки данных модельных испытаний серии судов. Эта обработка позволила получить значения численных коэффициентов используемых в формуле. Роль подгоночного коэффициента играет также величина коэффициента трения. Автор рекомендует использовать следующие значения для этого коэффициента: 0.065 – для нержавеющей стали; 0.072 – для покрытия типа "Инерта – 160" и 0.08 для обычной судостроительной стали.

Опыт применения формулы Л.Г.Цоя показывает, что она достаточно хорошо предсказывает предельнуюледопроходимость ледоколов и судов, форма корпуса и главные размерения которых незначительно отличаются от исследованной серии моделей. Если эти параметры существенно отличаются от испытанных в модельном эксперименте, то ошибка может быть значительной. Выражение (2.1) может завышать предельную ледопроходимость крупнотоннажных судов, т.к. в ней содержится сильная зависимость этого параметра от весового водоизмещения.

Основу современного расчета ледового сопротивления судна составляют полуэмпирические и аналитические методы. Различие между ними довольно условное и заключается в большей или меньшей степени использования эмпирического материала. При выводе полуэмпирических формул используется упрощенная математическая модель изучаемого явления. Корреляция результатов расчетов по такой модели с экспериментальными данными достигается за счет введения поправочных коэффициентов, т.е. корректируется вся расчетная модель. В аналитических методах эмпирическая информация используется при разработке моделей физических явления, сопровождающих движение судна во льдах. Из совокупности таких моделей получается расчетный алгоритм, по которому проводятся расчеты.

Все математические модели, созданные для описания ледового сопротивления судна, содержат решение трех основных задач:

§ описание процессов, происходящих при движении ледокола во льдах;

§ определение критериев разрушения ледового покрова и описание картины его разрушения;

§ описание формы поверхности корпуса судна в районе его взаимодействия со льдом.

Уточнение решения указанных задач составляет суть развития методов расчета ледового сопротивления.

Определение ледового сопротивления обычно не является окончательной целью проведения расчетов или экспериментальных исследований. Для праектантовважное значение имеют показатели ледовой ходкости судов. Ледовая ходкость определяется, как возможность судна преодолевать ледовый покров определенной толщины с определенной скоростью, которая задается мощностью главных механизмов. Это понятие, как и в случае движения судна на чистой воде, включает в себя, две составляющие: сопротивление льда движению судна и пропульсивные качества движительного комплекса в ледовых условиях. Основными характеристиками ледовой ходкости являются ледопроходимость, а также кривая ледопроходимости. Под ледопроходимостью понимают предельную толщину сплошного ровного льда, которую может преодолеть судно ледового плавания, двигаясь с минимальной устойчивой скоростью при работе энергетической установки на полную мощность. В качестве минимальной устойчивой скорости обычно принимается скорость движения равная 1,5 – 2 узлам. Кривая ледопроходимости представляет собой зависимость скорости движения судна от толщины преодолеваемого им льда при постоянном значении мощности энергетической установки. Типичный вид кривой ледопроходимости представлен на рис.2.1.

Для получения кривой ледопроходимости необходимо иметь информацию о зависимости ледового сопротивления и тяги движительного комплекса от скорости движения судна. При этом ледовое сопротивление определяется при различных значениях толщины льда. Указанные зависимости наносятся на один график и определяются точки пересечения кривых ледового сопротивления с кривой тяги. По этим точка затем строится кривая ледопроходимости.

Из приведенных выше определений следует, что для определения ледопроходимости судна необходимо уметь определять как его ледовое сопротивление в различных ледовых условиях, так и тягу движительного комплекса в этих же условиях.

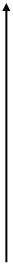
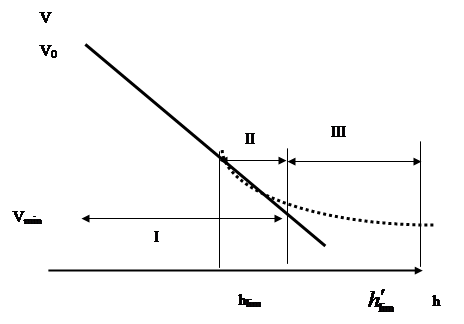Рис. 2.1 Типичный вид кривой ледопроходимости.

V₀ – скорость судна на чистой воде; V_min – минимальная устойчивая скорость движения судна во льдах; h_lim – предельная толщина ровного льда, преодолеваемого судном непрерывным ходом (предельная ледопроходимость); 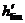-предельная толщина льда, преодолеваемого судном при движении набегами.

Зона I – судно движется непрерывным ходом в сплошных льдах. Зона II – судно может двигаться непрерывным ходом с небольшой скоростью, либо работать набегами. Зона III – судно может двигаться, работая только набегами.

Ниже будут рассмотрены часто применяемые в настоящее время полуэмпирические формулы для расчета ледового сопротивления, принадлежащие Б.П. Ионову и А.Я.Рывлину. Формула Б.П. Ионова позволяет определить сопротивление судна при его движении в сплошных ровных льдах. Эта формула будет приведена в несколько измененном виде. Изменения касаются последнего слагаемого, входящего в формулу, которое учитывает сопротивление цилиндрической вставки. Для современных крупнотоннажных судов, имеющих цилиндрическую вставку с прямыми бортами, расчет этой составляющей сопротивления осуществляется по методике, предложенной автором этого пособия.

Формула А.Я. Рывлина позволяет рассчитать ледовое сопротивление судна при его движении в битых льдах. Эта формула будет приведена также с изменениями, выполненными автором пособия. Эти изменения касаются перевода формулы из технической метрической системы в систему СИ, аппроксимации графиков, которые используются для расчетов, и расширения использования формулы для больших значений углов входа ватерлинии.

Методика выполнения работы

Аналитическое определение формы ватерлинии и углов наклона шпангоутов

Для выполнения расчетов ледового сопротивления необходимо иметь информацию о форме носовой оконечности судна, включая цилиндрическую вставку, на уровне действующей ватерлинии. При расчетах проектируемого судна эта информация снимается с теоретического чертежа. Для удобства выполнения расчетной работы ниже приводятся формулы для аналитического описания формы ватерлинии судна ледового плавания.

Обобщенно форма для носовой ветви ватерлиниипроизвольного ледокольного судна в системе координат OXY, где начало координат совпадает с миделевым сечением, ось OX направлена в нос, а ось OY на правый борт, может быть задана следующим образом:

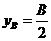при х < 0,5L_PM

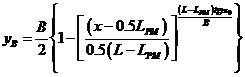при 0,5L³x³ 0,5L_PM, (2.2)

где 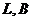- длина и ширина судна; 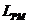- длина цилиндрической вставки; 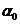- угол входа носовой ветви ватерлинии.

Распределение углов наклона шпангоутов для носовой ветви ватерлинии задается следующим выражением:

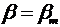при х < 0,5L_PM

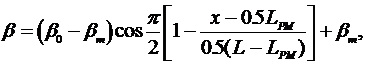при 0,5L³x³ 0,5L_PM(2.3)

где 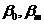- углы наклона нулевого шпангоута и шпангоута на миделе.

Угол наклона нулевого шпангоута может быть рассчитан по следующей формуле:

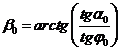, (2.4)

где 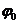- угол наклона форштевня.

Метод расчета ледового сопротивления с сплошных льдах

В соответствии с методом, предложенным Б.П.Ионовым, расчет ледового сопротивления судна в сплошных льдах выполняется по следующим формулам:

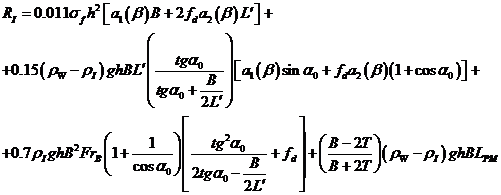(2.5)

здесь 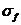- предел прочности льда на изгиб; 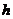- толщина льда; 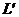- длина носового заострения; 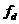-динамический коэффициент трения льда об обшивку корпуса; 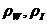- плотность воды и льда; 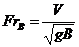- число Фруда, вычисленное по ширине корпуса судна; 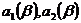специальные функции формы корпуса судна, зависящие от распределения углов наклона шпангоутов по длине носового заострения, определяемые следующими выражениями:

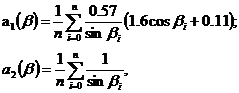(2.6)

где 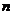число шпангоутов в пределах носового заострения, которые используются для определения функций формы; 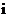- текущий номер шпангоута. При небольшой длине носового заострения судна для более точного описания зависимостей 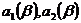рекомендуется определять углы наклона шпангоутов с шагом ½ или ¼ теоретической шпации. При вычислении выражений (2.6) углы наклона шпангоутов 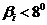не учитываются.

В случае, если угол наклона шпангоутов цилиндрической вставки 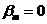вместо последнего слагаемого в формуле (2.5) необходимо использовать выражение:

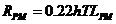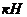, (2.7)

гдеТ – осадка судна.

Примечание: При использовании формул (2.5) – (2.7) необходимо следить за размерностью используемых величин. Если прочность льда на изгиб принимается в МПа, плотность воды и льда должна измеряться в кт/м³, тогда результат расчета будет получен в МН. Если прочность измеряется в кПа, то, соответственно плотность в т/м³ и результат в кН. И наконец, прочность в Па, плотность в кг/м³, результат в Н. При выполнении расчетов по формуле (2.7) в случае использования прочности льда на изгиб в МПа или в Па необходимо соответствующим образом изменить численный коэффициент 0.22.

Метод расчета сопротивления судна в мелкобитых льдах

Для оценок сопротивления битого льда наиболее часто используется полуэмпирическая формула, предложенная А.Я.Рывлиным:

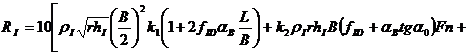(2.8)

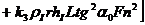
где 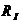- чистое ледовое сопротивление, т.е. сопротивление битого льда определенное без учета сопротивления воды; r – характерный размер мелкобитого льда, м; h_I – толщина мелко битого льда, м; r_I – плотность льда, кг/м³; f_ID – коэффициент трения льда об обшивку корпуса; L - длина судна; В – ширина судна; a_В – коэффициент полноты носовой ветви ватерлинии, который равен

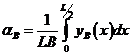, (2.9)

здесь 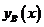задается формулой (2.2) (интеграл студенты вычисляют самостоятельно); a₀ – угол наклона носовой ветви ватерлинии к диаметральной плоскости, град; Fn – число Фруда; k₁,k₂,k₃ – безразмерные эмпирические коэффициента, выбираемые в зависимости от сплоченности льда (см. таблицу 2.1).

Таблица 2.1.

Значения эмпирических коэффициентов в формуле (2.8)

Сплоченность, баллы
k1×102
k2			2.8	5.1	8.5
k3	4.2	4.2	4.2	4.2	4.2

При проведении расчетов удобнее пользоваться следующими аппроксимационными формулами:

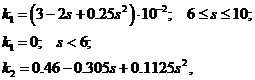(2.10)

где 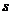- сплоченность мелкобитого льда в баллах.

Среднестатистическое значение параметра rh для природных льдов сравнительно стабильно. В среднем оно равно приблизительно 4 м². При движении по каналам, проложенным ледоколом в сплошных ровных льдах, величина параметра rh может быть определена по формуле:

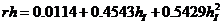. (2.11)

При применении формулы (2.8) к судам, имеющим угол наклона носовой ветви ватерлинии к диаметральной плоскости больший чем 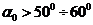, встречает некоторые затруднения, связанные с тем, что 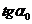принимает не реально большие значения. Обойти их можно следующим образом. При движении такого тела в мелкобитом льду, например, при буксировке имеющего прямоугольную форму инженерного сооружения, перед его носом формируется зона льда, имеющая треугольную форму в плане, которая буксируется вместе с телом. Протяженность этой зоны можно приблизительно рассчитать по следующей формуле:

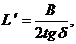(2.12)

здесь В – характерный поперечный размер движущегося в битых льдах или буксируемого в них тела, d ≈45⁰- угол внутреннего трения битого льда, как сыпучей среды.

Наиболее часто суда движутся в мелкобитом льду, который образовался после прокладки ледоколом канала в различных ледовых условиях. При движении судов по ледяным каналам необходимо различать два возможных их состояния: свежий канал и старый набитый канал. На рис. 2.2 представлены поперечные сечения свежего и старого каналов. Свежий канал образуется сразу же после прохождения ледокола. Старый канал формируется после многократного прохождения по нему судов. Такой канал в основном заполнен тертым льдом.

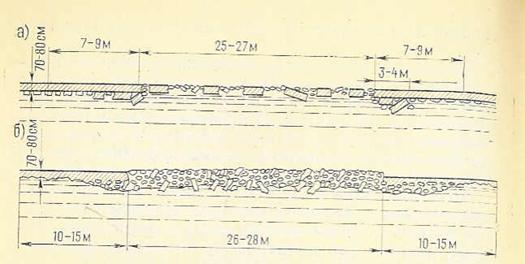
Ри.2.2 - Вид поперечного сечения свежего (а) и старого (б) каналов в припае в зимний период года

Для расчета сопротивления судна при движении по свежему каналу можно использовать формулы (2.8) – (2.12). В этом случае коэффициент 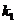зависит от относительной ширины проложенного ледоколом канала 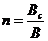, где 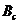- ширина канала, 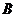- ширина судна. Зависимость коэффициента