Расчёт статически неопределимых систем методом сил на температурное и кинематическое воздействие

Лекция семнадцатая

Расчёт статически неопределимых систем методом сил на температурное и кинематическое воздействие

17.1. Расчёт стержневых статически неопределимых систем на температурное воздействие

17.2. Пример расчёта статически неопределимой рамы на температурное воздействие в обычной форме

17.3. Пример расчёта статически неопределимой рамы на температурное воздействие в матричной форме

17.4. Расчёт стержневых статически неопределимых систем на кинематическое воздействие

17.5. Пример расчёта статически неопределимой рамы на смещение опорных связей в обычной форме

17.6. Пример расчёта статически неопределимой рамы на смещение опорных связей в матричной форме

17.7. Вопросы для самопроверки

17.8. Рекомендуемая литература

Пример расчёта статически неопределимой рамы на температурное воздействие в обычной форме

Со стороны внутренних волокон стержней левого контура рамы (рис. 17.2,а) температура повысилась на 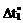= 30 °С, со стороны наружных волокон левой стойки и верхних волокон ригеля температура понизилась на 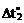= -50 °С. Поперечные сечения элементов рамы прямоугольные размером b´h (h = 0,2 м). Коэффициент линейного температурного расширения материала, из которого изготовлены стержни рамы, известен и равен a. Требуется построить эпюры внутренних усилий от заданного температурного воздействия.

1. Определение степени статической неопределимости рамы:

n_st = 3К – Н = 3 × 2 – 5 = 1.

2. Выбор статически определимой основной системы метода сил. Лишнюю связь заданной рамы удалим путём введения цилиндрического шарнира в её верхний левый узел (рис. 17.2,б). Читателям предлагается произвести кинематический анализ полученной основной системы и убедиться в её геометрической неизменяемости.

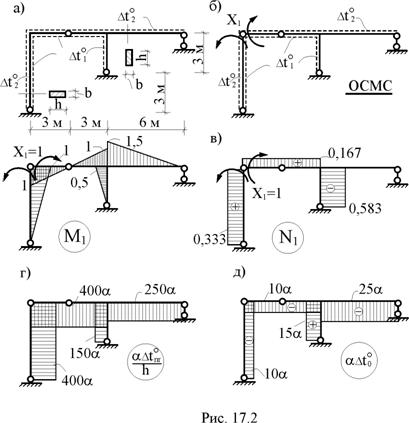
3. Построение эпюры изгибающих моментов М₁ и эпюры продольных сил N₁ в основной системе от Х₁ = 1 (рис. 17.2,в).

4. Построение условных эпюр, связанных с перепадами приращений температур по высоте поперечного сечения 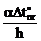и приращениями температур на уровне центров тяжести поперечных сечений 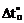(рис. 17.2,г,д). При построении этих эпюр учтено, что h = 0,2 м, и приняты во внимание следующие численные значения величин 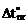и :

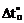– для левого ригеля и левой стойки:

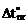= 30 – (–50) = 80 °С, 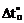= = 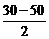–10 °С;

– для правого ригеля:

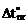= 0 – (–50) = 50 °С, 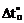= = 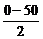–25 °С;

– для правой стойки:

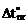= 30 – 0 = 30 °С, 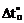= = 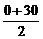15 °С.

Ординаты эпюры 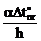отложены со стороны более "тёплых" волокон, на эпюре же a 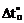зафиксирован знак "плюс" на элементах с положительными приращениями температур на уровне центров тяжести поперечных сечений и знак "минус" – с отрицательными (см. п. 12.2 и пример 12.2.1 второй части настоящего курса лекций).

5. Вычисление коэффициентов разрешающего уравнения метода сил

d₁₁Х₁ + D_1t = 0. (17.1,а)

Как и при силовом воздействии, в рамных системах коэффициент d₁₁ вычисляется без учёта влияния на величину искомого перемещения деформаций сдвига и растяжения–сжатия.

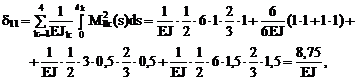
где .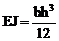

Перемещение по направлению Х₁ от заданного изменения температуры в основной системе определим по формуле (17.2), вычисляя определённые интегралы сопряжением эпюры М₁ с эпюрой 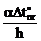и эпюры N₁ с эпюрой a .

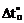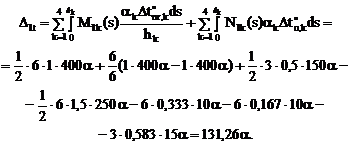
6. Вычисление неизвестного метода сил из уравнения (17.1,а):

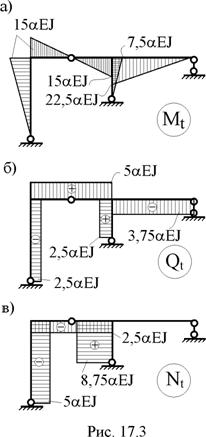
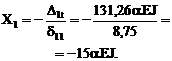
7. Определение изгибающих моментов в сечениях заданной рамы от температурного воздействия и построение эпюры M_t (рис. 17.3,а). Из первого выражения соотношений (17.3) имеем:

M_t = M₁ X₁,

где Х₁ = –15aEJ.

8. Кинематическая проверка решения задачи. Для этой проверки используем формулу (17.4), в которой сохраним только первый член, ибо коэффициент d₁₁ выше нами был определён только с учётом деформаций изгиба.

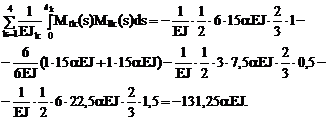
Результат сопряжения эпюр M_t и М₁ практически совпал с численным значением правой части разрешающего уравнения (17.1,а)

d₁₁ X₁ = –D_1t,

что подтверждает правильность решения поставленной задачи.

9. Построение обычным порядком эпюры поперечных сил Q_t (рис. 17.3,б) и эпюры продольных сил N_t (рис. 17.3,в). В нашей задаче окончательную эпюру продольных сил N_t можно также получить, используя последнее выражение соотношения (17.3), которое для рассматриваемой задачи примет вид:

N_t = N₁ Х₁.

Обращаем внимание читателя на то, что ординаты окончательных эпюр внутренних усилий (М_t, Q_t, N_t) зависят от абсолютного значения изгибной жёсткости поперечного сечения элементов рамы EJ.

Пример расчёта статически неопределимой рамы на температурное воздействие в матричной форме

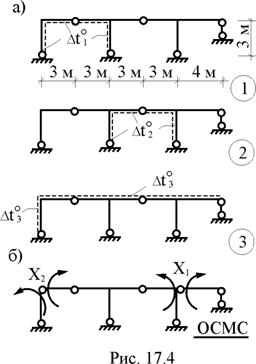В статически неопределимой раме (рис. 17.4,а) возможны следующие независимые друг от друга варианты температурных воздействий: первый – повышение температуры со стороны внутренних волокон стержней левого контура на = 120 °С, второй – повышение температуры со стороны внутренних волокон элементов среднего контура на 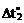= 80 °С, третий – понижение температуры со стороны наружных волокон левой стойки и ригелей на 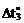= –40 °С. Ширина прямоугольных поперечных сечений стоек и ригелей рамы одинакова и равна b; высота поперечного сечения стойки h_c = h, ригеля – h_p = 1,587h (h = 0,3 м). Коэффициент линейного температурного расширения материала, из которого изготовлены элементы рамы, равен a. Требуется построить эпюры внутренних усилий в заданной раме от каждого из вышеперечисленных вариантов температурных воздействий.

Размеры прямоугольных поперечных сечений рамы заданы так, что сохраняется соотношение изгибных жесткостей поперечных сечений ригелей и стоек, принятое для расчёта этой же рамы, в матричной форме на силовое воздействие в п. 16.8 шестнадцатой лекции, а именно: EJ_p : EJ_c = 2 : 0,5. Приняв EJ_p = 2 EJ, EJ_с = 0,5 EJ, получим численное значение жесткостного параметра EJ:

.

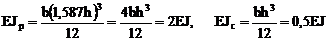Каждое из этих соотношений даёт

.

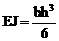Для расчёта рамы на температурное воздействие в матричной форме используем соотношение (17.10), в котором примем L = M, B = B_M, S_t = M_t, так как вычисление матрицы внешней жёсткости принятой основной системы метода сил (рис. 17.4,б) будем производить только с учётом изгибных деформаций. В этом случае матричное выражение (17.10) перепишется:

M_t = –M(M^T B_M M)^-1 (L^T_t B_t T).

1. Определение степени статической неопределимости рамы и выбор основной системы метода сил (рис. 17.4,б). Основная система для расчёта рамы на температурное воздействие будет такой же, как и при её расчёте на силовое воздействие в матричной форме (см. п. 16.8 шестнадцатой лекции).

2. Построение эпюр изгибающих моментов и продольных сил в основной системе метода сил от Х₁ = 1 и Х₂ = 1 (рис. 17.5,а). Эпюры изгибающих моментов М₁ и М₂ от этих воздействий были получены ранее (см. п. 16.8, рис. 16.14,в,г).

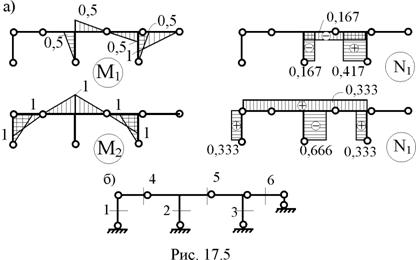
3. Формирование матрицы изгибающих моментов М от Х₁ = 1 и Х₂ = 1 в основной системе и матрицы внутренней упругой податливости В_М в соответствии с принятой на рис. 16.16 нумерацией грузовых участков и сечений (см. п. 16.8 шестнадцатой лекции).

5. Вычисление элементов матрицы внешней податливости принятой для расчёта основной системы метода сил (см. п. 16.8 шестнадцатой лекции).

.

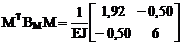6. Обращение матрицы внешней податливости рамы (см. п. 16.8 шестнадцатой лекции).

.

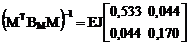7. Нумерация участков и сечений для формирования матрицы изгибающих моментов и продольных сил от Х₁ = 1, Х₂ = 1 в основной системе L_t, матрицы температурной податливости сооружения B_t и матрицы приращений температур Т (рис. 17.5,б). Заметим, что при расчёте рамы на температурное воздействие номера участков и их срединных сечений совпадают.

8. Формирование матрицы L_t по эпюрам внутренних усилий M₁, N₁, M₂, N₂ (рис. 17.5,а) в соответствии с принятой нумерацией срединных сечений.

9. Формирование матрицы температурной податливости сооружения B­_t в соответствии с принятой нумерацией участков (рис. 17.5,б).

,

где ,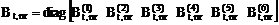

;

.

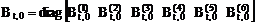
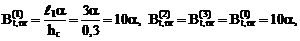
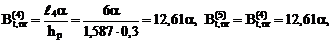
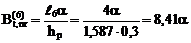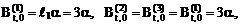
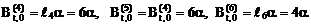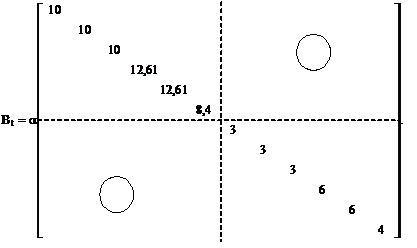
10. Построение эпюр неравномерных (T_nr) и равномерных приращений температур (Т₀) по вариантам воздействий (рис. 17.6).

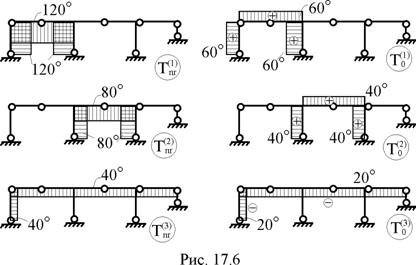
Ординатами этих эпюр (соответственно, и элементами матриц T_nr и T₀) на k-том участке являются перепад приращений температур по высоте поперечного сечения 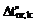и приращение температуры в центре тяжести поперечного сечения . Численное значение величин 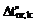и по вариантам воздействий читателям предлагается получить самостоятельно.

11. Формирование матрицы приращений температур Т по вариантам воздействий (рис. 17.6) в соответствии с принятой нумерацией участков. Правило знаков для элементов матрицы T_nr совпадает с правилом знаков для элементов матрицы М (см. пример 13.4.1 тринадцатой лекции). Знаки элементов подматрицы Т₀ совпадает со знаком приращений температуры в центрах тяжести поперечных сечений , т.е. со знаками эпюры Т₀ на рассматриваемых участках.

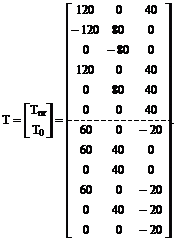
12. Вычисление элементов матрицы свободных членов системы канонических уравнений по вариантам воздействий

.

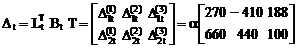13. Определение матрицы неизвестных метода сил по вариантам температурных воздействий.

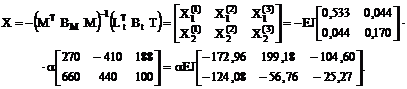
14. Вычисление элементов матрицы изгибающих моментов M_t в заданной раме и построение соответствующих эпюр по вариантам температурных воздействий (рис. 17.7) в соответствии с принятой нумерацией участков и сечений (рис. 16.16).

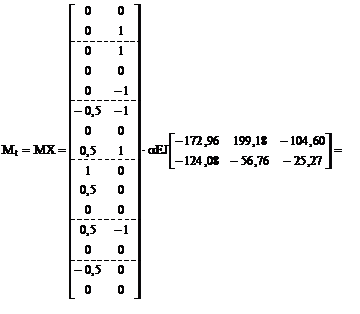
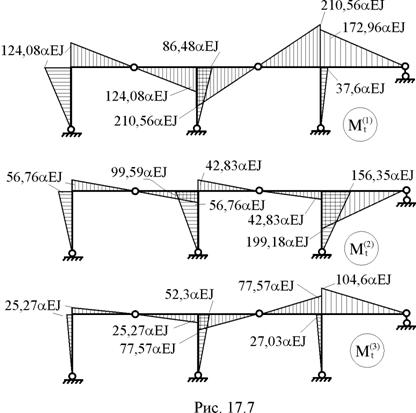
15. Кинематическая проверка. Используя матричное соотношение (17.11), в котором для нашей задачи L = M, B = B_M, S_t = M_t, мы должны получить матрицу свободных членов системы канонических уравнений по вариантам температурных воздействий с обратным знаком, т.е.

M^T B_M M_t = –D_t.

После подстановки в последнее соотношение матриц М, В_М и M_t получим:

M^T B_M M_t = .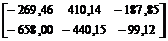

Элементы вычисленной матрицы по абсолютной величине соответствуют элементам матрицы D_t, полученной выше, с относительной погрешностью, не превышающей 0,9 %.

16. Построение по вариантам температурных воздействий эпюр поперечных сил Q_t по эпюрам М_t и эпюр продольных сил N_t по эпюрам Q_t. Читателям предлагается построение этих эпюр выполнить самостоятельно.

Пример расчёта статически неопределимой рамы на смещение опорных связей в обычной форме

В раме, показанной на рис. 17.9,а, горизонтальная связь левой опоры получила перемещение влево на D₍₁₎ = 2 см, вертикальная связь этой же опоры – вниз на D₍₂₎ = 1 см. Изгибная жёсткость поперечных сечений стержней рамы известна и равна постоянной величине EJ. Требуется построить эпюры внутренних усилий от заданного смещения опорных связей.

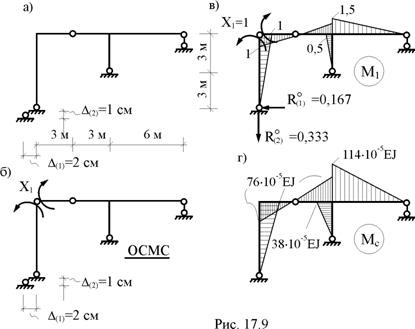
В п. 17.2 эта же рама была рассчитана на температурное воздействие. Некоторыми результатами этого расчета воспользуемся в рассматриваемом примере.

1. Определение степени статической неопределимости и выбор статически определимой основной системы метода сил (см. п. 17.2, рис. 17.9,б).

2. Построение эпюры изгибающих моментов М₁ и вычисление реакций в смещаемых связях 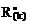в основной системе от Х₁ = 1 (рис. 17.9,в).

3. Вычисление коэффициентов разрешающего уравнения метода сил

d₁₁ Х₁ + D_1с = 0.

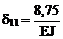(см. п. 17.2).

Перемещение по направлению Х₁ от заданного смещения опорных связей определим по формуле (17.13).

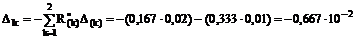(рад).

4. Решение уравнения метода сил:

.

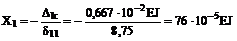5. Определение изгибающих моментов в характерных сечениях рамы от заданных смещений горизонтальной и вертикальной связей левой опоры и построение эпюры М_с (рис. 17.9,г). Из первого выражения группы соотношений (17.14) следует:

M_c = M₁X₁, где X₁ = 76 × 10^-5EJ.

6. Кинематическая проверка эпюры М_с по формуле (17.15). В этой формуле сохраним только первый член, учитывающий изгибные деформации элементов рамы.

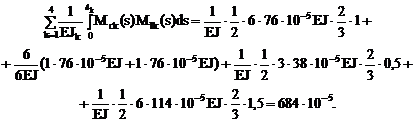
Результат сопряжения эпюр М_с и М₁ совпадает с численным значением правой части разрешающего уравнения метода сил d₁₁Х₁ = –D_1с = –(-0,667×10^-2) = 667×10^-5 с относительной погрешностью вычислений:

e = 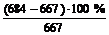= 2,55 %,

что подтверждает правильность вычисления ординат эпюры М_с.

7. Построение эпюры поперечных сил Q_c по эпюре изгибающих моментов М_с и эпюры продольных сил N_c по эпюре Q_c. Читателям предлагается самостоятельно выполнить построение эпюр Q_c и N_c.

Пример расчёта статически неопределимой рамы на смещение опорных связей в матричной форме

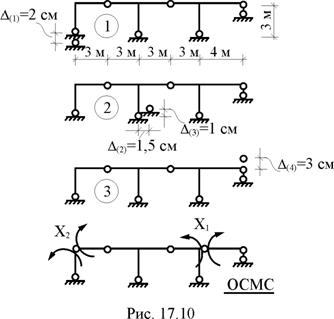
В раме, показанной на рис. 17.10, возможны следующие независимые друг от друга кинематические воздействия: первое – перемещение вертикальной связи левой опоры вниз на D₍₁₎ = 2 см, второе – перемещение горизонтальной связи вправо на D₍₂₎ = 1,5 см и вертикальной вверх на D₍₃₎ = 1 см опоры центральной стойки, третье – перемещение правой опоры вверх на D₍₄₎ = 3 см. Численные значения изгибных жесткостей поперечных сечений ригеля EJ_p и стоек EJ_с рамы заданы: EJ_p = 2 EJ, EJ_с = 0,5 EJ (EJ – известное число). Требуется вычислить элементы матрицы изгибающих моментов М_с для характерных сечений заданной рамы от каждого из вышеперечисленных кинематических воздействий.

Для расчёта рамы в матричной форме с учётом только изгибных деформаций её элементов используем соотношение (17.21). В этом случае L = М, В = В_М, S_c = M_c и матричное выражение (17.21) примет вид:

.

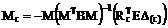В дальнейшем воспользуемся некоторыми результатами расчёта этой же рамы на силовое воздействие (см. п. 16.8 шестнадцатой лекции).

1. Выбор основной системы метода сил (рис. 16.14,б, рис. 17.10), построение в ней эпюр изгибающих моментов от Х₁ = 1, Х₂ = 1 (рис. 16.14,в,г), нумерация участков и сечений (рис. 16.16), формирование матриц изгибающих моментов в основной системе от Х₁ = 1, Х₂ = 1 и внутренней упругой податливости рамы М и В_М, вычисление элементов матрицы внешней податливости d = М^Т В_М М, обращение этой матрицы.

Примечание. Для расчёта рамы на температурное воздействие (см. п. 17.3) и в настоящем примере количество сечений на грузовых участках ригеля сохранено таким же, как и при расчёте рамы на силовое воздействие (рис. 16.16). Это обусловлено тем, что расчёт статически неопределимых систем на температурные и кинематические воздействия с помощью вычислительной техники производится вместе с расчётом на силовое воздействие. В частности, на кафедре строительной механике НГАСУ для расчёта статически неопределимых систем методом сил на все виды независимых друг от друга воздействий (силовые, температурные и кинематические) используется программа "Mefor", разработанная профессором В.Г. Себешевым.

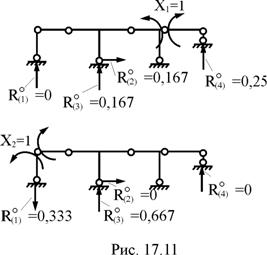
2. Формирование матрицы реакций в связях, получивших перемещение, от Х₁ = 1, Х₂ = 1 в основной системе (рис. 17.11).

.

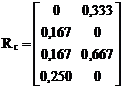В первой строке этой матрицы сначала от Х₁ = 1 (первый столбец), затем от Х₂ = 1 (второй столбец), зафиксированы реакции вертикальной связи левой опоры, во второй – реакции горизонтальной связи опоры центральной стойки, в третьей – вертикальной связи опоры центральной стойки, в четвёртой – правой опорной связи. Напоминаем, что реакция в смещаемой связи вносится в матрицу R_c со знаком "плюс", если её направление совпадает с направлением смещения связи, и со знаком "минус", – если не совпадает.

3. Составление матрицы величин перемещений опорных связей (в м) по вариантам воздействий.

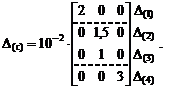
4. Вычисление матрицы перемещений по направлениям Х₁ и Х₂ от заданных кинематических возмущений в основной системе, или матрицы свободных членов системы канонических уравнений (17.16).

D_с = =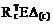

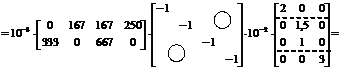
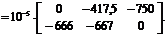
5. Определение элементов матрицы неизвестных метода сил.

X = –d^-1D_c = –(M^T B_M M)^-1 (R_c E D­_(c)) =

=

.

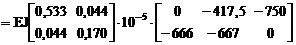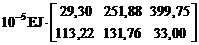6. Получение матрицы изгибающих моментов М_с в заданной раме по вариантам кинематических воздействий (рис. 17.10) в соответствии с принятой нумерацией участков и сечений (рис. 16.16).

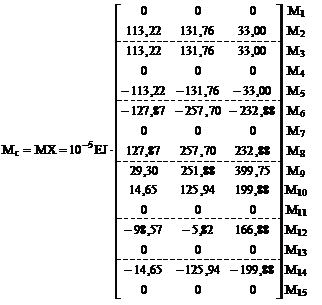
Читателям предлагается (используя соотношение (17.22), самостоятельно произвести кинематическую проверку правильности вычисления элементов матрицы М_с и построить для заданной рамы сначала эпюры изгибающих моментов, а затем и эпюры поперечных и продольных сил от упомянутых выше смещений опорных связей.

Вопросы для самопроверки

1. Задана статически неопределимая система (балка, рама, ферма или комбинированная система). Требуется произвести её расчёт на конкретное температурное или кинематическое воздействие. Определите степень статической неопределимости системы, выберите один из вариантов статически определимой основной системы и запишите в общем виде систему канонических уравнений метода сил для расчёта сооружения на заданное воздействие. Какой смысл имеет i-я строка системы канонических уравнений? Поясните смысл коэффициентов D_it и D_ic этой системы уравнений. Запишите формулы для определения этих коэффициентов. Что означают параметры M_ik(s), a_k, h_k, 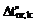, N_ik(s), , , 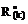D_(k), входящие в эти формулы?

2. Как определяются внутренние усилия в заданном статически неопределимом сооружении от температурных или кинематических воздействий, если известны усилия в лишних связях X₁, X₂, …, X_j, …, X_n?

3. Как производится проверка правильности эпюр внутренних усилий, полученных для заданного сооружения от температурных или кинематических воздействий?

4. Почему усилия в лишних связях X₁, X₂, …, X_j, …, X_n и ординаты эпюр внутренних усилий в статически неопределимом сооружении при его расчёте на температурные или кинематические воздействия зависят от абсолютного значения жесткостей поперечных сечений элементов сооружения?

5. Задано статически неопределимое сооружение, подверженное f независимым друг от друга температурным воздействиям или n, также независимым друг от друга, кинематическим воздействиям. Запишите в общем виде в матричной форме систему канонических уравнений метода сил для расчёта этого сооружения на температурные или кинематические воздействия. Сколько строк и столбцов содержится в матрицах D_t и D_с записанной системы уравнений?

6. Запишите матричные соотношения, используемые при расчёте статически неопределимых сооружений в случае температурных или кинематических воздействий:

а) для получения элементов матриц свободных членов D_t и D_с системы канонических уравнений метода сил;

б) для получения элементов матрицы неизвестных метода сил Х;

в) для определения элементов матриц внутренних усилий S_t или S_с для характерных сечений заданного сооружения.

7. Какую структуру имеют матрицы L_t, B_t, T, входящие в перечисленные в 6 вопросе матричные соотношения? Сколько строк и столбцов имеют матрицы L_t, B_t, T?

8. Поясните смыл элементов подматриц 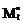, , 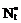B_t,nr, B_t,0, T_nr, T₀, а также матриц R_c, E, D_(c).

9. Сколько строк и столбцов имеют матрицы R_c, E, D_(c), если суммарное число смещаемых связей во всех n комбинациях кинематических воздействий равно e?

10. Сформулируйте правила знаков, используемых при формировании матриц L_t, T, R_c.

11. Как вычисляются элементы подматриц B_t,nr и B_t,0 матрицы температурной податливости сооружения B_t?

12. Каким образом в матричной форме производится кинематическая проверка правильности расчёта статически неопределимого сооружения на температурное или кинематическое воздействие? Запишите соответствующее матричное соотношение.

13. Поясните смысл следующих матричных выражений, используемых для расчёта статически неопределимых систем на температурное или кинематическое воздействие:

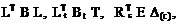
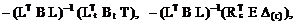
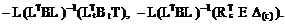
14. Какой смысл имеют элементы матрицы L? Сколько строк и столбцов имеет эта матрица? Как формируется матрица внутренней податливости сооружения В? Из каких блоков она состоит? Какой размер имеет эта матрица?

15. Какие блоки можно исключить из матриц L и В в случае, когда производится расчёт статически неопределимых рам и балок на температурные и кинематические воздействия.

16. Перепишите матричные соотношения, приведенные в п. 13, для расчёта статически неопределимых шарнирно-стержневых систем (ферм) на температурные и кинематические воздействия. Какой смысл в этом случае будут иметь элементы матриц L и L_t? Каким образом будут вычисляться элементы матриц В и B_t для шарнирно-стержневых систем?

17.8. Рекомендуемая литература

1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с.

Гл. 6. Метод сил. § 6.6. Расчёт статически неопределимых систем на действие температуры и осадки опор. – С. 134–136. § 6.7. Пример расчёта статически неопределимой рамы методом сил. – С. 140–142.

2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дар­ков, Н.Н. Шапошников. – М.: Высш. школа, 1986. – 607 с.

Гл. 6. Расчёт статически неопределимых систем методом сил. § 6.4. Расчёт статически неопределимых систем на действие температуры. § 6.5. Составление канонических уравнений при расчёте систем на перемещения опор. – С. 213–219.

3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащени­ков, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.

Гл. XI. Метод сил. § 63. Некоторые свойства статически неопределимых систем. Расчёт на действие температуры и осадку опор. – С. 361–368.

4. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики. Статика стержневых систем: Учеб. пособие / Г.К. Клейн, Н.Н. Леонтьев. – М.: Высш. школа, 1980. – 384 с.

Гл. IX. Расчёт рам методом сил. § IX.4. Расчёт рам на тепловое воздействие и смещение опор. – С. 162–166.

5. Анохин Н.Н. Строительная механика в примерах и задачах. Ч. 2. Статически неопределимые системы: Учеб. пособие / Н.Н. Анохин. – М.: Изд-во ассоциации строительных вузов, 2000. – 464 с.

Гл. 5. Расчёт сооружений методом сил. § 5.3. Тепловое воздействие. – С. 57–65. § 5.4. Кинематическое воздействие. – С. 69–75.

Лекция восемнадцатая

Предварительные замечания

Расчёт статически неопределимого сооружения на любые воздействия с математической точки зрения сводится к решению системы линейных алгебраических неоднородных уравнений, число неизвестных которой равно степени статической неопределимости сооружения. Решение этой системы уравнений требует большого объёма времени, особенно в расчётах сооружений с высокой степенью статической неопределимости. Сократить время решения системы канонических уравнений, составленной для расчёта заданного сооружения, можно выбирая основную систему метода сил так, чтобы возможно большее число побочных коэффициентов при неизвестных d_ij приняли нулевое значение. В этом случае система уравнений будет неполной, а в случае, когда все побочные коэффициенты d_ij равны нулю, она распадается на отдельные уравнения, каждое из которых содержит только одно неизвестное.

Принципиально такого рода задача может быть решена соответствующим выбором основной системы и неизвестных метода сил для любого статически неопределимого сооружения. Наиболее же просто она решается для сооружений, геометрия которых и распределение жесткостей поперечных сечений элементов, обладает хотя бы одной осью симметрии. Расчёт такого рода сооружений целесообразно проводить, используя симметричную основную систему метода сил (см. п. 18.2 и 18.3 настоящей лекции).

Вопросы для самопроверки

1. За счёт чего может быть произведено упрощение системы канонических уравнений метода сил при расчёте на произвольное внешние воздействие (силовое, температурное, кинематическое) статически неопределимых систем, имеющих хотя бы одну ось симметрии?

2. При каких условиях произойдёт разложение системы канонических уравнений метода сил на две независимые друг от друга системы уравнений? Какой характер имеют неизвестные метода сил, содержащиеся в каждой из этих систем уравнений?

3. Задана симметричная статически неопределимая система (балка, рама или ферма). Определите степень статической неопределимости этого сооружения и выберите для его расчёта симметричную основную систему метода сил. Какой характер носят неизвестные метода сил в полученной основной системе (симметричный, обратносимметричный, несимметричный)? Произведите, при необходимости, группировку несимметричных неизвестных метода сил. Запишите в общем виде систему канонических уравнений относительно принятых неизвестных для расчёта заданного сооружения. Какие побочные коэффициенты этой системы уравнений будут равны нулю и почему? Что произойдёт с системой канонических уравнений после исключения из неё членов с нулевыми побочными коэффициентами?

4. Задано симметричное статически неопределимое сооружение, подверженное симметричному (обратносимметричному) внешнему силовому, температурному или кинематическому воздействию. Выберите симметричную основную систему метода сил, произведите, при необходимости, группировку неизвестных метода сил, запишите в общем виде систему канонических уравнений для расчёта заданного сооружения на симметричное (обратносимметричное) внешнее воздействие. Укажите неизвестные метода сил, равные нулю, при симметричном (обратносимметричном) внешнем воздействии. Объясните, почему при указанном характере внешнего воздействия эти неизвестные метода сил равны нулю?

18.6. Рекомендуемая литература

1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с.

Гл. 6. Метод сил. § 6.8. Возможные упрощения при расчёте статически неопределимых систем методом сил. – С. 142–147.

2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дар­ков, Н.Н. Шапошников. – М.: Высш. школа, 1986. – 607 с.

Гл. 6. Расчёт статически неопределимых систем методом сил. § 6.10. Использование симметрии. § 6.11. Группировка неизвестных. § 6.12. Симметричные и обратносимметричные нагрузки. – С. 238–245. § 6.15. Примеры расчёта рам. – С. 249–263.

3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащени­ков, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.

Гл. XI. Метод сил. § 61. Способы разделения неизвестных в системе канонических уравнений. – С. 335–349.

4. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики. Статика стержневых систем: Учеб. пособие / Г.К. Клейн, Н.Н. Леонтьев. – М.: Высш. школа, 1980. – 384 с.

Гл. IX. Расчёт рам методом сил. § IX.2. Использование симметрии при расчёте рам. – С. 145–159.

5. Анохин Н.Н. Строительная механика в примерах и задачах. Ч. 2. Статически неопределимые системы: Учеб. пособие / Н.Н. Анохин. – М.: Изд-во ассоциации строительных вузов, 2000. – 464 с.

Гл. 5. Расчёт сооружений методом сил. § 5.1. Основная идея метода сил. Выбор рациональной основной системы. Пример 5.2. – С. 12–14. Примеры 5.6–5.9. – С. 15–19. Пример 5.11. – С. 20.

Библиографический список

1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с.

2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дарков, Н.Н. Шапошников. – М.: Высш. школа, 1986, – 607 с.

3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников. – М.: Стройиздат, 1981, – 512 с.

4. Снитко Н.К. Строительная механика: Учеб. для вузов / Н.К. Снитко. – М.: Высш. школа, 1972. – 487 с.

5. Анохин Н.Н. Строительная механика в примерах и задачах. Ч. 1. Статически определимые системы: Учеб. пособие / Н.Н. Ано­хин. – М.: Изд-во ассоциации строительных вузов, 1999. – 334 с.

6. Анохин Н.Н. Строительная механика в примерах и задачах. Ч. 2. Статически неопределимые системы: Учеб. пособие / Н.Н. Ано­хин. – М.: Изд-во ассоциации строительных вузов, 2000. – 464 с.

7. Доценко И.С. Строительная механика: Учеб. пособие / И.С. Доценко. – Киев: Вища школа, 1986. – 294 с.

8. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики. Статика стержневых систем: Учеб. пособие / Г.К. Клейн, Н.Н. Леонтьев и др. – М.: Высш. школа, 1980. – 384 с.

9. Крамаренко А.А. Лекции по строительной механике стержневых систем. Ч. 1. Статически определимые системы: Курс лекций (лекции № 1–7) / А.А. Крамаренко. – Новосибирск: НГАСУ, 2000. – 136 с.

10. Крамаренко А.А. Лекции по строительной механике стержневых систем. Ч. 2. Статически определимые системы: Курс лекций (лекции № 8–12) / А.А. Крамаренко. – Новосибирск: НГАСУ, 2000. – 104 с.

11. Крамаренко А.А. Расчёт статически неопределимых систем методом сил: Метод. указания / А.А. Крамаренко, Л.А. Ши­ро­ких. – Новосибирск: НГАСУ, 1999. – 44 с.

12. Проценко В.М. Расчёт статически неопределимых рам: Методические указания / В.М. Проценко, В.Г. Себешев. – Новосибирск: НГАС, 1993. – 56 с.

13. Крамаренко А.А. Определение перемещений в статически определимых системах. Статически неопределимые системы: Сборник задач / А.А. Крамаренко, Л.А. Ши­ро­ких. – Новосибирск: НГАС, 1996. – 40 с.

14. Себешев В.Г. Инструкция к программе "MEFOR" расчёта статически неопределимых стержневых систем в матричной форме: Учебная программа / В.Г. Себешев. – Новосибирск: НИСИ, 1988. – 14 с.

15. Себешев В.Г. Основные символы и обозначения, используемые в курсе дисциплин кафедры строительной механики / В.Г. Себешев. – Новосибирск: НГАСУ, 1998. – 27 с.

Лекция семнадцатая

Расчёт статически неопределимых систем методом сил на температурное и кинематическое воздействие

17.1. Расчёт стержневых статически неопределимых систем на температурное воздействие

17.2. Пример расчёта статически неопределимой рамы на температурное воздействие в обычной форме

17.3. Пример расчёта статически неопределимой рамы на температурное воздействие в матричной форме

17.4. Расчёт стержневых статически неопределимых систем на кинематическое воздействие

17.5. Пример расчёта статически неопределимой рамы на смещение опорных связей в обычной форме

17.6. Пример расчёта статически неопределимой рамы на смещение опорных связей в матричной форме

17.7. Вопросы для самопроверки

17.8. Рекомендуемая литература