Как интерпретировать значение критерия хи-квадрат Пирсона?

В том случае, если полученное значение критерия χ² больше критического, делаем вывод о наличии статистической взаимосвязи между изучаемым фактором риска и исходом при соответствующем уровне значимости.

Пример расчета критерия хи-квадрат Пирсона

Определим статистическую значимость влияния фактора курения на частоту случаев артериальной гипертонии по рассмотренной выше таблице:

	Артериальная гипертония есть (1)	Артериальной гипертонии нет (0)	Всего
Курящие (1)
Некурящие (0)
Всего

1. Рассчитываем ожидаемые значения для каждой ячейки:

	Артериальная гипертония есть (1)	Артериальной гипертонии нет (0)	Всего
Курящие (1)	(70*72)/150 = 33.6	(70*78)/150 = 36.4
Некурящие (0)	(80*72)/150 = 38.4	(80*78)/150 = 41.6
Всего

2. Находим значение критерия хи-квадрат Пирсона:

χ² = (40-33.6)²/33.6 + (30-36.4)²/36.4 + (32-38.4)²/38.4 + (48-41.6)²/41.6 = 4.396.

3. Число степеней свободы f = (2-1)*(2-1) = 1. Находим по таблице критическое значение критерия хи-квадрат Пирсона, которое при уровне значимости p=0.05 и числе степеней свободы 1 составляет 3.841.

4. Сравниваем полученное значение критерия хи-квадрат с критическим: 4.396 > 3.841, следовательно зависимость частоты случаев артериальной гипертонии от наличия курения - статистически значима. Уровень значимости данной взаимосвязи соответствует p<0.05.

Также критерий хи-квадрат Пирсона вычисляется по формуле

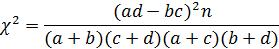(29)

Но для таблицы 2х2 более точные результаты дает критерий с поправкой Йетса

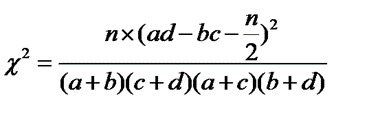
Если 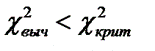то Н(0) принимается,

В случае 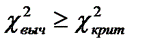принимается Н(1)

Когда число наблюдений невелико и в клетках таблицы встречается частота меньше 5, критерий хи-квадрат неприменим и для проверки гипотез используется точный критерий Фишера. Процедура вычисления этого критерия достаточно трудоемка и в этом случае лучше воспользоваться компьютерными программами статанализа.

По таблице сопряженности можно вычислить меру связи между двумя качественными признаками – ею является коэффициент ассоциации Юла Q (аналог коэффициента корреляции)

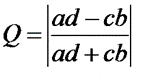
Qлежит в пределах от 0 до 1. Близкий к единице коэффициент свидетельствует о сильной связи между признаками. При равенстве его нулю – связь отсутствует.

Аналогично используется коэффициент фи-квадрат (φ²)

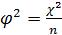(32)

ЗАДАЧА-ЭТАЛОН

В таблице описывается связь между частотой мутации у групп дрозофил с подкормкой и без подкормки

группы	Число культур	всего
Давшие мутации	Не давшие мутации
С подкормкой
Без подкормкой
всего

Анализ таблицы сопряженности

Для анализа таблицы сопряженности выдвигается Н₀- гипотеза .т.е.отсуствие влияния изучаемого признака на результат исследования.Для этого рассчитывается ожидаемая частота ,и строится таблица ожидания.

Таблица ожидания

группы	Чило культур	Всего
Давшие мутации	Не давшие мутации
Фактическая частота	Ожидаемая частота	Фактическая частота	Ожидаемая частота
С подкормкой
Без подкормкой
всего

Метод №1

Определяем частоту ожидания:

1. 3561 – 437

2756 – Х ;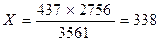

2. 3561 – 3124

2756 – Х ;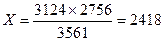

3. 3561 – 437

805 – Х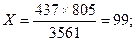

4. 3561 – 3124

805 – Х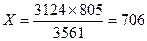

На основании сопоставления таблиц сопряженности и ожидания определяем отклонение фактических частот от ожидаемых

Степень согласия фактических данных с ожидаемым данными определяем с помощью критерий согласия Х^2.

1.Определяем 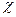² - степень согласия фактических данных с ожидаемыми.

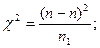
п – фактическая частота

п₁ – ожидаемая частота

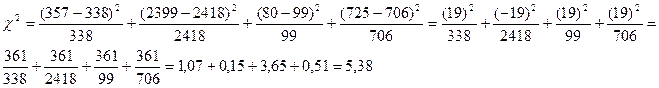
3.Определяем уменьшение неточности с помощью поправки Иейтса.

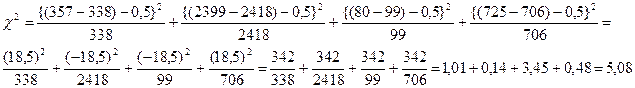
По мере возрастания разницы между фактическими и ожидаемыми данными, Х^{2 -}будет возрастать.

Если число наблюдении в группах мало, при применении Х^2, в случае сопоставления фактических и ожидаемых частот при дискретных распределениях сопряжено с некоторой неточностью.Для уменьшения неточности применяют поправку Йейтса.