Проверка гипотезы о значимости коэффициента корреляции.

О статистической взаимосвязи говорят, что она существует или отсутствует, имеет направление и характеризуется силой.

Если в результате исследования нулевая гипотеза не отвергается, то «взаимосвязи нет» . В случае, когда нулевая гипотеза отклоняется говорят о существовании связи исследуемых случайных величин.

1. Сформулируем гипотезы H₀ и H₁:

H₀: r =0 (корреляции нет),

H₁: r ≠0 (корреляция есть).

2. Зададим уровень значимости α.

3. Статистика критерия

4. t_{α,n-2 .} t-статистика, имеющая распределение Стьюдента с (n-2) степенями свободы.

5. При │t│≥ t_α,n-2 , H₀ отвергается. Это значит, что между параметрами существует значимая корреляция. При │t│< t_α,n-2 , H₀ принимается.

Рисунок 6 - Схематичное изображение различных вариантов зависимостей между переменными X и Y и соответствующие значения коэффициента корреляции Пирсона

В медико-биологических приложениях часто встречаются случаи, когда характеристики взаимосвязанных структур представляются порядковыми переменными. При этом приходится оперировать так называемыми ранговыми коэффициентами корреляции. Кроме того, такой непараметрический подход применяется в случае малых выборок и если изучаемые выборки не распределены по нормальному закону. Так, например, коэффициент корреляции рангов, предложенный К. Спирменом, вычисляется по формуле:

где d_i — разность между рангами сопряженных признаков, п — число парных членов ряда. При полной связи ранги признаков совпадут и разность между ними будет равна 0, соответственно коэффициент корреляции будет равен 1. Если же признаки варьируются независимо, коэффициент корреляции получится равным 0.

Аналогично коэффициент корреляции рангов является оценкой соответствующего генерального параметра, его значимость оценивается с помощью статистики:

где z_а и m связаны соотношениями с уровнем значимости: для α = 5%, z= 1,96 и m = 0,16; для а = 1% z = 2,58, m = 0,69. Нулевую гипотезу отвергают, если полученное значение t_rs превзойдет или окажется равным рассчитанному критическому значению t_rs.

ЗАДАЧА

на применение рангового метода

Задание: методом корреляции рангов установить направление и силу связи между стажем работы в годах и числом травм, если получены следующие данные:

Стаж работы в годах	Число травм
До 1 года
1-2
3-4
5-6
7 и более

Обоснования выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, так как первый ряд признака «стаж работы в годах» имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод - метод квадратов.

РЕШЕНИЕ ЗАДАЧИ

Стаж работы в годах	Число травм	Порядковые номера (ранги)	Разность рангов	Квадрат разности рангов
x	y	d=x-y	d2
До 1 года				-4
1-2				-2
3-4			2,5	0,5	0,25
5-6			2,5	1,5	2,25
7 и более
					Σd2 = 38,5

Произведем расчет коэффициента ранговой корреляции по формуле:

Определим достоверность коэффициента ранговой корреляции.

1-й способ. Определить ошибку (mρxy) коэффициента ранговой корреляции и оценить достоверность его с помощью критерия t:

Полученный критерий t = 5,75 соответствует вероятности безошибочного прогноза (р) больше 99,9%.

ρ_xy = - 0,92 ; mρ_xy = ±0,16 ; t = 5,75 ; р> 99,9 %

2-й способ. По таблице «Стандартных коэффициентов корреляции»: при числе степеней свободы (n — 2) = 5 — 2 = 3 наш расчетный коэффициент корреляции ρxy = –0,92 больше табличного 0,878 и меньше 0,933, что соответствует вероятности безошибочного прогноза больше 95% и меньше 98%. Это позволяет считать полученный коэффициент ранговой корреляции достоверным.

Вывод: с вероятностью безошибочного прогноза (р) больше 95% установлена обратная, сильнаякорреляционная связь между стажем работы и числом травм, т.е. чем меньше стаж работы, тем больше травм.

Обычно, говоря «коэффициент корреляции», подразумевают коэффициент корреляции Пирсона. При этом важно понимать, что такой коэффициент корреляции удовлетворительно характеризует лишь связи, не слишком отклоняющиеся от прямолинейных (линейная зависимость). А значит, если коэффициент корреляции несущественно отличается от нуля, то это не означает отсутствие связи вообще, это говорит только об отсутствии линейной связи между исследуемыми переменными. Первоначально оценить, к какому типу относится данная связь — прямолинейному или криволинейному, можно, построив эмпирическую линию регрессии. Более точно допустимая степень отклонения связи от прямолинейной определяется при помощи критериев криволинейности. Если изучаемая связь является криволинейной, силу такой связи можно оценивать с помощью методов, изложенных в справочниках или книгах.

Пример.Данызначения х и у.

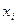	-2
	0,5		1,5

1) найти выборочное уравнение регрессии y от x;

2) построить график регрессии;

3) вычислить коэффициент корреляции;

4) определить силу и характер корреляционной связи.

Решение.n=5

1) рассмотрим несколько способов нахождения выборочного уравнения регрессии y от x;

а) Считая, что зависимость между Х и линейная ( ) вычислим методом наименьших квадратов коэффициент регрессии и свободный член .

. Так как , то регрессия прямая.

.

Тогда уравнение будет иметь вид .

в)(второй способ)

.