Диаграммы на системе полярных координат (радиальные)

Диаграммы, построенные на системе полярных координат, пригодны для изображения сезонных (помесячного, подекадного, понедельного и т. п.) колебаний уровня заболеваемости какой-либо болезнью, размеров смертности, рождаемости и т. п. Для построения таких диаграмм круг де­лят на сектора. Длина радиуса круга соответствует среднему уровню.

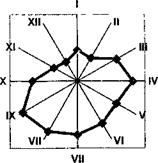•Уровень травматизма

Сезонные колебания (по месяцам года) уровней

транспортного травматизма в текущем году в городе N

На каждом радиусе откладывают и отмечают точкой величину, соот­ветствующую уровню заболеваемости или смертности в данном месяце. Если в этом месяце заболеваемость или смертность была выше среднего­довой, ее отмечают за пределами круга на продолжении радиуса. Располо­жение месяцев года на радиусах круга соответствует движению часовой стрелки (сверху направо вниз и дальше налево вверх). Отмеченные точки соединяются ломаными линиями. Получаются характерные фигуры, на­глядно изображающие сезонность.

Картограммы

Картограммами называются диаграммы, в которых изображено рас­пределение какого-либо явления по территории. Например, если нужно распределить области Российской Федерации по величине коэффициентов рождаемости в 2004 г., то, определив коэффициенты рождаемости для ка­ждой республики, края и области, покрывают на карте РФ эти регионы со­ответствующей раскраской или штриховкой, обозначающей различные размеры коэффициентов.

Картодиаграммы

Картодиаграммы также рисуются на карте (или схеме карты). В каж­дой части территории помещается диаграмма (столбиковая или секторная диаграмма), показывающая динамику или состав изображенного на карто­диаграмме явления в различных частях данной территории.

Каждая диаграмма, к какому бы типу графических изображений она ни относилась, должна иметь четкую и ясную, по возможности краткую надпись, поясняющую изображение. Шкалы на диаграмме должны быть снабжены указателями размеров. Числа рекомендуется надписывать на самой диаграмме или в прилагаемой к ней таблице. Все условные обозначе­ния должны быть объяснены.

3.5 Пятый этап— внедрение результатов исследования в практику и оценка эффективности.

Социально-гигиеническое исследование должно заканчиваться вне­дрением их результатов в практику. В зависимости от целей и задач иссле­дования возможны различные варианты практического использования ре­зультатов работы.

Полученные данные могут быть использованы в докладах и лекциях, по материалам исследования можно подготовить приказ, методические ре­комендации, инструкцию, положение и т. д. На основе результатов иссле­дования может быть проведена реорганизация деятельности медицинского учреждения, результаты работы могут быть оформлены как рационализа­торские предложения, изобретения, открытия, могут быть опубликованы в печати.

Внедрение результатов исследования в практику здравоохранения яв­ляется нередко трудным и многоэтапным процессом.

Контрольные вопросы к разделам 1, 2, 3

1. Определение статистики

2. Медицинская статистика её разделы и задачи

3. Понятие статистической совокупности

4. Дайте понятие единицы наблюдения

5. Генеральная и выборочная совокупность, ее свойства

6. Учетные признаки, их классификация по характеру и роли в совокупности

7. Понятие репрезентативности

8. Способы формирования выборочной совокупности

9. Как рассчитывается необходимая численность выборки
10.Этапы статистического исследования

11.Содержание программы и плана исследования

12.Виды статистического наблюдения (сплошное, несплошное, текущее, единовременное)

13.Виды статистических таблиц. Правила составления, и заполнения ста­тистических таблиц

14.Виды графического изображения

15.Пути внедрения полученных результатов в практику здравоохранения

Занятие 2 - РАЗДЕЛ 4

ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ

Относительные величины весьма распространены и постоянно приме­няются в медицине и здравоохранении. С помощью относительных вели­чин производится сравнение уровней заболеваемости, рождаемости, смертности, сопоставляются показатели деятельности лечебных учрежде­ний.

Однако, в результате сводки материала в разработочных таблицах по­лучаются абсолютные числа, которые характеризуют объем, размер явле­ния. Абсолютные числа не нашли такого широкого применения в медици­не и здравоохранении, как другие статистические величины — относи­тельные и средние.

Абсолютные величины без преобразования их в отно­сительные показатели имеют ограниченное познавательное значение. Ча­ше всего, оперируя абсолютными величинами, нельзя проводить сравнение и сопоставление одной совокупности с другой.

Логическая структура темы «Относительные величины»

Относительные величины

I Область применения

Для характеристики статистических совокупностей

Для сравнения уровня явлений

II Классификация

Экстен­сивные

Интенсив­ные

Соотношения

Нагляд­ности

III Назначение относительных величин

Показывает отношение части к целому

Выражают частоту явлений в непосредственно связанной с ними средами

Характеризуют степени развития явлений в среде, непосредственно с ними не связанной

Дают на­глядные представления о ве­личинах

IV Применение в здравоохранении

Анализ структуры заболе­ваемости

Анализ уровней рождаемо­сти, смерт­ности, заболеваемости

Анализ обеспеченности населения мед. кадра­ми, больнич­ными койками

Анализ показателей здоровья населения

Абсолютные числа для анализа можно использовать в двух случаях:

- это, во-первых, при малых числах наблюдения, в том случае, когда не тре­буется определение закономерности и,

- во-вторых, когда абсолютные циф­ры исчерпали факт, например, при сравнении численности населения по всеобщей переписи населения.

Относительные величины применяют главным образом для характе­ристики распределения признаков в совокупности, а также для сравнения в ходе анализа разных совокупностей.

Различают следующие виды относительных величин: экстенсивные, интенсивные показатели, показатели соотношения и наглядности.

Экстенсивные показатели

Экстенсивные показатели — показатели удельного веса, части в целом, которые характеризуют распределение всего изучаемого явления на со­ставляющие его части.

На основании этого показателя обычно рассматриваются всевозмож­ные структуры: заболеваний, причин смерти, распределение коечного фонда по специальностям, состав операций в больнице и т. п. Выражается экстенсивный показатель обычно в процентах. Способ вычисления: вся со­вокупность принимается за 100%, а искомая часть за х%.

Экстенсивный показатель	=	Абсолютный размер части явления	Х 100%
Абсолютный размер явления в целом

4.2 Интенсивные показатели

Интенсивные показатели — показатели, которые характеризуют распространенность, частоту явления в среде, которая его продуцирует. Обычно в социально-гигиенических исследованиях такой средой является население.

В зависимости от частоты изучаемого явления интенсивные показате­ли рассчитываются на 100, 1000, 10.000, 100.000 населения. Множитель за­висит от распространенности явления в среде, чем реже оно встречается, тем больше множитель. Для вычисления некоторых интенсивных показа­телей множители общеприняты. Так все демографические показатели рас­считываются на 1000 населения, заболеваемость с временной утратой тру­доспособности на 100 работающих, показатели летальности на 100 забо­левших и т. д.

Интенсивный показатель	=	Абсолютный размер явления х 100 (1000, 10000, 100000)
Абсолютный размер среды, продуцирующей данное явление

Показатели соотношения

Показатели соотношения — показатели, которые характеризуют отношение между двумя самостоятельными совокупностями (в этом его сходство с интенсивным показателем), причем независимые совокупности не только связаны друг с другом, но и не продуцируют одна другую (в этом отличие показателя соотношения от интенсивного показателя).

Показатель соотношения	=	Абсолютный размер явления х 100 (1000, 10000, 100000)
Абсолютный размер среды, не продуцирующей данное явление

Показателями соотношения являются показатели обеспеченности на­селения врачами, медсестрами, больничными койками, рассчитанные на 10000 населения. Их широко используют при планировании здравоохранения.

Показатели наглядности

Показатели наглядности — наглядно представляют соотношения показателей, характеризующих один и тот же признак в различных сово­купностях или одно и то же явление в динамике.

В основу вычисления показателя наглядности положен принцип при­нятия одной из величин за 100%, а остальные рассчитываются в процент­ном отношении к ней.

Показатели наглядности можно вычислять на основе интенсивных по­казателей, показателей соотношения и средних величин.

Показатели наглядности указывают, на сколько процентов или во сколь­ко раз произошло увеличение или уменьшение сравниваемых величин.

Показатель наглядности	=	явление х 100
Такое же явление из ряда сравниваемых, принятых за 100%

В применении относительных величин наиболее часто встречаются сле­дующие ошибок:

1 - Интенсивные показатели сравниваются за различные по протяженности периоды наблюдения (помесячные показатели сравниваются с годовыми)

2 - Подмена интенсивного показателя экстенсивным для характеристики уровня, частоты явления, особенно для выявления изменения этого уровня в динамике или по территориям.

3 - При сравнительной оценке экстенсивных показателей в динамике или по территориям надо анализировать всю структуру совокупности, а не сравнивать удельные веса только отдельных его частей

Динамические ряды

Для анализа изменения явления во времени (динамика явления) ис­пользуются динамические ряды.

Динамическим рядом называется совокупность однородных стати­стических величин, показывающих изменения какого-либо явления на протяжении определенного промежутка времен./

Динамический ряд мо­жет состоять из абсолютных или производных величин — относительных чисел и средних.

	Динамические ряды
I. Виды динамических рядов	Простой	Сложный	Моментный	Интервальный

	Динамические ряды
II. Способы выравнивания динамических рядов	Укрупнение интервалов	Вычисление групповой средней	Вычисление скользящей средней

	Динамические ряды
III. Показатели динамического ряда	Абсолютный прирост	Темп прироста	Значение 1% прироста	Темп роста

Числа динамического ряда принято называть уровнями ряда. Разли­чают два основных типа динамических рядов в зависимости от того, из ка­кого рода чисел состоит ряд.

Типы динамических рядов

Ряды могут быть простыми (состоят из абсолютных величин) и сложными(состоят из относительных или средних величин).

Простой динамический ряд может быть двух видов: моментный и ин­тервальный

Моментный, состоит из величин, характеризующих размеры явления на определенное время (например, численность населения РФ на ко­нец соответствующего года).

Интервальным, состоит из чисел, характеризующих величину явле­ния не на какой-либо момент, а за определенный интервал времени (количество родившихся в РФ за год, количество умерших за год и т. п.).