Плоское напряженное состояние

Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю.

На рис.3.8 показано плоское напряженное состояние.

Прямая задача.

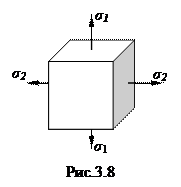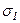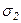Определим напряжения s_x и t_xy, действующие по любой наклонной площадке a по известным главным напряжениям и , т.е. решим так называемую прямую задачу теории напряженного состояния.

Для решения этой задачи воспользуемся принципом независимости действия сил.

Представим плоское напряженное состояние в виде суммы двух независимых линейных напряженных состояний: первое – при действии только напряжений s₁, второе – при действии только напряжений s₂ (рис.3.9)

От каждого из напряжений s₁, s₂ напряжения s_x1, s_x2 и t_xy1,t_xy2 в произвольной площадке равны

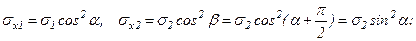
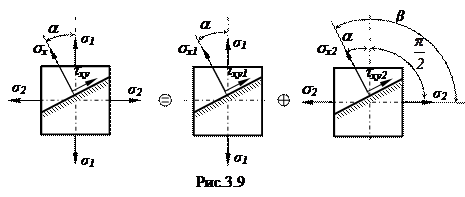
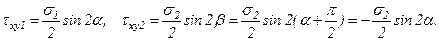
Таким образом, суммируя напряжения, возникшие при каждом линейном напряженном состоянии, получим

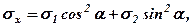
(3.1)

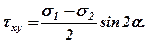
Если рассмотреть площадку с углом наклона 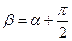, перпендикулярную к площадке a, то можно доказать как и для линейного напряженного состояния, что

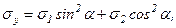
(3.2)

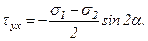
Суммируя нормальные напряжения, действующие по взаимно перпендикулярным произвольным площадкам, получим

.

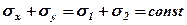Сравнивая величины касательных напряжений, получим

.

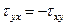Наибольшие касательные напряжения действуют по площадкам, наклоненным к главным под углом a = 45^о

.

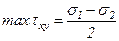Частные случаи плоского напряженного состояния

Всестороннее растяжение

Напряженное состояние, при котором главные напряжения, действующие по граням параллелепипеда равны между собой 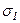= = 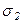s, называется всесторонним растяжением. В этом случае, получим

, ,

, ,

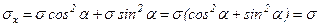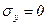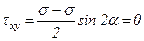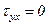то есть, нормальные напряжения в любой произвольной площадке равны между собой 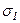= = 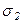= = 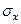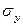s, а касательные напряжения равны нулю: , .

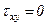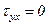Чистый сдвиг

Пусть по граням параллелепипеда действуют главные напряжения 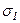=s, 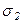= - s , (рис.3.10).

Определим величины нормальных и касательных напряжений, действующих в площадках повернутых под углом 45^о к главным. Из формул (3.1) получим, что

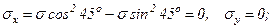
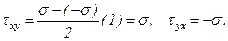
Напряженное состояние, при котором по граням выделенного элемента действуют только касательные напряжения, называется чистым сдвигом, а площадки - площадками чистого сдвига.

Экспериментально установлено, что существует линейная зависимость между углом сдвига g и касательными напряжениями t (рис.3.11), являющейся законом Гука при сдвиге

,

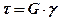где G – модуль сдвига, характеризующий способность материала сопротивляться сдвиговой деформации, т.е. характеризующая жесткость материала при сдвиге.

Величина модуля сдвига связана с модулем упругости при растяжении Е и коэффициентом Пуассона ν соотношением

.

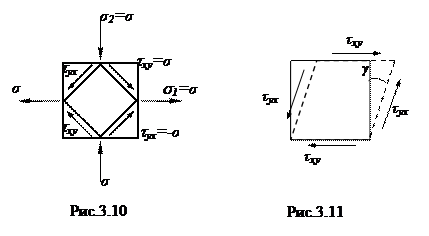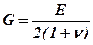Обратная задача

В расчетной практике часто известны не главные напряжения, а напряжения, действующие по некоторым направлениям, например, вдоль продольной линии стержня или балки, по их величинам следует определять главные напряжения, так как именно они играют часто наибольшую роль при оценке прочности элемента конструкции. Таким образом, может быть поставлена обратная задача теории напряженного состояния: по известным напряжениям s_x и s_y, τ_xy, действующим по двум взаимно перпендикулярным площадкам найти величины главных напряжени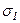й и 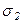и положения главных площадок (угол α₀).

Пусть для определенности положим 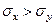. Из формул (3.1) и (3.2), можно получить

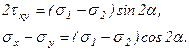(3.3)

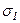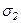Исключив из этих формул и , получим формулу для определения угла наклона главных площадок относительно заданной площадки. Обозначим этот угол 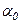. Так как направление отсчета углов 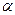для площадки произвольного положения и угла 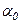противоположны, то в полученной формуле необходимо изменить знак. Положительный угол 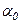будем откладывать от направления внешней нормали к площадке, по которой действуют большие нормальные напряжения 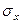против хода часовой стрелки.

.

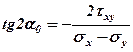Откуда

.

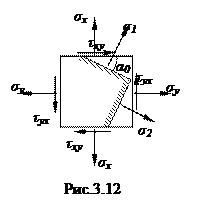
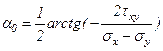Для определения 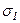и 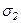возведем каждое из соотношений (3.3) в квадрат и сложим их:

,

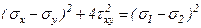тогда

,

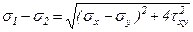а так как 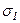+ 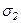= 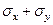, то из двух последних соотношений получим:

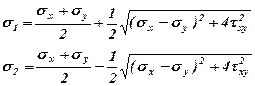(3.4)

Большее главное напряжение 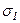действует на площадке с углом наклона a₀, вторая же главная площадка с напряжением 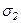ей перпендикулярна и ее нормаль наклонена под углом 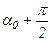к направлению .

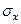Положение главных площадок и направления главных напряжений представлены на рис.3.12.

Главные напряжения обладают свойствами экстремальности, т.е. 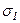наибольшее, а 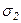наименьшее при любом положении секущей пары взаимно перпендикулярных плоскостей.

1. Понятие о пластическом шарнире. Определение несущей способности балок.

Ответ:

ПЛАСТИЧЕСКИЙ ШАРНИР (шарнир текучести) - сечение балки, полностью находящейся в пластич. состоянии. Понятие "П. ш." приобрело большое значение в связи с исследованием несущей способности стержневых и рамных конструкций. П. ш. возникает в наиб. напряжённых сечениях; напр., если шарнирно опёртая балка (рис.) находится под действием сосредоточенной силы Q, то при увеличении этой силы наибольший изгибающий момент возникает в точке, где образуется П. ш. Появление П. ш. уменьшает степень статич. непреодолимости конструкции и может сделать её статически определимой или даже геометрически изменяемой.

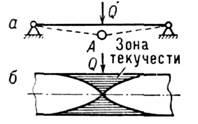
а - образование пластич. шарнира; б - сечение балки в области пластич. шарнира А.

Дальнейшее обобщение понятия П. ш. - цилиндрич. шарнир текучести, образующий прямую или кривую линию на поверхности пластинки или оболочки.