Моменты инерции сечений
Моментами инерции сечения называются геометрические характеристики, определяемые интегралами вида:
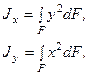(2)
- осевые (экваториальные) моменты инерции относительно осей х и у соответственно;
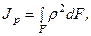(3)
- полярный момент инерции сечения относительно данной точки (полюса), где r - расстояние от площадки dF до полюса,
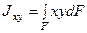(4)
- центробежный момент инерции сечения.
Если полярный момент инерции вычисляется относительно начала системы координат (рис. 4.1), то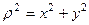 
и
,
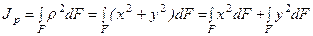следовательно
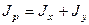, (5)
т.е. сумма осевых моментов инерции сечения относительно любых двух взаимно перпендикулярных осей, проходящих через данную точку равна полярному моменту инерции этого сечения относительно этой точки.
- Особенности деформирования и разрушения материалов в пластичном и хрупком состоянии.
Ответ:
Для пластичного материала условие прочности имеет вид
,
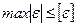где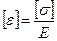 
.
Если, например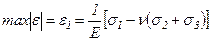 
,
то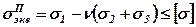 
.
Для хрупкого материала условие прочности имеет вид
,
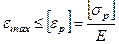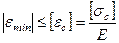
Первая теория дает удовлетворительное совпадение с опытными данными только для хрупких материалов. Вторая практически в настоящее время не применяется.
Третья и четвертая теории прочности дают удовлетворительное совпадение результатов теоретического расчета с опытными данными для пластичных материалов и широко применяются при расчетах на прочность. Для хрупких материалов эти теории не применимы.
Пластичные материалы обладают примерно равными пределами текучести на сжатие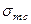 
и на растяжение 
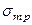равны между собой и поэтому 
.
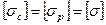Для хрупких материалов, у которых прочность при сжатии выше, чем при растяжении, допускаемые напряжения на растяжение и сжатие, как правило, не равны между собой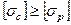 
и, поэтому, необходимо записывать два условия прочности
, 
,
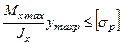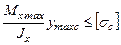где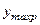 
и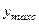 
- расстояния от нейтральной оси до наиболее удаленных растянутого и сжатого волокон.
- Назначение гипотез прочности.
Ответ:
Для расчёта на прочность в условиях сложного напряжённого состояния, строго говоря, необходимо было бы иметь диаграммы испытаний для любой комбинации главных напряжений, характеризующих напряжённое состояние в точке. Однако, понятно, что практически невозможно реализовать экспериментально бесчисленное множество напряжённых состояний. Поэтому необходимо найти такой приём, который позволил бы по экспериментальным данным, полученным при растяжении или сжатии, проводить оценку прочности в условиях любого напряжённого состояния.
Предварительно введём понятие об эквивалентном напряжении. Эквивалентное напряжение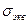 
- это такое напряжение, которое следует создать в растянутом или сжатом образце, чтобы его напряжённое состояние было равноопасно с заданным.
Понятно, что в расчётах на прочность 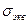через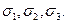 
Для этого существуют несколько гипотез, которые легли в основу технических теорий прочности.
Первая теории прочности – теория максимального нормального напряжения.
Вторая теория прочности – теория максимальной линейной деформации.
Третья теория прочности – теория максимальных касательных напряжений.
Четвёртая теория прочности – энергетическая теория прочности.
Пятая теория прочности – теория прочности Мора.
Билет №5.
- Преобразование геометрических характеристик при повороте координатных осей и их параллельном переносе.
Ответ:
Геометрическими характеристиками являются: площадь поперечного сечения, статические моменты, моменты инерции, моменты сопротивления, радиусы инерции.
Пусть известны моменты инерции произвольных фигур относительно координатных осей х и у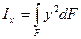 
; 
; 
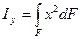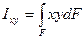
Требуется определить моменты инерции относительно осей х1 и у1, повернутых относительно осей х и у на угол α против часовой стрелки, считая послед. положит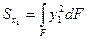 
; 
; 
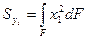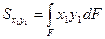
Координаты произвольной элементарной площадки в силовой системе х1у1 могут быть представлены через координаты прежней системы хОу след. образом
; 
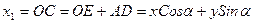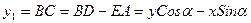
Окончательно находим
; 
; 
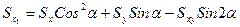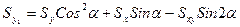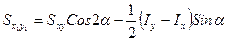
Статические моменты площади
; 
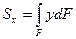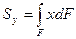
- Основные представления о прочности при напряжениях циклически изменяющихся во времени.
Ответ: