Четвертая теория прочности (энергетическая теория формоизменения)

Очевидно, потенциальная энергия, накопленная в элементарном объеме, определяется суммой работ сил, распределенных по поверхности этого объема. Нормальная сила на перемещении совершает работу. Эта работа имеет величину

где под понимается относительное удлинение вдоль оси , вызванное всеми действующими силами.

Аналогичные выражения работ дают и остальные нормальные составляющие. Касательная сила на перемещении совершает работу

Выражения остальных слагаемых внутренней энергии получаются простой перестановкой индексов. В итоге имеем

Если энергию отнести, как это обычно делается, к единице объема и, кроме того, выразить деформации через напряжения, получим окончательно:

или в главных напряжениях

Для того чтобы найти потенциальную энергию во всем объеме деформированного тела, выражение следует умножить на элементарный объем и проинтегрировать по объему тела:

Выведем выражения для так называемой энергии изменения формы и энергии изменения объема. Эти выражения требуются в дальнейшем при изучении вопросов, связанных с пластическими деформациями и предельными напряженными состояниями. Деление внутренней потенциальной энергии на две указанные составляющие является условным и производится по следующему принципу. Каждое из главных напряжений представляем в виде суммы двух величин

в результате чего напряженное состояние разбивается на два. Первое из них представляет собой всестороннее растяжение, а второе является дополнительным к нему до заданного напряженного состояния (рисунок 2).

Рисунок 2 – К определению энергии изменения объема и энергии формоизменения

Величина подбирается с таким расчетом, чтобы изменение объема в дополнительном напряженном состоянии отсутствовало, т. е.

Складывая выражения (15), получим

При указанном условии система сил первого напряженного состояния не производит работы на перемещениях, вызванных силами второго состояния. Точно так же и силы второго напряженного состояния не производят работы на перемещениях первого. Взаимные работы отсутствуют, и внутренняя энергия разбивается на две части, соответствующие двум напряженным состояниям:

где – энергия изменения объема, а – энергия изменения формы, или энергия формоизменения.

Подставляя в выражение (14) вместо всех главных напряжений величину из (16), получим для первого состояния

Энергию формоизменения определяется путем вычитания из :

или

Если это выражение написать для произвольных осей, то в соответствии с (13)

В частном случае всестороннего равномерного сжатия или растяжения, т. е. при , получаем

При чистом сдвиге, т. е. если

составляющие потенциальной энергии имеют вид

Итак, критерием прочности, согласно четвертой теории, принимается количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом. Согласно этой теории опасное состояние (текучесть) в общем случае напряженного состояния наступает тогда, когда удельная потенциальная энергия формоизменения достигает своего предельного значения. Последнее можно легко определить при простом растяжении в момент текучести.

Условие наступления текучести

Условие прочности

Согласно (18), при простом растяжении в момент текучести ( ) имеем:

Следовательно, условие (20) после подстановки (18), (22) можно записать в виде:

или

Условие прочности будет иметь вид

Приведенное (расчетное) напряжение по четвертой теории

Опыты хорошо подтверждают четвертую теорию для пластичных материалов, одинаково работающих на растяжение и сжатие. Наступление текучести отображается четвертой теорией лучше, чем третьей.

Следует отметить, что выражение (18) с точностью до постоянного множителя совпадает с выражением для касательного напряжения на октаэдрической площадке, равнонаклоненной к трем главным направлениям. Поэтому расчетные уравнения четвертой теории прочности можно получить, исходя из критерия постоянства октаэдрических касательных напряжений:

Такая трактовка освобождает рассматриваемую теорию прочности от ограничений, связанных с областью применимости закона Гука, и дает возможность установить не только условия начала пластических деформаций, но и разрушения.

3 Теория Мора

Эта теория прочности, предложенная О. Мором в начале XX века, исходит из предположения, что прочность материалов в общем случае напряженного состояния зависит, главным образом, от величины и знака наибольшего и наименьшего главных напряжений. Среднее по величине главное напряжение, как указывалось выше, лишь незначительно влияет на прочность. Опыты с медными, никелевыми и чугунными трубками показывают, что погрешность, связанная с тем, что не учитывается , не превышает 12-15%. Учитывая это предположение, мы можем любое напряженное состояние изобразить одним кругом Мора, построенным на главных напряжениях и .

Если при данных и нарушается прочность материала, то круг, построенный на этих напряжениях, называется предельным. Меняя предельное напряженное состояние, мы получим для данного материала семейство предельных окружностей (рисунок 3). Опыты показывают, что по мере перехода из области растяжения в область сжатия прочное сопротивление увеличивается. Это соответствует увеличению диаметров предельных окружностей по мере движения влево.

Рисунок 3 – Семейство предельных кругов напряженного состояния для определения запаса прочности по теории Мора

Огибающая семейства предельных кругов ограничивает область прочности (рисунок 3). Точка соответствует всестороннему равномерному растяжению. Так как при равномерном всестороннем сжатии материал способен, не разрушаясь, выдержать очень большие напряжения, то огибающая слева остается незамкнутой. При наличии предельной огибающей расчет прочности производится весьма просто. По найденным значениям главных напряжений и строят круг. Прочность будет обеспечена, если он целиком лежит внутри огибающей. Огибающую определяют путем построения нескольких опытных кругов при различных комбинациях главных напряжений.

В практических приложениях небольшой участок огибающей строят на основании двух опытов – на растяжение и сжатие, причем предельную кривую заменяют прямыми линиями, касательными к окружностям (рисунок 3).

Допускаемое напряженное состояние можно получить, уменьшив масштаб чертежа в раз ( – коэффициент запаса). На рисунке 4 показано допускаемое напряженное состояние для небольшого участка огибающей.

Легко получить условие прочности для промежуточного напряженного состояния , центр круга которого 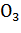располагается между точками (рисунок 4). Проведем прямые соединяющие центры и точки касания окружностей с огибающими линиями, а также прямую , параллельную . Из подобия треугольников получим следующие зависимости:

Рисунок 4 – К определению условия прочности по теории Мора

Заменив отрезки линий значениями соответствующих напряжений, будем иметь:

После преобразования, вводя знак неравенства, получаем условие прочности:

При одинаковом сопротивлении материала растяжению и сжатию огибающая на указанном участке проходит параллельно оси абсцисс и расчетная формула (27) совпадает с (10), полученной по третьей теории прочности.

Достоинства теории Мора бесспорны, так как она основана на опытных данных. Основные недостатки этой теории следующие:

- построение предельной огибающей для каждого материала может быть произведено в результате постановки ряда сложных опытов с плоскими и объемными напряженными состояниями, что, собственно, и ограничивает ее применение;

- теория, как уже отмечалось, не учитывает влияния на прочность промежуточного главного напряжения .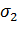

О применимости той или иной теории прочности для практических расчетов можно сказать следующее. Разрушение материалов происходит путем отрыва за счет растягивающих напряжений или удлинений и путем среза за счет наибольших касательных напряжений. При этом разрушение путем отрыва может происходить при весьма малых остаточных деформациях или вовсе без них (хрупкое разрушение). Разрушение путем среза имеет место лишь после некоторой остаточной деформации (вязкое разрушение). Отсюда ясно, что вторую и первую теории прочности, отражающие разрушение путем отрыва, можно применять лишь для материалов, находящихся в хрупком состоянии. Третью и четвертую теории прочности, хорошо отражающие наступление текучести и разрушение путем среза, надлежит применять для материалов, находящихся в пластическом состоянии.

Теория прочности Мора позволяет установить сопротивление разрушению материалов, обладающих разными сопротивлениями растяжению и сжатию. При этом ветвь (рисунок 3) характеризует разрушение от среза, ветвь – от отрыва. Так как первая и вторая теории прочности страдают существенными недостатками, то в настоящее время утверждается мнение о нежелательности их применения. Таким образом, для практических расчетов следует рекомендовать четвертую (или третью) теорию прочности для материалов, одинаково сопротивляющихся растяжению или сжатию, и теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию, т.е. хрупких материалов (для этих материалов в настоящее время пока еще применяется и вторая теория прочности).

Следует подчеркнуть, что хрупкое или пластическое состояние материала определяется не только его характером, но и видом напряженного состояния, температурой и скоростью нагружения. Рядом опытов было показано, что пластичные материалы при определенных условиях нагружения и температуре ведут себя как хрупкие, в то же время хрупкие материалы при определенных напряженных состояниях ведут себя как пластичные. Так, например, при напряженных состояниях, близких к всестороннему равномерному растяжению, пластичные материалы разрушаются как хрупкие. Такие напряженные состояния принято называть «жесткими». Весьма «мягкими» являются напряженные состояния, близкие к всестороннему сжатию. В этих случаях хрупкие материалы могут вести себя как пластичные. При всестороннем равномерном сжатии материалы могут выдержать, не разрушаясь, очень большие давления. Следует отметить, что перечисленные теории прочности не применимы для расчета прочности в случае всестороннего сжатия .

4 Диаграммы механического состояния

Диаграмма механического состояния строится на основании следующих положений:

1. Материалы могут разрушаться от растягивающих напряжений или удлинений путем отрыва и путем среза – от касательных напряжений. Соответственно этому различают две характеристики прочности – сопротивление отрыву которое представляет собой величину нормальных напряжений на поверхности разрушения в первом случае, и сопротивление срезу , представляющее собой величину касательных напряжений во втором случае.

2. Обе характеристики прочности 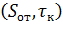не зависят от типа напряженного состояния.

3. Кривая деформации материала в координатах также не зависит от напряженного состояния.

Нарушение прочности путем отрыва описывается теорией наибольших относительных удлинений:

а нарушение прочности второго вида – теорией наибольших касательных напряжений:

Диаграмма механического состояния состоит из двух диаграмм (рисунок 5) – собственно диаграммы механического состояния (слева) и кривой деформации . При построении диаграммы по оси ординат откладывают наибольшее касательное напряжение по оси абсцисс – наибольшее приведенное растягивающее напряжение по второй теории прочности . На диаграмму наносят предельные линии, соответствующие пределу текучести при сдвиге и сопротивлению срезу . Отклонение линии сопротивления отрыву вправо выше предела текучести соответствует возрастанию сопротивления отрыву с появлением остаточных деформаций.

Рисунок 5 – Диаграммы механического состояния

Для характеристики типа напряженного состояния вводится коэффициент «мягкости», представляющий собой отношение наибольшего касательного напряжения в точке к наибольшему приведенному растягивающему напряжению:

Различные напряженные состояния, таким образом, при возрастании нагрузки изображаются на диаграмме лучами, тангенсы углов которых равны 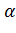. Например, при всестороннем растяжении и луч совпадает с осью абсцисс. При простом растяжении имеем:

при простом сжатии :

Принимая , находим . Рассматривая лучи, отве­чающие различным типам напряженного состояния материала, можем приближенно установить вид разрушения и выбрать, следовательно, подходящую теорию прочности. Например, луч 1 на диаграмме пересекает раньше всего линию сопротивления отрыву. Следовательно, материал разрушится путем отрыва без предшествующей пластической деформации. Луч 2 пересекает сначала линию текучести, а затем линию сопротивления отрыву. Следовательно, при данном напряженном состоянии разрушение произойдет путем отрыва, но с предшествующей пластической деформацией. Для напряженного состояния, соответствующего лучу 3, после пластической деформации разрушение произойдет путем среза. В тех случаях, когда лучи, изображающие то или иное сложное напряженное состояние, пересекают прежде всего линию сопротивления отрыву, расчет прочности следует производить по теории Мора, второй или первой теориям прочности. Если же вначале пересекается линия предела текучести, то расчет прочности надлежит производить по третьей или четвертой теориям прочности.

Таким образом, диаграммы механического состояния с известным приближением отражают зависимость формы разрушения от вида напряженного состояния. Приближённость построения заключается в том, что предел текучести и сопротивление разрушению не являются постоянными. Лучи, изображающие напряженные состояния, являются прямыми лишь до достижения предела текучести.