Теория метода исследования
Прежде чем перейти к описанию конкретных методов измерения времени жизни, приведем некоторые соображения, служащие основой такого рода измерений. Пусть имеется полупроводник в виде бруска, длина которого велика по сравнению с поперечными размерами («нитевидидный» образец, внутри которого возникает 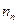 дополнительных носителей в одном кубическом сантиметре в одну секунду) например, вследствие освещения области 1, Рис.2.
дополнительных носителей в одном кубическом сантиметре в одну секунду) например, вследствие освещения области 1, Рис.2.
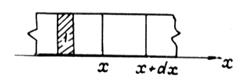
Рис. 2. Одномерная модель нитевидного образца: 1 - освещенная область
Рассмотрим слой полупроводника, ограниченный плоскостями 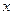 и
и 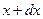 . Через сечение
. Через сечение 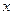 в рассматриваемый слой через
в рассматриваемый слой через 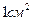 в 1 секунду входит вследствие диффузии число носителей:
в 1 секунду входит вследствие диффузии число носителей: 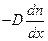 (D-коэффициент диффузии), а за это же время выходит через сечение
(D-коэффициент диффузии), а за это же время выходит через сечение 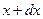 :
:
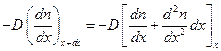 .
.
Следовательно, увеличение числа носителей слоя вследствие диффузии примет следующий вид:
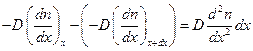 .
.
Если в полупроводнике имеется электрическое поле 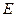 , то носители участвуют еще в переносном «дрейфовом» движении. Число носителей, входящих вследствие дрейфа через сечение
, то носители участвуют еще в переносном «дрейфовом» движении. Число носителей, входящих вследствие дрейфа через сечение 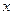 через
через 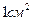 в секунду равно:
в секунду равно:
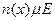 ,
,
где 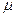 - подвижность, а число носителей, выходящих через
- подвижность, а число носителей, выходящих через 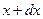 , выражается формулой
, выражается формулой
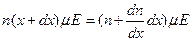 .
.
Увеличение числа носителей в слое за одну секунду равно:
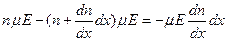 .
.
В стационарном состоянии полное число носителей, вошедших в слой, должно равняться числу носителей, исчезающих вследствие рекомбинации (также за одну 1 с.), (см. формулу (1))
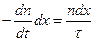 .
.
Поэтому уравнение баланса дополнительных носителей одного знака (например, электронов в дырочном материале) будет иметь вид:
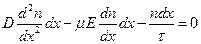
или
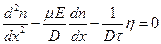 . (3)
. (3)
Заметим, что уравнение (3) справедливо только для малых значений концентрации неосновных носителей 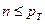 (по сравнению с концентрацией основных носителей).
(по сравнению с концентрацией основных носителей).
Действительно, для стационарного случая необходимым является выполнение уравнения непрерывности
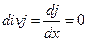 ,
,
где плотность тока 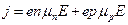 составляется из потока дырок и электронов. Следовательно, в общем случае нужно было бы решать уравнение баланса носителей обоих знаков. Однако можно приближенно считать, что уравнение непрерывности соблюдается и в нашем случае.
составляется из потока дырок и электронов. Следовательно, в общем случае нужно было бы решать уравнение баланса носителей обоих знаков. Однако можно приближенно считать, что уравнение непрерывности соблюдается и в нашем случае.
Используем соотношение Эйнштейна
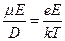 , (4)
, (4)
где 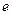 - заряд электрона,
- заряд электрона, 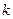 - постоянная Больцмана и введем обозначения:
- постоянная Больцмана и введем обозначения:
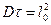 , (5)
, (5)
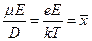 . (6)
. (6)
Тогда уравнение (3) принимает следующий вид:
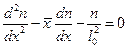 . (7)
. (7)
общее решение этого уравнения имеет вид:
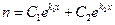 , (8)
, (8)
где 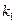 и
и 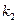 удовлетворяют характеристическому уравнению
удовлетворяют характеристическому уравнению
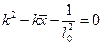 .
.
Откуда
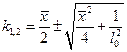 .
.
Так как физический смысл имеет только затухающие решения, то 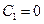 , ибо
, ибо 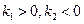 , и мы имеем:
, и мы имеем:
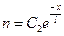 ,
,
где
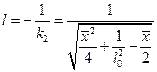 . (9)
. (9)
Так как при 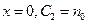 , то окончательно
, то окончательно
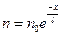 . (10)
. (10)
Следовательно, концентрация неравновесных носителей заряда убывает по показательному закону с увеличением расстояния. Величина 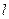 ‚ определяемая формулой (9), есть длина запаздывания носителей, т.е. расстояние, на котором их концентрация уменьшается в e=2.718… раз.
‚ определяемая формулой (9), есть длина запаздывания носителей, т.е. расстояние, на котором их концентрация уменьшается в e=2.718… раз.
Исследуем решение для двух предельных случаев.
1. 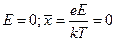 .
.
В этом случае 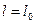 и решение (10) принимает вид:
и решение (10) принимает вид:
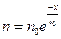 . (11)
. (11)
Здесь 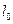 есть «диффузионная» длина носителей заряда, т.е. такое расстояние, на котором концентрация носителей, распространяющихся только вследствие диффузии (в отсутствие поля), уменьшается в е раз в результате рекомбинации.
есть «диффузионная» длина носителей заряда, т.е. такое расстояние, на котором концентрация носителей, распространяющихся только вследствие диффузии (в отсутствие поля), уменьшается в е раз в результате рекомбинации.
2. 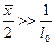 . Тогда имеем:
. Тогда имеем:
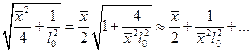
Подставляя это выражение в (9), имеем
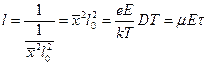 . (12)
. (12)
Подставляя это выражение в формулу (10) и учитывая ещё, что 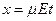 , где
, где 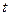 - время движения носителей, находим
- время движения носителей, находим 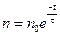 , т.е. опять формулу (2).
, т.е. опять формулу (2).
Полученные результаты лежат в основе экспериментального определения времени жизни 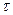 . Видно, что для этого можно либо исследовать уменьшение концентрации неравновесных носителей
. Видно, что для этого можно либо исследовать уменьшение концентрации неравновесных носителей 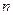 с течением времени и найти
с течением времени и найти 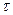 по формуле (2), либо исследовать зависимость
по формуле (2), либо исследовать зависимость 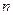 от расстояния вдоль образца. В последнем случае мы определяем диффузионную длину
от расстояния вдоль образца. В последнем случае мы определяем диффузионную длину 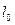 по значению которой, зная коэффициент диффузии D, можно найти
по значению которой, зная коэффициент диффузии D, можно найти 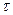 по формуле (5).
по формуле (5).
Величину D можно определить из данных о подвижности, пользуясь соотношением Эйнштейна (4).
