Дифракция на двумерной структуре

МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РЕСПУБЛИКИ БЕЛАРУСЬ

ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Имени П.О.Cухого.

Кафедра”Физика”

Лабораторная работа №4

Определение периодов двухмерной структуры.

Выполнил студент гр.ПЭ-23:

Миньков А.А.

Принял преподаватель:

Петрашенко П.Д.

Гомель 2002

Лабораторная работа №4

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ. ОПРЕДЕЛЕНИЕ ПЕРИОДОВ ДВУХМЕРНОЙ СТРУКТУРЫ.

Цель работы: изучение дифракции света на одномерной и двухмерной структурах

Приборы и принадлежности: ОКГ, дифракционная решётка, металлическая сетка, экран.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

При подготовке к лабораторной работе необходимо теоретические сведения к работе №3 "Изучение дифракции от щели".

Дифракционной решёткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей. Расстояние d между серединами соседних щелей называется периодом решетки. Расположим параллельно решётке RR. собирающую линзу Л Л , в фокальной плоскости которой поставим экран ЭЭ. Выясним характер дифракционной картины, получающейся на экране при падении на решётку плоской световой волны ( для простоты будем считать, что волна падает на решётку нормально). Каждая из щелей даст на экране картину, типичную для дифракции от одной щели. Картины от всех щелей придутся на одно и то же место экрана ( т.к. независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку Р от различных щелей, были некогерентными, результирующая картина от N щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в N раз. Однако колебания от различных щелей являются когерентными, поэтому результирующая интенсивность будет отлична от NJφ ( Jφ - интенсивность, создаваемая одной щелью в направлении φ ).

Результирующее колебание в точке Р, положение которой определяется углом (φ, представляет собой сумму N колебаний с одинаковой амплитудой Аφ , сдвинутых друг относительна друга по фазе на одну и ту же величину δ.

Дифракционная картина от решетки является результатом дифракции волн на каждой щели (Jφ) и интерференции волн от различных щелей

Разность хода от соседних щелей равна :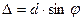

Следовательно, разность фаз равна: 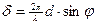(2)

Подставим в формулу (I) выражение для Jφ и выражение (2) для δ, получим:

dsinφ = 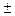mλ

Для направлений, определяемых этим условием, колебания от отдельных щелей взаимно усиливают друг друга, вследствие чего амплитуда колебаний в соответствующих точках экрана равна Amax=NAφ.

Условие (5) определяет положения максимумов интенсивности, называемых главными. Число m называется порядком главного максимума. Максимум нулевого порядка только один. максимумов 1-го, 2-го, и т.д. порядков имеется по два.

Возведя равенство (6) в квадрат, получим, что интенсивность главных максимумов Jmax в N2 раз больше интенсивности

Jφ , создаваемой в направлении 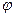одной щелью

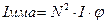
Следовательно, при дифракции света на решетке из N правильно расположенных щелей, интенсивность растёт прямопропорционально квадрату числа щелей. Это есть следствие перераспределения полной , прошедшей через все щели световой энергии вследствие интерференции дифрагировавших пучков.

Кроме минимумов, определяемых условием (4), в .промежутках. между соседними главными максимумами имеется по (N-1) добавочному минимуму. Эти минимумы возникают в тех направлениях , для которых колебания от отдельных щелей взаимно погашают друг друга.

Направление добавочных минимумов определяется условием

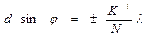(8)

В формуле (8) К` принимает все целочисленные значения кроме 0, N, 2N… , т.е. кроме тех, при которых условие (8) переходит в условие (5).

Положение главных максимумов зависит от длины волны λ. Поэтому при пропускании через решетку белого цвета все максимумы, кроме центрального разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный – наружу. Т.о., дифракционная решетка представляет собой спектральный прибор.

Дифракция на двумерной структуре.

В работе исследуется дифракция луча He-Ne. лазера на двумерных структурах, в качестве которых используются сетки с прямоугольными равными по размерам ячейками. При рассмотрении одномерной задачи дифракции плоской волны на правильной структуре из m щелей учитывается изменение распределения интенсивности дифрагированного света лишь вдоль направления, перпендикулярного к образующим щелей. Ери перемещении же приемника вдоль образую-щих щелей эффектов дифракции не наблюдается . Представляет инте­рес рассмотреть дифракцию света в более сложных структурах. Рассмотрим двумерную систему, а именно две дифракционные решётки с периодами d1 и d2. Наложим их одна на другую так, чтобы щели первой решётки были перпендикулярны к щелям второй. Пусть ось X перпендикулярна к щелям первой решётки, а ось У - к щелям второй. При описании такой более сложной системы будем пользоваться не углами дифракции φ1 , а дополнительными к ним углами α , β ,γ. Очевидно, что sinφ1=cosα.

Тогда известное условие возникновения главных максимумов для первой решётки запишется в виде

Пусть нормально на такую систему двух дифракционных решеток падает плоская волна. Если обозначим через α0, β0, γ0, углы

между нормалью к плоской волне и осями x,y,z то в нашем случае α0=β0=π/2; γ0=0. Применяя теорию одномерной решетки, найдём, что положения главных максимумов в направлении оси должны удовлетворять условию:

Таким образом главные максимумы дифрагированного на двумерной структуре света возможны лишь в направлениях, удовлетворяющих

одновременно двум написанным выше условиям. Если в каждой решетке, образующих двумерную структуру, число щелей N1 и N2 достаточно велико, то максимумы будут очень острыми и практически вся световая энергия пойдёт только по этим "разрешетным" направлениям. На экране, расположенном в любом месте за системой решеток, получится дифракционная картина, представляющая собой четкие, симметрично расположенные световые пятна

ПРАКТИЧЕСКАЯ ЧАСТЬ

Ход работы

а) Определение длины световой волны с помощью дифракционной решетки

1. Установим элементы установки согласно рисунку. Добьёмся появления на экране чёткой дифракционной картины. Расстояние а должно лежать в пределах 0,4-0,6 м.
2. измерим с помощью миллиметровой линейки расстояние между решеткой и экраном (а) и расстояние Х1l , X2p, X1p, X2l. Результаты измерений занесем в таблицу I. m-порядок максимума.

№	m	a, мм	X1l, мм	X1р, мм	X2l, мм	X2p, мм	Хi, мм	λi нм	λсp нм	Δλ нм
					-	-	25,2	0,00063	0,000625	0,000005
			-	-				0,0006625	0,0006625
					-	-	34,5	0,00069	0,00068	0,00001
			-	-				0,00068	0.00068

1. Изменим расстояние а и выполним требования пункта 2. Результаты измерений занесём в таблицу I

(строки 3,4).

1. Вычислим среднее значение Хi и занесём в таблицу I

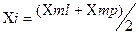
1. Значение длины волны может быть определено из условия максимума:

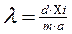
где d=0,01 мм- период решётки

6. Вычислим 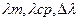. Результат в нанометрах занесём в таблицу.

б) Определение периодов двухмерной структуры

1. Заменим дифракционную решетку на металлическую сетку (С). расстояние а должно лежать в пределах 0,6-1 м.

2. Измерим с помощью миллиметровой линейки расстояние между сеткой и экраном (а) и расстояние X1, X2, Y1, Y2. Результаты измерений занесём в таблицу 2.

№	M	a, мм	Хм, мм	Yм, мм	d1, мм	d2, мм
					0,015	0,0318
					0,00816	0,01813

3. Значение d1 и d2 могут быть определены из условий максимума:

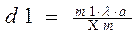
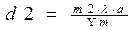
Вывод: Изучили дифракцию света на одномерной и двумерной структурах.