III. Работа над новым материалом. Прием умножения для случаев вида 23 · 4 основан на применении правила умножения суммы
Прием умножения для случаев вида 23 · 4 основан на применении правила умножения суммы на число. Для сознательного восприятия этого приема достаточно знать это правило и уметь представить число в виде суммы разрядных слагаемых. Поэтому в качестве подготовки к рассмотрению нового материала и следует повторить эти вопросы, включив соответствующие задания в устные упражнения:
1) представьте числа 45, 68, 72, 26 в виде суммы разрядных слагаемых:
45 = 40 + 5 72 = 70 + 2
68 = 60 + 8 26 = 20 + 6
2) вычислите результаты разными способами:
(4 + 2) · 5 = 6 · 5 = 30
(6 + 3) · 9 = 9 · 9 = 81
(4 + 2) · 5 = 4 · 5 + 2 · 5 = 20 + 10 = 30
(6 + 3) · 9 = 6 · 9 + 3 · 9 =54 + 27 = 81
Объяснение нового приема можно начать сразу с рассмотрения в учебнике развернутой записи решения примера 23 · 4 и данной к нему иллюстрации.
Учитель. Как можно вычислить произведение 23 · 4 с помощью сложения?
Попросить объяснить иллюстрацию.
Учащиеся. 23 нужно повторить слагаемым 4 раза. На рисунке показано это, а число 23 изображено, как 20 и 3.
Учитель. Посмотрите на записи и объясните, что сделали сначала.
Учащиеся. Число 23 представили в виде суммы разрядных слагаемых 20 и 3.
Учитель. Теперь надо умножить эту сумму на 4. Объясните, как это сделали по записи и по рисунку.
Учащиеся. Сначала умножили первое слагаемое 20 на 4, потом – второе слагаемое 3 также умножили на 4 и полученные результаты сложили. На рисунке видно, что можно найти сначала, сколько будет 20 · 4, а потом 3 · 4.
После того как будет объяснено решение примера 23 · 4, можно предложить детям самостоятельно объяснить, как найти произведение 4 · 23 и какое свойство умножения при этом использовать.
Учащиеся должны сами выделить 3 основных этапа, из которых складывается решение примера вида 23 · 4: 1) заменить первый множитель суммой разрядных слагаемых, 2) прочитать полученное выражение (20 + 3) · 4 и 3) вычислить произведение удобным способом: умножить на число каждое слагаемое в отдельности и полученные произведения сложить.
Для первичного закрепления на доске и в тетрадях с подробной записью каждого шага в рассуждении решить примеры № 1.
36 · 2 = (30 + 6) · 2 = 30 · 2 + 6 · 2 = 60 + 12 = 72
5 · 16 = 5 · (10 + 6) = 5 · 10 + 5 · 6 = 50 + 30 = 80
24 · 4 = (20 + 4) · 4 = 20 · 4 + 4 · 4 = 80 + 16 = 96
13 · = (10 + 3) · 3 = 10 · 3 + 3 · 3 = 30 + 9 = 39
Ф и з к у л ь т м и н у т к а
IV. Работа над пройденным материалом.
1. Для закрепления навыков табличного умножения и деления можно предложить детям записать все числа от 1 до 80, которые делятся на 8 (I вариант) и числа от 1 до 70, которые делятся на 7 (II вариант), составить по 3 примера на умножение числа 6 (9) на однозначное число.
I вариант II вариант
8, 16, 24, 32, 40, 48, 56, 64, 72 7, 14, 21, 28, 35, 42, 49, 56, 63
6 · 5 = 30 9 · 3 = 27
6 · 8 = 48 9 · 5 = 45
6 · 9 = 54 9 · 9 = 81
2. Решение задач. Задачу № 2 следует разобрать под руководством учителя. По ходу повторения и первичного анализа ее текста учитель под диктовку детей записывает ее кратко в таблице.
| Масса 1 п. | Кол-во п. | Масса всех посылок |
| К. 8 кг | Одинаковое | 32 кг |
| Ф. 6 кг | ? |
После того как по таблице будет повторено, что дано в задаче и что нужно узнать, учитель должен обратить внимание детей на то, что известно о посылках с книгами, спросить, что можно узнать по этим данным.
Учащиеся. Зная, что масса всех посылок равна 32 кг, а масса каждой посылки 8 кг, можно узнать, сколько было посылок с книгами.
Затем надо выяснить, поможет ли это ответить на вопрос задачи.
Учащиеся. Поможет, потому что с фруктами было столько же посылок, сколько с книгами.
Учитель. Зная, сколько было посылок с фруктами и массу каждой посылки, можно будет узнать, какова масса всех посылок с фруктами.
Далее вызванный ученик кратко формулирует план решения.
П л а н р е ш е н и я:
Сначала узнаем количество посылок с книгами.
Потом узнаем массу всех посылок с фруктами.
Записать решение дети должны самостоятельно.
1) 32 : 8 = 4 (п.) – с книгами
2) 6 · 4 = 24 (кг)
О т в е т: 24 кг весят посылки с фруктами.
3. Для самостоятельной работы предложить решить задания № 3 и № 6.
V. Итоги урока.
Учитель. Ребята, что нового узнали на уроке?
Дети. На уроке мы познакомились с новым приёмом умножения.
Учитель. Что повторяли сегодня на уроке?
Дети. Повторяли решение задач, перевод единиц длины, табличные случаи умножения и деления.
Домашнее задание:с. 7, № 6.
У р о к и 6 и 7. ЗАКРЕПЛЕНИЕ ПРОЙДЕННОГО (с. 8–9)
Цели:закрепить умение умножать двузначные числа на однозначное и решать задачи, умение чертить отрезки, находить периметр четырёхугольника, решать уравнения.
Ход уроков
I. Организационный момент.
II.Уроки строятся по усмотрению учителя. Все задания, представленные на страницах учебника, могут быть использованы для организации самостоятельной работы детей с последующей проверкой в классе. В устные упражнения полезно включить примеры на табличное умножение и деление, а также на повторение соотношений между единицами длины.
III. Итоги уроков.
Учитель.Ребята, что повторяли сегодня на уроке?
Учащиеся.Повторяли умножение двузначного числа на однозначное, составляли по таблицам задачи и решали их, чертили отрезки заданнойдлины, находили периметр четырёхугольника, повторяли случаи умножения и деления с 0 и 1, решали уравнения.
Домашнее задание:с. 8, № 8; с. 9, № 6.
У р о к 8. НАХОЖДЕНИЕ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ С БУКВАМИ
ПРИ ЗАДАННЫХ ЧИСЛОВЫХ ЗНАЧЕНИЯХ ВХОДЯЩИХ В НИХ
БУКВ(с. 10)
Цели: познакомить учащихся с нахождением значения выражений с двумя переменными; отрабатывать навык решения задач и примеров.
Ход урока
I. Организационный момент.
II. Устный счёт.
1. Устно следует решать примеры на изученные случаи умножения и деления двузначных чисел:
40 · 2 60 : 30 80 : 4
30 · 2 80 : 40 60 : 3
10 · 5 90 : 30 100 : 5
Примеры лучше записать на доске.
2. Для устной работы также можно предложить «Лабиринт» (на полях учебника) и задание № 3.
Задание «Лабиринт»
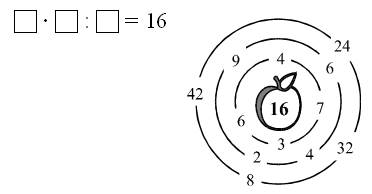
З а д а н и е № 3.
Ширина тротуара 3 м, а ширина проезжей части в 9 раз больше. Объясните, что означают выражения: 3 · 9; 3 · 2; 3 · 9 + 3 · 2.
