Напряжения при растяжении и сжатии

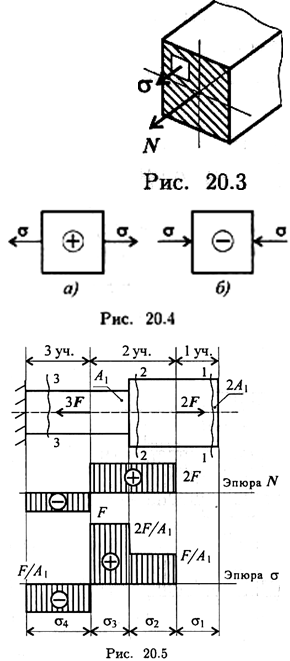При растяжении и сжатии в сечении действует только нормаль­ное напряжение.

Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.

Таким образом, направление и знак напряжения в сечении сов­падают с направлением и знаком силы в сечении (рис. 20.3).

Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по форму­ле

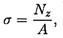
где N_z — продольная сила в сечении; А — площадь поперечного сечения.

Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.

Нормальные напряжения действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.4б).

Размерность (единица измерения) напряжений — Н/м² (Па), од­нако это слишком малая единица, и практически напряжения рас­считывают в Н/мм² (МПа):

1 МПа = 10⁶ Па =1 Н/мм².

При определении напряже­ний брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.

Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.

Строится и оформляется такая эпюра так же, как и эпюра про­дольных сил.

Рассмотрим брус, нагру­женный внешними силами вдоль оси (рис. 20.5).

Обнаруживаем три уча­стка нагружения и определяем величины продольных сил.

Участок 1: N₁ = 0. Внут­ренние продольные силы равны нулю.

Участок 2: N₂ = 2F. Продольная сила на участке положительна.

Участок 3: N₃ = 2F – 3F = - F. Продольная сила на участке отрицательна.

Брус – ступенчатый.

С учетом изменений величин площади поперечного сечения участков напряжений больше.

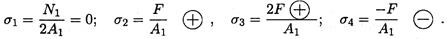
Строим эпюры продольных сил и нормальных напряжений.

Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.

Примеры решения задач

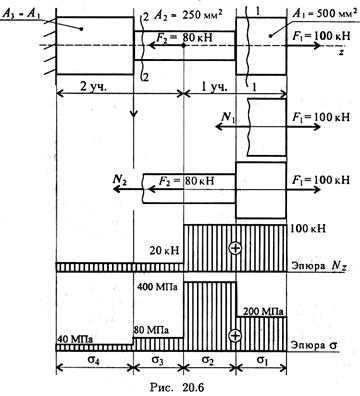Пример 1. Ступенчатый брус нагружен вдоль оси двумя силами. Брус за­щемлен с левой стороны (рис. 20.6). Пренебрегая весом бруса, по­строить эпюры продольных сил и нормальных напряжений.

Решение

— Определяем участки нагружения, их два.

— Определяем продольную силу в сечениях 1 и 2.

— Строим эпюру.

— Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном мас­штабе.

1. Определяем продольные силы.

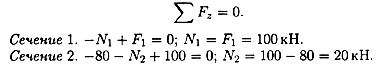
В обоих сечениях продольные силы положительны.

2. Определяем нормальные напряжения

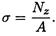
Сопоставляя участки нагружения с границами изменения пло­щади, видим, что образуется 4 участка напряжений.

Нормальные напряжения в сечениях по участкам:

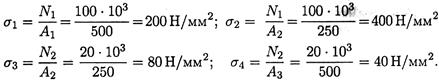
Откладываем значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.

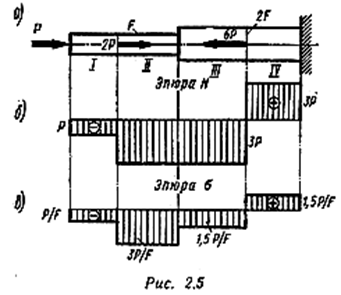
Пример 2. Для заданного бруса (рис. 2.5, а) построить эпюры продольных сил и нормальных напряжений.

Решение

Заданный брус имеет четыре участка I, II, III, IV (рис. 2.5, а). Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и места изменения размеров поперечного сечения.

Пользуясь методом сечений, строим эпюру продольных сил (рис. 2.5, б).

Для построения эпюры нормальных напряжений определяем их в поперечных сечениях каждого из участков:

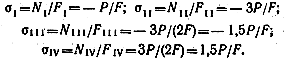
Эпюра σ представлена на рис. 2.5, в.

Пример 3. Определить количество деревянных стоек сечением 10x10 см, необходимых для поддержания, цистерны, вмещающей V = 40 м³ воды. Масса цистерны М_ц = 7,2-10³ кг. Допускаемое напряжение [σ] = 13 Н/мм³. При расчете считать, что усилия в стойках одинаковы.

Решение

Требуемая площадь поперечного сечения стоек

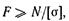
где 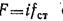(f_ст — площадь поперечного сечения одной стойки; i — число стоек);

N — усилие, передающееся на стойки.

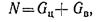
где Gц — сила тяжести цистерны; Gц = gт_ц = 9,81 * 7,2*10³ =70,7*10³ Н; G_в — сила тяжести воды; G_в = уV = 10*40 = 400 кН (у = 10 кН/м³ — объемная сила тяжести воды). Подставляя числовые значения, получаем

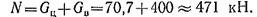
Тогда

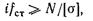
откуда находим требуемое число стоек:

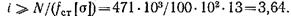
Принимаем i = 4.

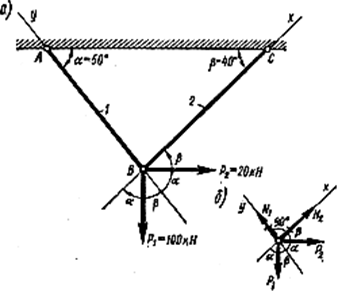
Пример 4. Для заданной стержневой системы (рис. 2.6, а) определить из расчета на прочность требуемые площади сечения стержней и подобрать по ГОСТ 8509—72 соответствующий номер угловой равнополочной стали, учитывая, что каждый стержень изготовлен из двух равнополочных уголков.

Для принятых сечений стержней определить расчет­ные напряжения н указать расхождения (в процентах) с допускаемым значением напряжения [σ] = 160 Н/мм³.

Решение

Здесь требуется подобрать сечения стержней исходя из условий:

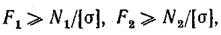
где N₁ и N₂ — усилия, возникающие соответственно в стерж­нях 1 и 2.

1. Усилия N₁ и N₂ во всех поперечных сечениях стерж­ней одинаковы и площади этих сечений постоянны. Таким образом, все сечения каждого стержня равноопасны.

2. Определяем усилия в стержнях из рассмотрения равно­весия узла В, где приложены заданные силы Р₁ и Р₂ (рис. 2.6, б). Освобождаем эту точку от связей и прикла­дываем их реакции N₁ и N₂, равные усилиям в стерж­нях. Получаем плоскую систему сходящихся сил. Для упрощения уравнений равновесия координатные оси ху направляем вдоль неизвестных усилий N₁ и N₂. Состав­ляем уравнения равновесия:

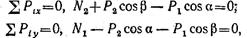
Откуда

Тогда

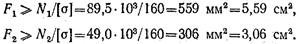
По таблицам ГОСТ 8509—72 подбираем сечения стерж­ней:

для первого стержня угловую равнополочную сталь 36x36x4

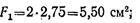
для второго стержня угловую равнополочную сталь 28x28x3

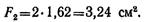
Вычислим напряжения в поперечных сечениях стерж­ней при принятых площадях

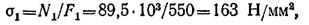
что больше [σ] на

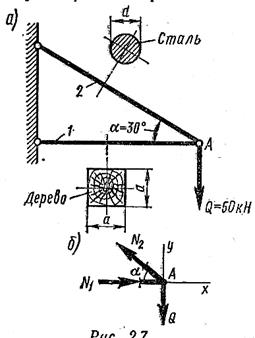
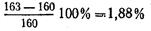
такое превышение допустимо;

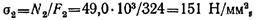
что меньше [σ] на

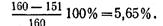
Пример 5. Определить размеры поперечных сече­ний стержней (рис. 2.7, а), если допускаемые напря­жения для стали [σ_сх] = 140 Н/мм², для дерева [σ_д] = 13 Н/мм².

Решение

Рассматри­ваем равновесие шарни­ра А, так как к этому шарниру приложены за­данная нагрузка и иско­мые усилия в стержнях.

1. Освобождаем шарнир А от связей и заменяем их действие реакциями N₁ и N₂. Действующие на шарнир А нагрузка и ис­комые усилия показаны на рис. 2.7, б. Получили плоскую систему сходящихся сил, которая находится в равновесии.

2. Выбираем систему координат и составляем уравнения равновесия:

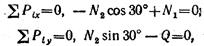
откуда

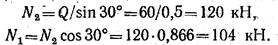
Требуемые площади поперечных сечений стержней

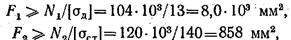
Откуда

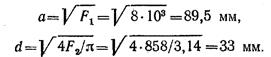
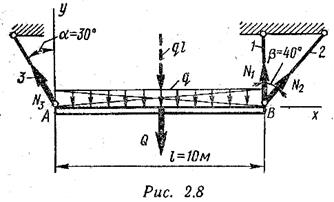Пример 6. Однородная балка АВ поддерживается тремя стальными стержнями1, 2, 3 круглого поперечного сечения d = 20 мм (рис. 2.8). Сила тя­жести балки Q = 10 кН. Найти до­пускаемую интенсив­ность [q] равномерно распределенной на­грузки, если допус­каемое напряжение для материала стерж­ней [σ] =160 Н/мм².

Решение

1. Определим усилия, возникающие в стержнях. Под действием силы Q, равномерно распределенной на­грузки q и усилий N₁, N₂ и N₃ в стержнях балка нахо­дится в равновесии.

2. Составляем уравнения равновесия:

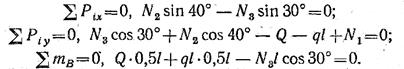
3. Решая полученные уравнения, находим:

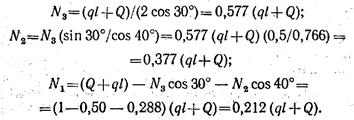
N₃ больше, чем N₁ и N₂. Следовательно, опасными являются поперечные сечения стержня 3.

4. Условие прочности для стержня 3:

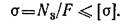
Подставляем значение N₃:

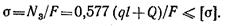
5. Решая относительно ц и подставляя числовые значе­ния, получаем:

где

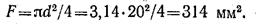
Пример 7. Стальной стержень круглого сечения диаметром d = 20 мм растягивается силой Р = 65 кН. Проверить прочность стержня, если его предел текучести σ = σ_т = 300 Н/мм² и требуемый коэффициент запаса [n] = 1,5.

Решение

Напряжения, возникающие в поперечном сечении стержня,

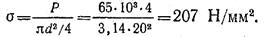
Расчетный коэффициент запаса

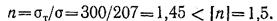
Следовательно, можно считать, что прочность стержня достаточна, так как расчетный коэффициент запаса незначительно (на 3%) меньше требуемого.

Контрольные вопросы и задания

1. Какие внутренние силовые факторы возникают в сечении бру­са при растяжении и сжатии?
2. Как распределяются по сечению силы упругости при растя­жении и сжатии? (Использовать гипотезу плоских сечений.)
3. Какого характера напряжения возникают в поперечном сече­нии при растяжении и сжатии: нормальные или касательные?
4. Как распределены напряжения по сечению при растяжении и сжатии?
5. Запишите формулу для расчета нормальных напряжений при растяжении и сжатии.
6. Как назначаются знаки продольной силы и нормального на­пряжения?
7. Что показывает эпюра продольной силы?
8. Как изменится величина напряжения, если площадь попереч­ного сечения возрастет в 4 раза?
9. В каких единицах измеряется напряжение?

ЛЕКЦИЯ 21