Частотный критерий устойчивости Найквиста.

Данный критерий применяется при анализе устойчивости замкнутой системы. Предположим, что разомкнутая система устойчива. Тогда для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики 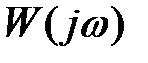разомкнутой системы не охватывал точку с координатами (–1, j0) на комплексной плоскости.

Частота, на которой 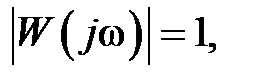называется частотой среза (w_ср). Величина 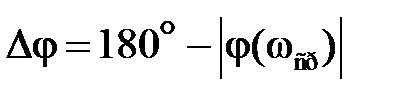называется запасом устойчивости по фазе(рис. 2.1). Рассматривают также запас устойчивости по модулю (по амплитуде) :

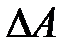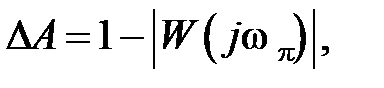(2.4)

где частота w_p определяется из соотношения:

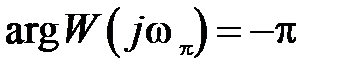. (2.5)

Рис. 2.1 Определение запасов устойчивости по АФЧХ

Из критерия Найквиста следует, что устойчивая вразомкнутом состоянии система будет устойчивой и в замкнутомсостоянии,если сдвиг по фазе на частоте среза не достигает –π(–180^°). Выполнение этого условия принято называть критерием устойчивости Найквиста для ЛАЧХ.

По логарифмическим частотным характеристикам разомкнутой САУ достаточно просто определяются также запасы устойчивости по амплитуде –∆L и по фазе -Δj (рис. 2.2).

В пакете Simulink возможно автоматическое применение трех критериев

устойчивости:

1) по корням характеристического уравнения системы;

2) частотные критерии устойчивости Найквиста;

3) критерий устойчивости Никольса.

Чаще применяются в основном первые два.

Устойчивость системы по корням характеристическогоуравнения определяется с использованием пакета расширения LTI Viewer.

Рис. 2.2Определение запасов устойчивости по ЛАЧХ

LTI Viewer может быть вызван следующим образом:

1) ВыполнитькомандуTools\LinearAnalysis… окнаSimulink–модели. В результате выполнения команды откроется окно Model_Inputs_and_Outputs (рис. 2.3), а также пустое окно Simulink LTI-Viewer;

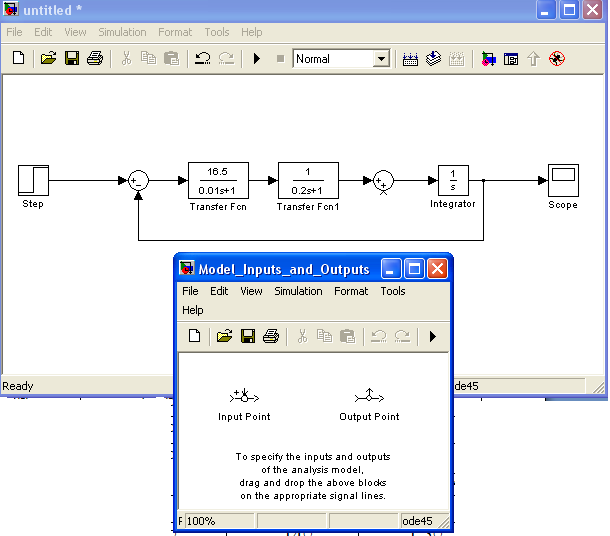
Рис.2.3 Исследуемая модель и окно Model_Inputs_and_Outputs

2) установить блок InputPoint на входе и блок OutputPoint на выход исследуемой системы (рис. 2.4);

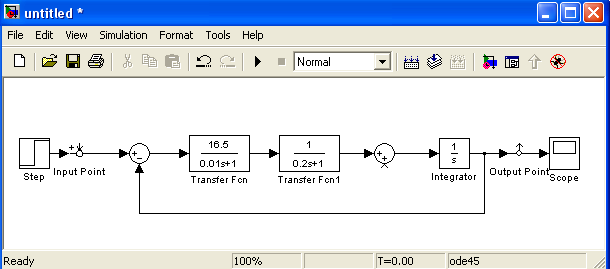
Рис.2.4 Исследуемая модель с установленными блокамиInputиOutput

3) вокне LTI-Viewer выполнитькомандуSimulink\Get Linearized Model. Данная команда выполняет линеаризацию модели и строит реакцию системы на единичное ступенчатое воздействие;

4) Для получения характеристик необходимо выполнить команду
Edit\PlotConfiguration…. В результате выполнения этой команды откроется окно, показанное на рис. 2.5.

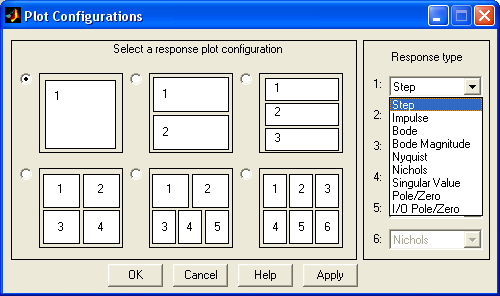
Рис.2.5 Окно PlotConfiguration

В данном окне можно выбрать число отображаемых графиков и вид отображаемых графиков.

Устойчивость системы по корням характеристическогоуравнения определяется выбором в поле Responsetypeвид графика для представления расположения нулей и полюсов замкнутой системы Pole/Zero.

Устойчивость системы по критерию Найквиста определяется с использованием пакета расширения LTI Viewer:

1) дляАФЧХ: Plot Type>Nyquist;

2) дляЛЧХ: Plot Type>Bode .

Для определения запасов устойчивости необходимо выбрать пунктконтекстного меню Characteristics>StabilityMargins(рис.2.6).

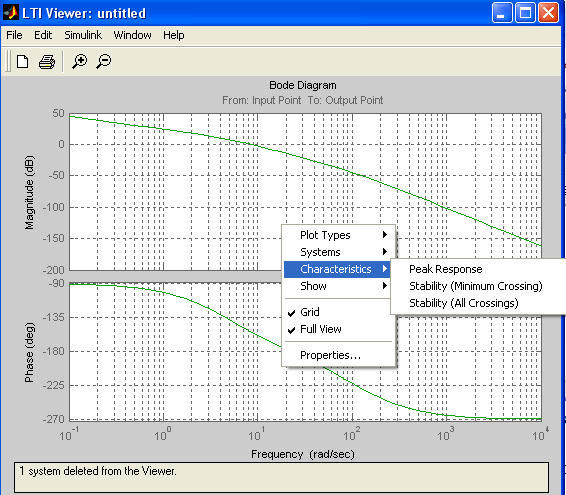
Рис.2.6 Определение запасов устойчивости

При этом в появляющихся окошках указаны численные значения запасов и частота в соответствующих точках логарифмических частотныххарактеристик:

–Gainmargin (dB) – запас устойчивости по амплитуде, дБ;

–Phasemargin (deg) – запас устойчивости по фазе, градусы;

–Atfrequency (rad/sec) – “начастоте”, рад/с.

2.2 Порядок выполнения работы

Структурная схема линейной САУ представлена на рис. 2.7.

Рис. 2.7 Структурная схема линейной системы

Соответствующие передаточные функции имеют вид:

; ;

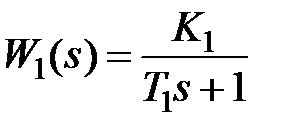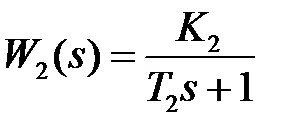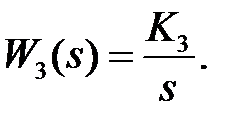
Параметры 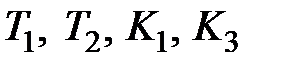для каждого варианта задания представлены в табл. 2.1.

Величина коэффициента 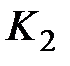на начальном этапе принять равной 1. Вдальнейшем будет выбираться из условия устойчивости.

1. Записать передаточные функции разомкнутой и замкнутой систем: 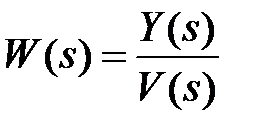при 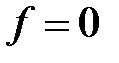, 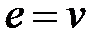(т. е. разомкнута главная обратная связь); 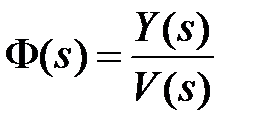при 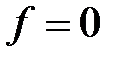- главная передаточная функция замкнутой системы. Задать их в командном окне пакета Matlab.

2. Используя критерий Гурвица, записать в общем виде условия устойчивости. При заданных в табл. 2.1 параметрах 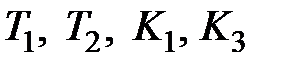найти граничное значение коэффициента передачи 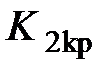, при котором система находиться на границе устойчивости. В дальнейшем полагать .

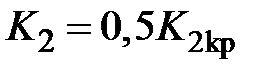3. Построить область устойчивости системы в плоскости общего коэффициента передачи 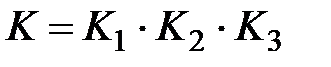и постоянной времени 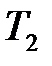при заданном значении 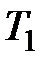. Найти граничное значение 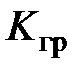при заданном значении 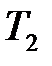, при котором система выходит на границу устойчивости.

4. Проанализировать устойчивость системы по критерию Найквистапри различных значениях коэффициента K, приняв его равным 0,5K_гр, K_гр, 5K_гр.

5. Набрать модель исследуемой системы в инструментальной среде моделирования Simulink, полагая 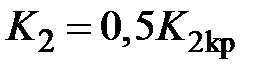. Получить переходные процессы в системе при заданных параметрах. Экспериментально определить критическое значение коэффициента передачи 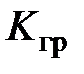, т.е. такое значение, при котором система находится на границе устойчивости.

6. Получить переходные процессы в системе при различных значениях коэффициента K, приняв его равным , .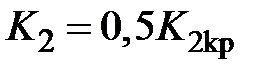

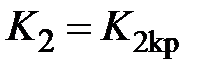7. Установив в схеме блоки входа(InputPoint) и выхода(OutputPoint) из библиотеки ControlSystemToolbox, при помощи встроенного инструмента просмотра – LTI-Viewer получитьграфик нулей и полюсов замкнутой системы. Исследовать влияние коэффициента усиления системы на расположение корней характеристического уравнения. Сделать вывод.

8. При помощи встроенного инструмента просмотра – LTI-Viewer, получить ЛАЧХ разомкнутой системы.Определить запасы устойчивости системы пр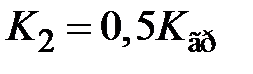и и .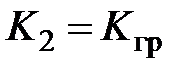

Таблица 2.1

Варианты заданий

Номер варианта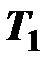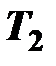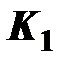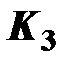
	0,01	0,2	16,5
	0,02	0,3		1,1
	0,03	0,4	15,5	1,2
	0,04	0,5		1,3
	0,05	0,6	14,5	1,4
	0,06	0,7		1,5
	0,07	0,8	13,5	1,6
	0,08	0,9		1,7
	0,09		12,5	1,8
	0,05	1,1		1,9
	0,06	1,2	0,2	11,5
	0,07	1,3	0,25
	0,08	1,4	0,3	10,5
	0,09	1,5	0,35
	0,1	1,6	0,4	9,5

2.3 Содержание отчета

1. Цель работы.

2.Структурная схема исследуемой системы и численные значения параметров.

3.Рассчитанные и экспериментально найденные критические значения параметров.

4. График переходных процессов исследуемой системы.

5. График зависимости K_гр(T₂).

2.4 Контрольные вопросы

1. Как формулируется основное условие устойчивости линейных систем?

2. Как по АФХ исследуемой разомкнутой системы найти k_1кр?

3. Как, используя критерий Гурвица для замкнутой системы, найти критическое значение коэффициента разомкнутой системы?

4.Какой вид имеет переходная характеристика системы, находящейся на колебательной границе устойчивости?

5.Каковы условия положения системы на границе устойчивости по критериям Гурвица, Михайлова, Найквиста?

Лабораторная работа №3
КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ

Цель работы:

- изучение основных качественных показателей системы в переходном и установившемся режимах

- определения статической и астатической ошибок САУ.

3.1Основные теоретические сведения

Численные величины, характеризующие работу системы автоматического управления, носят название показателей качества, которые условно можно разделить на три группы:

а) показатели качества, характеризующие устойчивость системы;

б) показатели качества, характеризующие точность системы;

в) показатели качества, характеризующие качество переходных процессов.

Обеспечение устойчивости является необходимым условием функционирования любой системы управления и гарантирует затухание свободной или переходной составляющей процесса.

К этой первой группе показателей относятся запасы устойчивости по амплитуде 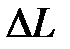и фазе .

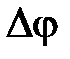После затухания свободной составляющей через достаточно большой промежуток времени в системе протекает установившийся процесс, который обуславливает точность системы. Показателями качества в данном случае выступают величины ошибок в установившемся режиме.

К третьей группе относятся показатели качества переходного процесса, которые характеризуют вид процесса для достаточно малых моментов времени после его начала. Эти показатели могут быть вычислены двумя способами. Первый – непосредственно по виду переходного процесса. В этом случае их называют прямыми оценками качества. Второй способ – это использование косвенных оценок показателей качества без построения кривой переходного процесса[].

На рис. 3.1 представлен наиболее распространенный вид переходной характеристики h(t).Для оценки качества регулирования по виду h(t) вводят следующие показатели качества:

t_р – время регулирования (время переходного процесса), это время, после которого величина 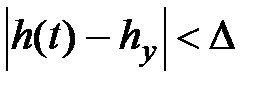, где обычно величина ;

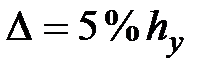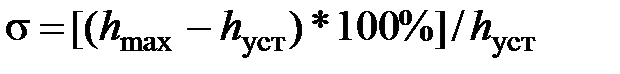–перерегулирование в процентах;

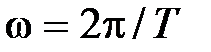– частота колебаний переходного процесса;

M – число колебаний за время переходного процесса.

Рис. 3.1

Наиболее важными показателями качества являются t_р и . Величина t_р может изменяться в широких пределах в зависимости от вида системы управления.

Перерегулирование обычно лежит в пределах от 0 до 30%. Число колебаний за время регулирования обычно 1 – 2, а иногда 3 – 4. В некоторых случаях колебания недопустимы.

По виду функции h(t) процессы делятся на три категории (рис. 3.2):
монотонные (1), апериодические (2)и колебательные (3).

Рис.3.2 Виды переходных процессов САУ

К косвенным оценкам качества относятся корневые оценки качества, интегральные оценки качества и частотные оценки.

Корни характеристического уравнения несут всю информацию о системе.По положению корней характеристического уравнения определяют:

– степень устойчивости;

– приближенно время переходного процесса;

– показатель колебательности в системе.

Степенью устойчивости η называется наименьшее из абсолютных значений вещественных частей корней характеристического уравнения

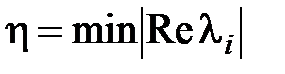, (3.1)

где 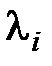– корни характеристического уравнения.

На комплексной плоскости – это расстояние от мнимой оси до ближайшего к ней корня или пары комплексно-сопряженных корней (рис. 3.3).

Рис. 3.3 Определение степени устойчивости

Связи между временем регулирования и степенью устойчивости имеет вид

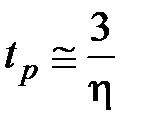. (3.2)

Величина 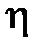характеризуют предельноебыстродействиесистемы, поэтомуиногдавеличину 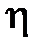называютещемеройбыстродействиясистемы.Доминирующеевлияниена характерпереходногопроцессаоказываютближайшиекмнимой оси корни.Если ближайшими являются комплексно-сопряженные корни 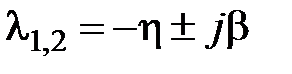, то наряду со степенью устойчивости вводят в рассмотрение колебательность системы (колебательность переходного процесса) .

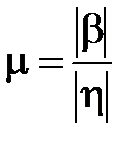Возможна оценка качественных показателей системы по виду логарифмических частотных характеристик разомкнутой системы. Всю характеристику можно условно разбить по оси частот на три диапазона, как это показано на рис. 3.4, где НЧ – диапазон низких частот, СЧ – средних и ВЧ – высоких частот.

Рис. 3.4 Области ЛАЧХ

Логарифмическая характеристика 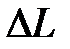в диапазоне НЧ влияет на точностные характеристики системы, так как первая асимптота определяется двумя величинами: К – коэффициентом усиления разомкнутой системы и 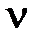– порядком астатизма. Область средних частот вблизи частоты среза 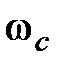в значительной степени определяет такие показатели системы, как запасы устойчивости 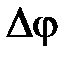, , 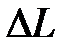время регулирования , перерегулирование , величину показателя колебательностиМ.

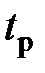Перерегулирование, запас устойчивости по фазе и показатель колебательности характеризуют колебательные свойства системы и связаны между собой приближенными соотношениями:

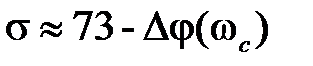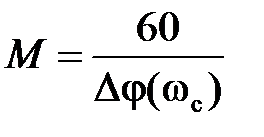; . (3.3)

Для определенного вида систем справедлива обратно пропорциональная зависимость времени переходного процесса и частоты среза:

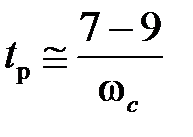. (3.4)

Структурная схема САУ с единичной обратной связью представлена на рис.3.5.

Рис. 3.5

Точность САУ по отношению к задающему воздействию характеризуется величиной ошибки управления

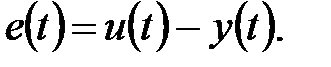(3.5)

Если 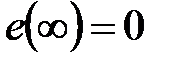, система называется астатическойпо отношению к задающему воздействию, в противном случае САУ -статическая.Величину e(t) можно оценить, зная передаточную функцию САУ по отношению к ошибке:

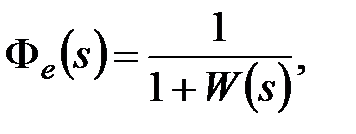(3.6)

где 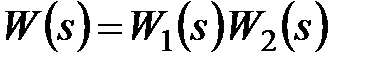– передаточная функция разомкнутой системы.

Для астатической САУ передаточная функция имеет вид

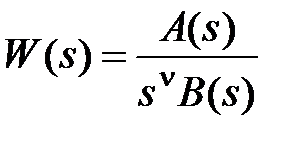, (3.7)

где 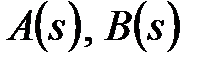-полиномы, а 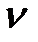- порядок астатизма.

Для статической САУ 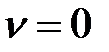при входном сигнале вида 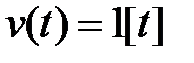величина статической ошибки 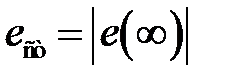определяется равенством

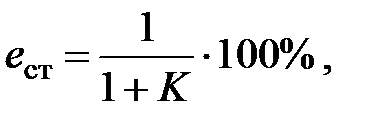(3.8)

где K- коэффициент усиления разомкнутой системы.

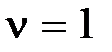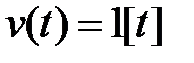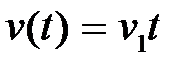При (система с астатизмом первого порядка) при воздействияхвида и величина ошибки соответственно для первого и второго типов входного сигнала определяется по формулам

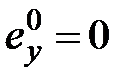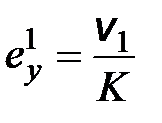, , (3.9)

где ошибку 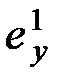будем называть ошибкой по скорости (скоростной ошибкой).

На рис. 3.6 показаны переходные процессы в различных системах при отработке скачка по положению и скорости: кривая 1 – для статической системы, 2 – для системы с астатизмом первого порядка, 3 – для системы с астатизмом второго порядка.

Рис. 3.6.

Точность САУ по отношению к возмущающему воздействиюf(t)можно оценить, используя соответствующую передаточную функцию по возмущению:

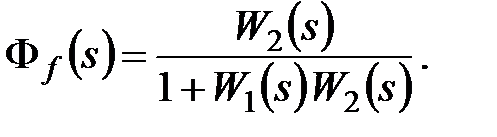(3.10)

Порядок астатизма системы по отношению к возмущению определяется числом интегрирующих звеньев, расположенных на структурной схеме до точки приложения возмущения и не охваченных местными обратными связями.

Выражение для ошибки в исследуемой системе (рис.3.7) имеет вид

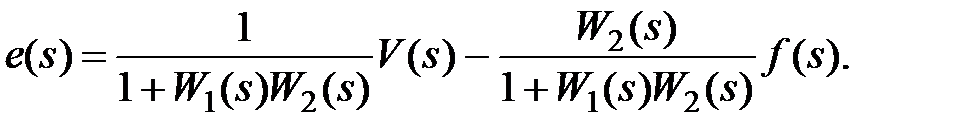
При u(t)=const,f(t)=constможно найти статическую ошибку

.

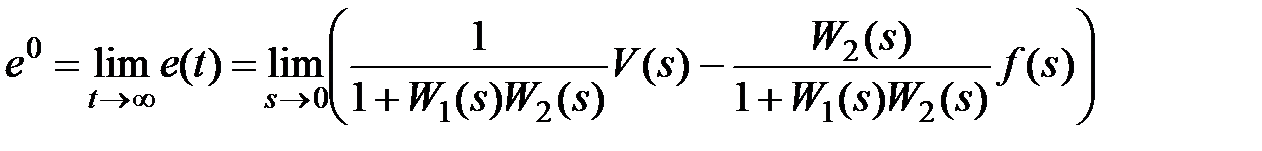В статической системе ошибка 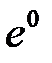не равна нулю, и её абсолютная величина определяется значениями v и f, а также коэффициентом усиления разомкнутой системы: чем он больше, тем меньше ошибка. Однако необходимо помнить, что с увеличением коэффициента усиления уменьшается запас устойчивости системы, т.е. требования точности и устойчивости оказываются противоречивыми.
В астатической системе составляющая ошибки 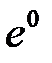от действия v=const всегда будет равна нулю, а от f=const обращается в ноль только в том случае, когда точка приложения возмущения «расположена» после интегратора.

3.2 Порядок выполнения работы

Структурная схема исследуемой системы автоматического управления приведена на рис. 3.7.

Рис. 3.7

Соответствующие передаточные функции имеют вид:

; ;

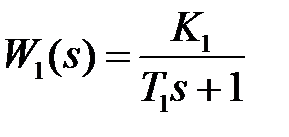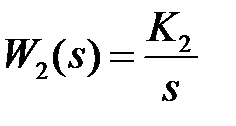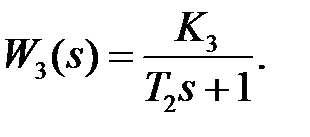
Параметры 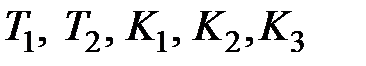для каждого варианта задания представлены в табл. 3.1.

На вход системы скачком подается задающее воздействие 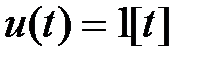. Также имеются возмущающие воздействия 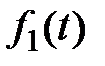и 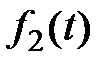, приложенные в разных точках прямого канала системы.

1.В соответствии с вариантом задания (см. таблицу 3.1) необходимо собрать цифровую модель исследуемой системы в пакетеMatlab/Simulink. Подайте на вход модели ступенчатое воздействие 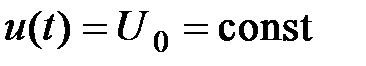в соответствии с номером варианта, возмущающие воздействия следует отключить. Получить с помощью осциллографа Scope переходную характеристику САУ h(t). Определить прямые показатели качества.

2. Получить графики расположения корней характеристического уравнения, используя LTI-Viewer. Определить косвенные оценки качества.

3.Повторить пункты 1и 2 при удвоенном значении входного сигнала. Сделать вывод о зависимости показателей качества от величины задающего воздействия.

4. Получить графики переходного процесса, расположения корней характеристического полинома при уменьшенном и увеличенном значении коэффициента усиленияK₁, а именно K₁=1,75 и K₁=7. Определить прямые и косвенные показатели качества. Сделать вывод о влиянии коэффициента усиления на показатели качества процесса управления.

5.Получить графики переходного процесса, расположения корней характеристического полинома для следующих значений постоянной времениT₁, а именно T₁=0,17 c и T₁=0.25. Определить прямые и косвенные показатели качества. Сделать вывод о влиянии постоянной времени на показатели качества процесса управления. Построить ЛАЧХ и ЛФЧХ разомкнутой системы для заданного изменения значения T₁ и определить запасы устойчивости по амплитуде и фазе.

6. Определить показатели качества процесса управления относительно возмущающих воздействий. Снять графики e(t),y(t)при

а)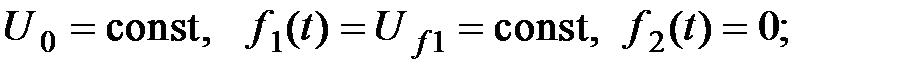

б)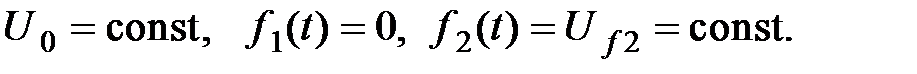

7. Определить прямые показатели качества процесса управления. Рассчитать установившиеся ошибки и сравнить их с определенными путем моделирования. Сделать вывод о порядке астатизма системы по отношения к входному и возмущающим воздействиям.

Таблица 3.1

Параметры передаточных функций

Параметр
К1	3,5			3,8	3,5	5,2	4,8
K2
K3
T1,c	0,7	0,7	0,7	0,7	0,7	0,7	0,7	0,7
T2,c	0,1	0,1	0,1	0,1	0,1	0,1	0,1	0,1
U0		1,5		2,5		3,5		4,5
Uf1						2,5
Uf2						2,5
Параметр
К1		3,5	4,2	5,3	3,2		5,4	3,8
K2
K3
T1,c	0,7	0,7	0,7	0,7	0,7	0,7	0,7	0,7
T2,c	0,1	0,1	0,1	0,1	0,1	0,1	0,1	0,1
U0						2,5
Uf1						2.5
Uf2						2,5

3.3Содержание отчета

1. Цель работы.

2. Структурная схема системы управления и ее параметры;

3.Кривые переходных процессов, распределения корней и найденные по ним прямые и косвенные показатели качества;

4.Расчет статических ошибок;

5.Логарифмические частотные характеристики разомкнутой системы, запасы устойчивости;

6. Анализ результатов исследования по каждому пункту работы и общие выводы по работе.

3.4 Контрольные вопросы

1. Что понимают под качеством процесса управления?

2. Назовите показатели качества установившегося режима и переходного процесса.

3. Какие вы знаете оценки качества переходного процесса?

4. Чем отличаются прямые методы оценки качества переходного процесса от косвенных?

5. Как рассчитывается установившаяся ошибка относительно воздействия: а) задающего? б) возмущающего?

6. Какая система называется статической?Какая система называется астатической?

7. Как зависит точность системы от порядка ее астатизма?Как по структурной схеме определяется порядок астатизма системы?

8. Как влияет местоположение интегратора в системе на точность работы САУ по отношению к возмущающему воздействию?

9. Как оценивается качество переходного процесса с помощью АЧХ замкнутой системы?

10. Как оценивается качество переходного процесса с помощью ЛАЧХ разомкнутой системы?

ЛАБОРАТОРНАЯ РАБОТА №4
ИССЛЕДОВАНИЕ ПРИНЦИПОВ ПОСТРОЕНИЯ РЕГУЛЯТОРОВ

ЛИНЕЙНЫХ СИСТЕМ

Цель работы:

– исследование влияния введения управления по интегралу и производной от ошибки регулирования на точности и качество процессов управления линейных динамических систем.

4.1 Краткие теоретические сведения

Задача синтеза систем автоматического управления (коррекция ихдинамических свойств) состоит в выборе структуры и параметров системрегулирования объектами, которые в соответствии с заданными техническимиусловиями обеспечивают наиболее рациональные характеристики по запасамустойчивости и показателям качества.

Коррекция осуществляется с помощью введения в систему специальных корректирующих звеньев с особо подобранной передаточной функцией.Таким образом, задача синтеза включает в себя определение структуры ипараметров корректирующих звеньев при известных параметрах остальныхзвеньев, входящих в систему, с учетом заданных технических условий.

Корректирующие звенья могут включаться последовательно, параллельно

и в обратной связи. В непрерывных системах автоматического управления используется множество типов корректирующих устройств и в общем случае их структура может быть любой. Однако в теории автоматического управления выделяюттиповые корректирующие звенья, которые называются регуляторами [].

Типовые регуляторы являются наиболее универсальными и распространенными регуляторами. В силу своей универсальности они легко приспосабливаются для автоматизации разнообразных технологических процессов и объектов.

Типовые регуляторы реализуют типовые законы управления.

Закон управления – это алгоритм или функциональная зависимость, в соответствии с которыми регулятор формирует управляющее воздействие u(t).

Эта зависимость может быть представлена в виде:

u(t) = F(e,g,f),

где F– некоторый оператор от сигнала рассогласования e(t), задающего воздействия v(t) и возмущающего воздействия f(t), а также от их производных и интегралов по времени.

Обычно закон управления можно разделить по виду входного сигнала на три слагаемых:

u(t) = F₁(e) + F₂(v) + F₃(f),

где F₁(e), F₂(v) и F₃(f) – выражают управление по отклонению, задающему
и внешнему воздействиям, соответственно.

В зависимости от вида оператора F законы управления делятся настандартные и специальные:

–стандартные законы управления – это универсальные законы, с помощью которых можно решать задачи автоматизации разнообразных технологических процессов и объектов.

– специальные законы управления – это законы, формируемые для решения конкретных задач.

Стандартный закон управления имеет следующий вид:

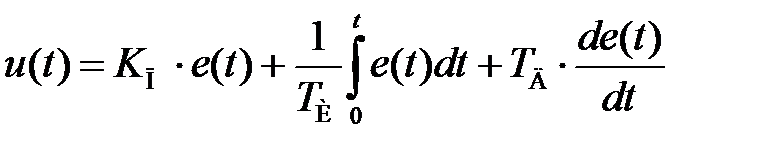(4.1)

Первое слагаемое является пропорциональной, второе – интегральной, третье – дифференциальной составляющими стандартного закона управления.

Коэффициенты K_П, T_ИиТ_Д определяют вклад каждой из составляющих в формируемое управляющее воздействие.

Регулятор, формирующий управляющее воздействие в соответствии со стандартным законом управления имеет передаточную функцию:

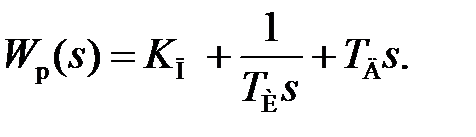(4.2)

Структура регулятора представлена на рис. 4.1.

Рис.4.1

Пропорциональная составляющаястандартного закона управления позволяет уменьшить установившуюся ошибку:

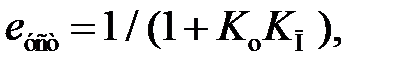
где K_о – коэффициент передачи объекта управления.

Интегральная составляющая стандартного закона управления вводится для повышения степени астатизма системы и, следовательно для повышения точности: e_уст = 0.

Дифференциальная составляющая стандартного закона управления непосредственно не влияет на установившуюся ошибку. Однако она повышает запас устойчивости системы, что позволяет компенсировать потерю устойчивости при увеличении вклада пропорциональной и интегрирующей составляющих.

Кроме того, дифференцирующая составляющая обеспечивает повышение быстродействия и снижение динамической ошибки системы, то есть работает с «предвидением» (предварением).

Рассмотрим типовые алгоритмы управления(законы регулирования), применяемые в линейных автоматических системах.

П (пропорциональный) – регулятор:

Простейший закон регулирования реализуется при помощи безынерционного звена с передаточной функцией

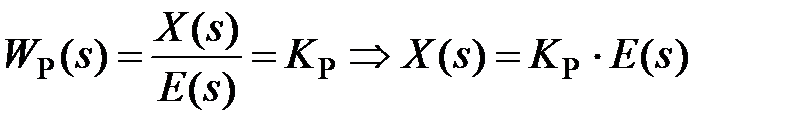. (4.3)

Согласно этому выражению, управляющее воздействие и в статике и в динамике пропорционально сигналу ошибки е. Поэтому такой закон регулирования называется пропорциональным (П).

Преимуществами данного регулятора являются простота и быстродействие, а недостатком – ограниченная точность.

И (интегральный) – регулятор:

Закон регулирования, которому соответствует передаточная функция

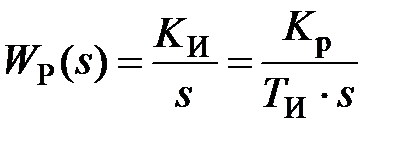, (4.4)

где K_р – коэффициент усиления регулятора;

Т_И – постоянная времени регулятора.

При интегральном управлении получается астатическая система.

Повышение степени астатизма приводит к увеличению установившейся точности системы, но одновременно снижает ее быстродействие, а также приводит к ухудшению устойчивости.

ПИ – регулятор:

Наибольшее распространение в промышленной автоматике получил пропорционально-интегральный(ПИ) закон регулирования

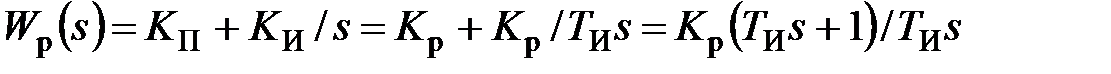. (4.5)

Пропорционально–интегральное (изодромное) управление сочетает в себе высокую точность интегрального управления (астатизм) с большим быстродействием пропорционального управления.

ПД – регулятор:

Наилучшее быстродействие достигается при пропорционально - дифференциальном (ПД) законе регулирования

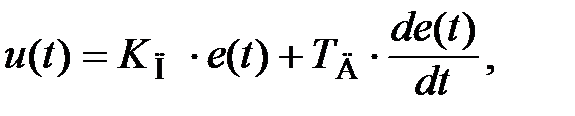
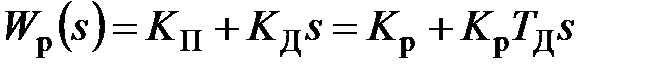. (4.6)

ПД – регулятор реагирует не только на величину сигнала ошибки, но и на скорость его изменения. Благодаря этому при управлении достигается эффект упреждения. Недостатком пропорционально – дифференциального закона регулирования является ограниченная точность.

Пропорционально-дифференциальное управление применяются для
повышения быстродействия работы системы. В результате увеличивается
скорость реакции системы, повышается быстродействие, снижается ошибка в динамике.

ПИД – регулятор:

Наиболее гибким законом регулирования (в классе линейных законов) является пропорционально – интегрально – дифференциальный(ПИД) закон

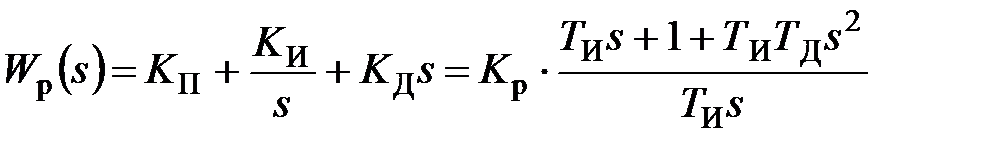, (4.7)

который сочетает в себе преимущества более простых законов.

ПИД–регулятор, представляющий собой астатический изодромный регулятор с предвидением, обеспечивает повышенную точность и повышенное быстродействие системы.

Настройка такого регулятора заключается в задании значений коэффициентов K_П, T_И, T_Д таким образом, чтобы удовлетворить требованиям качества управления в соответствии с выбранными критериями качества.

Существует инженерный подход к синтезу ПИД–регуляторов – методика Зиглера–Николса, которая предполагает следующиешаги:

1.Коэффициенты 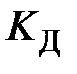и 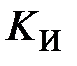устанавливаются равными нулю, а коэффициент 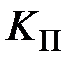увеличивается до тех пор, пока система не потеряет устойчивость.

2.Предельное значение 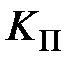обозначается как 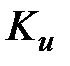, а период автоколебаний как .

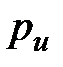3.Значения коэффициентов ПИД – регулятора рассчитываются последующим формулам:

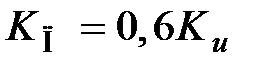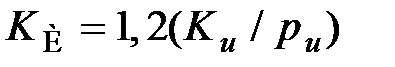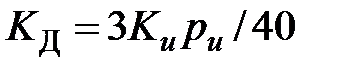, , . (6.3)

В аналоговых промышленных ПИД–регуляторах коэффициенты настраиваются вручную.

4.2 Порядок выполнения работы

На рис. 4.2 - 4.4 представлены схемы набора для исследования процессов регулирования объектами типа апериодическое звено 1-го порядка (рис.4.2) и двойного интегрирующего звена (рис.4.3 и 4.4).

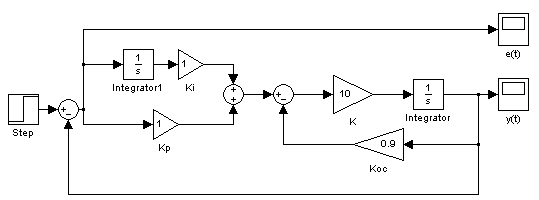
Рис. 4.2 Модель системы с ПИ-регулятором

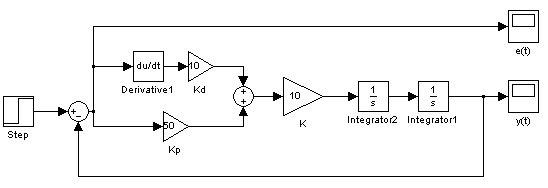
Рис. 4.3 Модель системы с ПД-регулятором

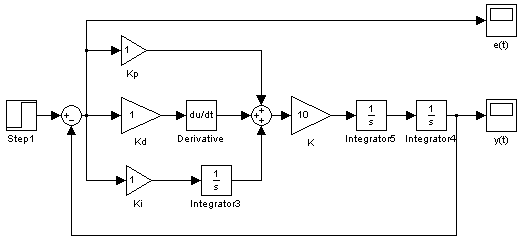
Рис. 4.4 Модель системы с ПИД-регулятором

Для исследования влияния структуры и параметров регулятора на процессы в системе необходимо поочередно рассмотреть САР с различными вариантами регуляторов – П, ПД, ПИ, ПИД при различных значениях коэффициентов передачи.

Порядок выполнения работы следующий:

1. Собрать модель замкнутой САР для апериодического звена 1-го порядка (рис.4.2) с параметрами, заданными в табл. 4.1. На вход системы подать сигнал 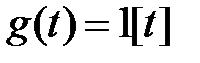. Зарисовать график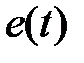и и 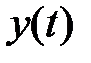исходной нескорректированной системы.

2. Исследовать влияние коэффициентов 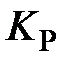и 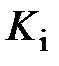на характер изменения функции 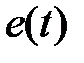. Для этого провести следующие эксперименты:

2.1. Установить 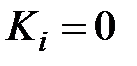. Меняя 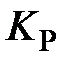определить зависимость статической ошибки, времени регулирования и перерегулирования от величины .

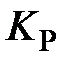2.2.Установить 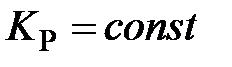. Меняя 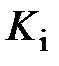оценить эффект от введения интегральной составляющей в закон управления. Зарисовать графики , .

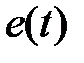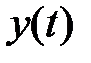По экспериментальным данным сделать выводы о в