Частотный критерий устойчивости Найквиста - Михайлова

Частотный критерий устойчивости, первоначально разработанный в 1932 г. американским ученным Найквистом для исследования усилителей с отрицательной обратной связью, был обоснован, обобщен и впервые применен в теории автоматического регулирования А.В. Михайловым.

Частотный критерий связывает свойства разомкнутой системы со свойствами замкнутой системы.

Физический смысл критерия устойчивости Найквиста-Михайлова состоит в том, что он позволяет по годографу АФХ разомкнутой системы судить об устойчивости замкнутой системы.

Рассмотрим функцию 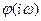, связанную с 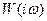соотношением:

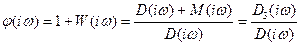(5-11)

Знаменатель этой функции представляет собой характеристическую кривую разомкнутой системы, а числитель – характеристическую кривую замкнутой системы.

Предположим, что разомкнутая система устойчива. Устойчивость разомкнутой системы можно установить без вычислений непосредственно по составу и характеристикам ее звеньев. Например, разомкнутая система, состоящая из устойчивых звеньев и не содержащая положительных обратных связей, заведомо устойчива.

Если разомкнутая система устойчива, то изменение аргумента 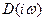при возрастании 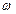от 0 до ∞ будет равно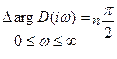

где 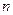- степень характеристического уравнения разомкнутой системы, совпадающая со степенью характеристического уравнения замкнутой системы. Это следует из того, что степень числителя передаточной функции 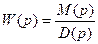в реальных системах не может превосходить степень знаменателя.

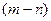Предположим, что характеристическое уравнение замкнутой системы имеет корней в правой части плоскости корней и, следовательно, корней в левой части комплексной плоскости корней 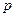. (Рис. 5.3)

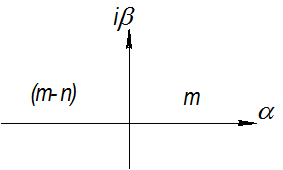
Рис. 5.3 Плоскость корней характеристического уравнения замкнутой системы.

Тогда при возрастании от 0 до ∞ изменение аргумента вектор 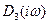будет равно

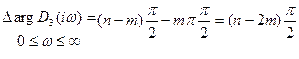. (5-13)

Изменение аргумента функции 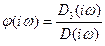при возрастании 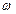от 0 до ∞ равно разности изменений аргумента 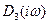- числителя функци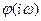и и 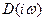-ее знаменателя, т.е. .

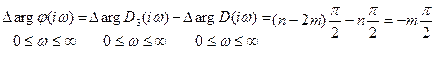Система устойчива, если корни ее характеристического уравнения в правой части комплексной плоскости корней отсутствуют, т.е. 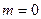, тогда ,

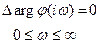Это означает, что вектор функции 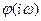на комплексной плоскости опишет угол, равный нулю лишь в том случае, если годограф вектора не охватывает начало координат комплексной плоскости. (Рис. 5.4,а)

Рис. 5.4 Амплитудо-фазовые характеристики.

Но от годографа 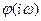легко перейти к годографу 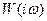, т.е. к АФХ разомкнутой системы, которая представляет ту же кривую, но сдвинутую на единицу влево. В комплексной плоскости 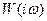начало координат находится в точке 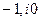, а конец вектора функции 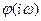при изменении скользит по АФХ разомкнутой системы. (Рис. 5.4,б)

Отсюда следует формулировка частотного критерия устойчивости: исследуемая замкнутая система, устойчивая в разомкнутом состоянии будет устойчива, если при изменении от 0 до ∞ АФХ разомкнутой системы в плоскости комплексного переменного 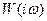не охватывает точку с координатами .

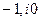При исследовании многоконтурных систем или систем, содержащих неустойчивые звенья, разомкнутая система может оказаться неустойчивой. Естественно, что для такой системы возможность экспериментального определения АФХ исключена, однако ее можно вычислить по уравнениям системы или передаточной функции и сделать заключение об устойчивости замкнутой системы.

В этом случае изменение аргумента 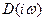при возрастании от 0 до ∞ будет равно

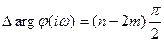, (5-14)

0 ≤ ≤ ∞

где - число корней характеристического уравнения разомкнутой системы 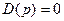, лежащих в правой части плоскости корней.

Если замкнутая система устойчива, то изменение аргумента 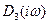будет

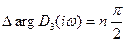(5-15)

0 ≤ ≤ ∞

Тогда 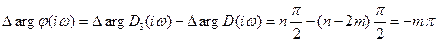(5-16)

0 ≤ ≤ ∞ 0 ≤ ≤ ∞ 0 ≤ ≤ ∞

Для этого случая частотный критерий устойчивости формулируется следующим образом.

Исследуемая система, неустойчивая в разомкнутом состоянии, будет устойчива в разомкнутом состоянии, если АФХ разомкнутой системы охватывает точку с координатами 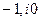в положительном направлении (против часовой стрелки) 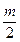раз.

Для астатических систем регулирования, содержащих, в частности, интегрирующие звенья, АФХ при 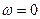обращается в бесконечность. Для подобных разомкнутых систем характеристическое уравнение имеет корни, лежащие в начале координат плоскости корней, т.е. корни равные нулю. (Рис. 5.5)

Рис. 5.5 Амплитудо-фазовая характеристика астатических систем регулирования..

В общем случае критерий устойивости Найквиста-Михайлова формируется так.

Замкнутая система будет устойчива, если разность между положительными и отрицательными переходами АФХ разомкнутой системы отрезка действительной оси (-∞,-1) равна 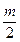раз, где - число корней с положительной вещественной частью характеристического уравнения разомкнутой системы.