Разбиение вероятностного пространства. Формула полной вероятности.

События образуют полную группу, если хотя бы одно из них обязательно произойдет в результате эксперимента и попарно несовместны.

Предположим, что событие A может наступить только вместе с одним из нескольких попарно несовместных событий , образующих полную группу. Будем называть события (i = 1, 2,…, n) гипотезами доопыта (априори). Вероятность появления события А определяется по формуле полной вероятности:

. (2.6)

Пример 16.Имеются три урны. В первой урне находятся 5 белых и 3 черных шара, во второй – 4 белых и 4 черных шара, а в третьей – 8 белых шаров. Наугад выбирается одна из урн (это может означать, например, что осуществляется выбор из вспомогательной урны, где находятся три шара с номерами 1, 2 и 3). Из этой урны наудачу извлекается шар. Какова вероятность того, что он окажется черным?

Решение. Событие A – извлечен черный шар. Если было бы известно, из какой урны извлекается шар, то искомую вероятность можно было бы вычислить по классическому определению вероятности. Введем предположения (гипотезы) относительно того, какая урна выбрана для извлечения шара.

Шар может быть извлечен или из первой урны (гипотеза ), или из второй (гипотеза ), или из третьей (гипотеза ). Так как имеются одинаковые шансы выбрать любую из урн, то .

Далее находим вероятности события A при каждой из гипотез:

Отсюда следует, что

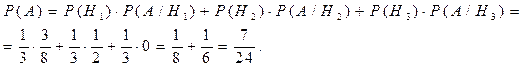
Пример 17.Электролампы изготавливаются на трех заводах. Первый завод производит 30 % общего количества электроламп, второй – 25 %,
а третий – остальную часть. Продукция первого завода содержит 1% бракованных электроламп, второго – 1,5 %, третьего – 2 %. В магазин поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине лампа оказалась бракованной?

Решение. Предположения необходимо ввести относительно того, на каком заводе была изготовлена электролампа. Зная это, мы сможем найти вероятность того, что она бракованная. Введем обозначения для событий: A – купленная электролампа оказалась бракованной, – лампа изготовлена первым заводом, – лампа изготовлена вторым заводом,
– лампа изготовлена третьим заводом.

Имеем: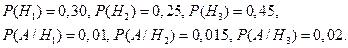

Искомую вероятность находим по формуле полной вероятности:

Формула Байеса.

Пусть – полная группа попарно несовместных событий (гипотезы). А – случайное событие. Тогда,

(2.7)

Последнюю формулу, позволяющей переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А, называют формулой Байеса.

Пример 18.В специализированную больницу поступают в среднем 50 % больных с заболеванием К, 30 % – c заболеванием L, 20 % –
с заболеванием M. Вероятность полного излечения болезни K равна 0,7 для болезней L и M эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что этот больной страдал заболеванием K.

Решение. Введем гипотезы: – больной страдал заболеванием К, – больной страдал заболеванием L, – больной страдал заболеванием M.

Тогда по условию задачи имеем . Введем событие А – больной, поступивший в больницу, был выписан здоровым. По условию

По формуле полной вероятности получаем:

По формуле Байеса .